Элементы комбинаторики

Основная формула комбинаторики

Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов.
Выберем по одному элементу из каждой группы. Тогда общее число N способов,
которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *…*n k .

Пример 1.
Поясним это правило на простом
примере. Пусть имеется две группы элементов, причем первая группа состоит из
n 1 элементов, а вторая — из n 2 элементов. Сколько
различных пар элементов можно составить из этих двух групп, таким образом,
чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли
первый элемент из первой группы и, не меняя его, перебрали все возможные
пары, меняя только элементы из второй группы. Таких пар для этого элемента
можно составить n 2 . Затем мы берем второй элемент из первой группы
и также составляем для него все возможные пары. Таких пар тоже будет n 2 .
Так как в первой группе всего n 1 элемент, всего возможных
вариантов будет n 1 *n 2 .

Пример 2.
Сколько
трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если
цифры могут повторяться?Решение:
n 1 =6
(т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7
(т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5,
6), n 3 =4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.

В том случае, когда все группы состоят из одинакового числа элементов, т.е. n 1 =n 2 =…n k =n
можно считать, что каждый выбор производится из одной и той же группы, причем
элемент после выбора снова возвращается в группу. Тогда число всех способов
выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.

Пример 3.
Сколько всех четырехзначных чисел
можно составить из цифр 1, 5, 6, 7, 8?Решение.
Для каждого разряда
четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.

Рассмотрим множество, состоящие из n элементов. Это
множество в комбинаторике называется генеральной
совокупностью
.

Расчет комбинаций чисел с повторениями

Комбинаторика – вычислительная область, занимающаяся изучением комбинаторных структур и способов их построения. Расчет комбинаций чисел с повторениями – одна из важных задач этой области.

Числа с повторениями в комбинаторике – это числа, которые состоят из ограниченного набора цифр и могут содержать повторяющиеся элементы. Например, число 53577 имеет две одинаковые цифры 5.

Для расчета комбинаций чисел с повторениями можно использовать различные методы. Один из них заключается в использовании формулы комбинаторики:

C_nk = (n + k — 1)! / (k!(n — 1)!)

Где:

C_nk – количество комбинаций чисел с повторениями;
n – количество различных элементов, из которых строится комбинация;
k – длина комбинации;
! – факториал числа.

Пример расчета комбинаций чисел с повторениями:

Пусть имеется набор из трех различных цифр {1, 2, 3}.
Необходимо вычислить количество различных двухзначных чисел, которые можно составить из этого набора чисел.
Используя формулу, получаем: C₃2 = (3 + 2 — 1)! / (2!(3 — 1)!) = 4.
Таким образом, из набора {1, 2, 3} можно составить 4 различных двухзначных числа с повторениями.

Расчет комбинаций чисел с повторениями широко применяется в различных областях, включая математическую статистику, теорию вероятности, компьютерные науки и др. Этот метод позволяет анализировать и моделировать различные ситуации, где необходимо учесть возможное повторение элементов в комбинациях чисел.

Сколько существует трехзначных чисел, подходящих под условия делимости?

Сколько существует положительных трехзначных чисел: а) не делящихся ни на одно из чисел 3, 8, 20? б)делящихся ровно на одно из этих трех чисел?

94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 Ответы с готовыми решениями:

Определить, сколько существует натуральных чисел N, подходящих под данное условиеСколько существует натуральных чисел N со следующим свойством: если к числу N справа приписать.

Сколько существует натуральных трехзначных чиселСколько существует натуральных трехзначных чисел, составленных из трех различных цифр 1 ,3, 5 ?

Сколько существует положительных трехзначных чиселСколько существует положительных трехзначных чисел: а) делящихся на числа 6, 15 или 25? б).

Сколько существует трехзначных чисел, которые делятся на 3 без остаткаСколько существует трехзначных чисел, составленных из цифр 1, 2, 3, 4, 5 и 6 (цифры могут.

4057 / 3021 / 913 Регистрация: 19.11.2012 Сообщений: 6,160

Сообщение от RumeOne

не делящихся ни на одно

[900/3]=300 штук делятся на 3, [900/8]=112 штук делятся на 8, [900/20]=45 штук делятся на 20, [900/24]=37 штук делятся на 24=НОК(3,8), [900/60]=15 штук делятся на 60=НОК(3,20), [900/40]=22 штук делятся на 40=НОК(8,20), 900/120=7 штук делятся на 120=НОК(3,8,20) Заполняйте оставшиеся места на картинке и получайте ответы на все вопросы. По-моему, используя информацию указанную выше, с такой задачей справится ученик только что научившийся считать до 1000.

Кликните здесь для просмотра всего текста

10072 / 6657 / 3610 Регистрация: 14.01.2014 Сообщений: 15,376 Не совсем верно: должно быть 113, 23 и 8. Регистрация: 15.12.2018 Сообщений: 222 С 8 соглашусь. Но 112 и 22 правильно

10072 / 6657 / 3610 Регистрация: 14.01.2014 Сообщений: 15,376 Согласен. Ответ на пункт: а) 509 остался тот же самый.

4057 / 3021 / 913 Регистрация: 19.11.2012 Сообщений: 6,160

Сообщение от RumeOne

С 8 соглашусь

Да, замечания совершенно справедливые. Формула должна быть такой (начну с конца): [999/120]-[99/120]=8, [999/40]-[99/40]=22 и т.д.

Регистрация: 15.12.2018 Сообщений: 222

А можно уточнить как получилось 509? Просто у меня 443. Решал вот так: Всего трехзначных чисел 900. Из них делящихся на 3 – 300, на 8 -112, на 20 — 45, на 3 и 8 – 37, на 3 и 20 – 15, на 8 и 20 – 22, на 3, 8 и 20 – 8. Таким образом, чисел, которые не делятся ни на 3, ни на 8, ни на 20 = 900-300-112-45=443.

10072 / 6657 / 3610 Регистрация: 14.01.2014 Сообщений: 15,376

По формуле включений-исключений чисел, делящихся на 3, 8 и 20, будет 300+112+45-37-15-22+8=391. Оставшихся чисел 900-391=509.

87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604Помогаю со студенческими работами здесь

Сколько существует трехзначных чисел, в которых все цифры четные и разные?Сколько существует трехзначных чисел, в которых все цифры четные и разные?

Сколько существует трехзначных чисел, в которых все цифры нечетные и разные?Сколько существует трехзначных чисел, в которых все цифры нечетные и разные?

Сколько существует трехзначных чисел, в записи которых встречается один раз цифра 2Поиогите решить эти задачи на языке паскаль: 2. Сколь существует трехзначных чисел в записи.

Сколько существует трехзначных натуральных чисел, у которых хотя бы одна из цифр делится на 5?Помогите пожалуйста Сколько существует трехзначных натуральных чисел у которых хотя бы одна из.

Сколько существует восьмеричных трёхзначных чисел, в каждом из которых чётные и нечётные цифры чередуютсяПомогите пожалуйста решить задачу. Сколько существует восьмиричных трёхзначных чисел, в каждом из.

Рассчет числа возможных комбинаций

Сколько может быть комбинаций из трех цифр? Для ответа на этот вопрос нам необходимо учесть, что каждая из трех позиций в комбинации может быть заполнена любой из десяти цифр: от 0 до 9. Таким образом, количество возможных комбинаций можно рассчитать как произведение количества вариантов для каждой позиции.

В данном случае каждая позиция может принимать 10 различных значений, поэтому для первой позиции имеем 10 вариантов выбора. Для второй позиции также 10 вариантов, и для третьей позиции также 10 вариантов. Таким образом, общее число возможных комбинаций равно произведению этих трех чисел:

Сколько может быть комбинаций из трех цифр?

Количество комбинаций равно 10 x 10 x 10 = 1000.

Таким образом, из трех цифр может быть 1000 комбинаций. Каждая комбинация представляет собой уникальную последовательность из трех цифр.

Сколько различных цифр можно использовать?

Если речь идёт о составлении комбинаций из трех цифр, то можно использовать любые цифры от 0 до 9. Таким образом, на каждую позицию в комбинации может быть выбрана любая из 10 цифр. Учитывая, что комбинация состоит из трех позиций, общее количество комбинаций можно рассчитать по формуле:

количество комбинаций = количество цифрколичество позиций = 103 = 1000

Таким образом, количество возможных комбинаций из трех цифр составляет 1000.

Влияет ли порядок на комбинации из трех цифр?

Когда речь идет о комбинациях из трех цифр, порядок играет важную роль. Представим, что у нас есть три цифры: 1, 2 и 3. Размещая эти цифры в порядке, мы можем получить различные комбинации.

Комбинация 123: это означает, что цифры расположены в порядке возрастания.
Комбинация 132: здесь первая цифра больше третьей, и они поменялись местами.
Комбинация 213: в этом случае первая цифра меньше второй, но больше третьей.
Комбинация 231: здесь первая цифра меньше третьей, и они поменялись местами.
Комбинация 312: первая цифра больше третьей, но меньше второй.
Комбинация 321: все цифры поменялись местами и находятся в обратном порядке.

Как видим, меняя порядок цифр, мы получаем различные комбинации. Ответ на вопрос «сколько может быть комбинаций из трех цифр» зависит от того, учитывается ли порядок или нет. Если порядок учитывается, то возможностей становится больше, поскольку каждая цифра может занимать любую из трех позиций. То есть, всего может быть 3 * 2 * 1 = 6 комбинаций.

Однако, если порядок не учитывается и цифры просто комбинируются без замены позиций, то всего возможно 3 комбинации: 123, 132 и 213.

Таким образом, порядок имеет влияние на комбинации из трех цифр

Важно учитывать этот факт при решении задач, связанных с комбинаторикой и вероятностями

Простой математический подсчет количества комбинаций

Для понимания, сколько может быть комбинаций из трех цифр, следует применить простой математический подсчет. Для каждой позиции в комбинации у нас может быть любая из 10 цифр (от 0 до 9).

Таким образом, для первой позиции может быть выбрана любая из 10 цифр, для второй позиции также может быть выбрана любая из 10 цифр, и тоже самое касается третьей позиции.

Следовательно, общее количество возможных комбинаций из трех цифр будет равно произведению количества возможных вариантов для каждой позиции, то есть 10 * 10 * 10 = 1000.

Таким образом, сколько может быть комбинаций из трех цифр — 1000.

Комбинации и перестановки:

В английском языке мы используем словосочетание, не задумываясь о важности порядка слов или нет. Просто мой обед состоит из бургера, сэндвича с Рубеном и яблочного пирога

Нас не волнует их порядок, они также могут быть в «сэндвиче с Рубеном, яблочном пироге и бургере», но это та же еда. Также,

Замок сейфа – 584. Теперь, если нас не заботит порядок, то он не работает. Например, 845 не подойдет, а 458 не подойдет. Надо точно ввести 5-8-4. Итак, мы пришли к выводу, что:

Когда порядок не имеет значения, это комбинация, а когда порядок имеет значение, это перестановка. Проще говоря, перестановка – это упорядоченная комбинация.

Исключение чисел с цифрой 6

Для определения количества трехзначных чисел без цифр 5 и 6, необходимо исключить все числа, которые содержат цифру 6.

Чтобы проиллюстрировать это, рассмотрим следующую таблицу:

Первая цифра	Вторая цифра	Третья цифра
1
2
…	…	…
9	9	6

В данной таблице представлены все возможные трехзначные числа, где каждая цифра может принимать значения от 0 до 9.

Однако, поскольку мы хотим исключить числа со значением 6, мы исключим все строки, в которых третья цифра равна 6:

Первая цифра	Вторая цифра	Третья цифра
1
2
…	…	…
9	9	5

Теперь в таблице приведены все возможные трехзначные числа без цифры 6. Всего их 550.

Таким образом, количество трехзначных чисел без цифр 5 и 6 равно 550.

Понятие Комбинаторики и Составление Чисел

Представим, что у нас есть набор из нескольких цифр. Сколько разных чисел можно составить из этих цифр? Чтобы ответить на этот вопрос, обратимся к комбинаторике.

Существует несколько видов комбинаций, которые можно использовать при составлении чисел:

Вид комбинации	Описание
Перестановка	Составление чисел, где порядок цифр имеет значение
Сочетание	Составление чисел, где порядок цифр не имеет значения
Размещение	Составление чисел, где порядок цифр имеет значение, но используются не все цифры

Количество возможных комбинаций зависит от количества цифр в наборе и правил, по которым мы выбираем цифры для составления числа.

Например, если у нас есть набор из трёх цифр: 1, 2 и 3, и мы хотим составить трёхзначное число, то для каждой комбинации имеется 6 различных вариантов:

Таким образом, ответ на вопрос о количестве комбинаций зависит от количества цифр и длины числа, которое мы хотим составить.

Размещения и перестановки в программе Python

Зачем считать, если можно не считать? Для более сложных расчетов нам может понадобиться написать программу, которая будет производить определенные действия с перестановками или размещениями.

Для облегчения работы с ними в Python существует модуль itertools, который содержит инструменты для их создания:

permutations(набор символов) — создает перестановки переданного набора

Все комбинации будут возвращены в виде списка символов.

Пример.

Допустим, мы будем составлять пароли длиной 6 символов из того же набора символов “P”, “A”, “S”, “W”, “O”, “R”, “D”, “1”, “2”, “3”, но с дополненными условиями:

символ “Р” может использоваться в пароле любое количество раз, но обязательно должен быть на первом месте;
символ “3” должен быть использован в пароле ровно 3 раза;
в пароле не должно быть сочетания “123”.

Пошагово наш код должен состоять из следующих элементов:

Для создания всех вариаций пароля будем использовать product модуля itertools, все пароли будем перебирать циклом for. Также предварительно создадим переменную-счетчик подходящих паролей.
Нам нужно проверить все условия задачи. Элемент комбинации с индексом 0 равен “Р”, “3” встречается в ней ровно 3 раза, а также в списке символов комбинации не должно быть набора (“1”, “2”, “3”).
При нахождении подходящего пароля будем увеличивать наш счетчик на 1, в конце программы выведем его значение на экран.

Фактчек

Размещения — наборы последовательностей определенной длины, состоящие из определенных символов, которые могут встречаться в последовательности сколько угодно раз. Количество размещений N зависит от длины последовательности k и количества символов n как N=nk.
Перестановки — наборы последовательностей, отличающиеся только порядком следования символов друг за другом. Количество перестановок N зависит от количества символов в них n как N = n!.
В общем виде количество комбинаций высчитывается как произведение количества возможных символов на каждой позиции.
Для записи перестановок в Python используется permutations из модуля itertools, для записи размещений — product из того же модуля.

Общее количество трехзначных чисел без цифр 5 и 6

Чтобы найти общее количество трехзначных чисел без цифр 5 и 6, мы можем рассмотреть все возможные комбинации трехзначных чисел с цифрами от 0 до 9 и вычесть из этого количества комбинации, содержащие цифры 5 и 6.

Таким образом, общее количество трехзначных чисел без цифр 5 и 6 можно вычислить следующим образом:

Вычисляем количество всех трехзначных чисел, которые можно составить с цифрами от 0 до 9. Это число равно 10 * 10 * 10 = 1000.
Вычисляем количество трехзначных чисел, в которых есть цифра 5. Это число равно 10 * 10 = 100 (в каждой позиции может быть любая цифра, кроме 5).
Вычисляем количество трехзначных чисел, в которых есть цифра 6. Это число также равно 100 (в каждой позиции может быть любая цифра, кроме 6).

Итак, количество трехзначных чисел без цифр 5 и 6 равно общему количеству трехзначных чисел, уменьшенному на количество чисел, содержащих цифры 5 и 6:

Общее количество трехзначных чисел:	1000
Количество чисел с цифрой 5:	100
Количество чисел с цифрой 6:	100
Общее количество трехзначных чисел без цифр 5 и 6:	800

Таким образом, существует 800 трехзначных чисел без цифр 5 и 6.

Краткое описание

Изучение математических правил не может обойти стороной число сочетаний из n по k. Формулы комбинаторики как науки активно используются во всех жизненных отраслях. Этот раздел включён в школьную программу старших классов и вступительные испытания многих вузов России. Удивительная комбинаторика лежит в основе прикладного искусства.

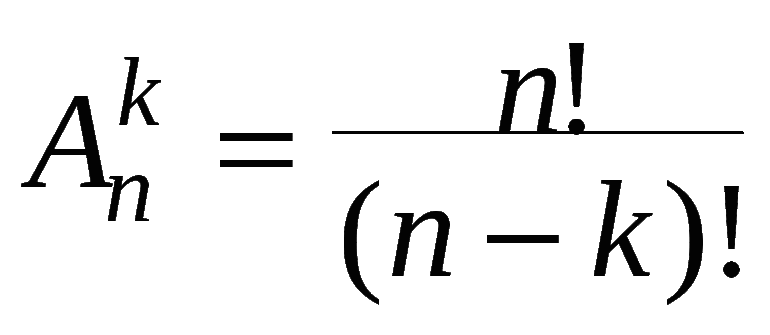
Это направление науки начало активно развиваться ещё шесть веков назад. Достоверно известно, что первые комбинаторные задачи присутствовали в трудах философов и талантливых математиков Средневековья. В те времена представители стремительно развивающегося научного мира всячески пытались найти актуальные методы решения поставленных задач, хотели определить основные правила и понятия, а также утвердить уникальные в своём роде формулы и математические уравнения для тех, кто ещё не знаком с этим научным направлением.

Актуальные формулы и нормы комбинаторики применяются в распространённой теории вероятностей, где специалисты могут быстро и качественно подсчитать процент случайных событий, чтобы в итоге получить закон реального распределения случайных величин