Изменения в проведении ЕГЭ и ОГЭ 2024 от Рособрнадзора
Парламентарий полагает, что подобные выплаты для учащихся вузов должны быть повышены до МРОТ. С начала 2024 г. Еще одной задачей Нилов считает введение в России новых возможностей для учащихся средних специальных учебных заведений. В частности, отметил депутат, им необходимо разрешить начинать свою трудовую деятельность на некоторых предприятиях, где сейчас такие студенты работать не могут.
В пример он приводил идею о внедрении Минпросвещения общих образовательных программ для всех предметов. Больше новостей — в нашем официальном телеграм-канале «Фонтанка SPB online»
Подписывайтесь, чтобы первыми узнавать о важном. По теме
Родители выпускников выбирают — платить репетиторам, чтобы сдать ЕГЭ, или платить за колледж, чтобы его не сдавать… Нужно возвращаться к полностью бесплатной советской системе образования, показавшей себя лучшей в мире, и чем скорее, тем лучше». Не совсем понятно, что имеет в виду Сергей Миронов. Во времена СССР высшее образование и даже старшие классы школы тоже не всегда было бесплатным. Например, постановлением правительства от 26 октября 1940 года «Об установлении платности обучения в старших классах средних школ и в высших учебных заведениях СССР и об изменении порядка назначений стипендий» в СССР была введена общеобязательная плата за обучение для всех учащихся вузов, 8—10-х классов средних школ, а также техникумов, педагогических училищ, сельскохозяйственных и других специальных средних заведений. Отменили это решение только в 1965 году. Продиктована данная мера была государственной необходимостью. В 1940 году почти одновременно с первым вышел другой указ «О государственных трудовых резервах СССР». Уже в первый год после него более 800 тыс. Выпускники этих школ получали направления на предприятия, где обязаны были проработать четыре года. В 1960-е годы образовательный ценз молодежи повысили, ввели обязательное восьмилетнее образование. И отменили плату за обучение в старших классах.
В этом году выпускник должен будет использовать маску подсети при адресации в соответствии с протоколом IP. Физика Больше всего изменений произошло в экзамене по физике. Из первой части удалили задание на распознавание графических зависимостей и два задания на определение соответствия формул и физических величин по механике. Во второй части убрали расчетную задачу высокого уровня сложности. А задание с кратким ответом в виде числа из раздела «МКТ и термодинамика» перенесли в раздел механики. Максимальный балл теперь составляет 45.
Примеры использования

1. Коэффициент оптимизма: В экономике коэффициент оптимизма, тесно связанный с вероятностью, равняется 1/(1+d), где d – это ставка дисконтирования. Чем ниже ставка дисконтирования, тем выше коэффициент оптимизма, это может стимулировать инвестиции и расширение производства.
2. Переменная времени: d также используется в физике и инженерии для обозначения переменной времени. Например, в уравнении движения механической системы x(t) = A*cos(ωt + φ), d может использоваться вместо t: x(d) = A*cos(ωd + φ).
3. Сложные проценты: d в формуле сложных процентов обычно обозначает промежуток времени, в течение которого происходят процентные расчеты. Например, формула FV = PV*(1+r/n)^(nt), где r – годовая ставка процента, n – количество раз, когда происходят расчеты за год, t – количество лет, а d = 1/n – это промежуток времени между расчетами процентов.
4. Скорость роста: d может использоваться для обозначения скорости роста. Например, при моделировании роста населения в формуле N(t) = N0*e^(rt), d может быть обозначен как dt, где t – это время, а r – скорость роста населения.
5. Временные интервалы: d может использоваться для обозначения временного интервала в экспериментальных исследованиях или визуализации данных. Например, в математической модели для анализа временных рядов, где y(t) обозначает значения переменной в каждый момент времени t, d может использоваться для обозначения временного интервала между измерениями.
Это были лишь некоторые примеры использования буквы «d» в математических формулах и уравнениях. Она является неотъемлемой частью многих областей науки и техники, и ее использование может меняться в зависимости от контекста.
Понятие D в различных науках
Буква D имеет различные значения и используется в различных науках. Рассмотрим некоторые из них:
- Физика: В физике буква D может обозначать различные величины или понятия, например: дистанцию (расстояние), децибелы (единицы измерения звукового давления) или дефект (недостаток) в материале.
- Математика: В математике буква D может обозначать различные объекты или операции, например: детерминант (определитель матрицы), диаметр (расстояние между самыми удаленными точками фигуры) или дифференциал (бесконечно малое приращение).
- Химия: В химии буква D может обозначать различные элементы или вещества, например: девергент (вещество, ускоряющее реакцию) или дейтерий (изотоп водорода с атомным номером 2).
- Биология: В биологии буква D может обозначать различные биологические объекты или процессы, например: ДНК (дезоксирибонуклеиновая кислота) или дефицит (недостаток вещества или фактора).
- Информатика: В информатике буква D может обозначать различные технологии или форматы данных, например: база данных (структурированное хранилище информации) или двойное слово (целочисленный тип данных).
Таким образом, буква D играет важную роль в разных областях наук, и ее значение может различаться в зависимости от контекста.
Маленькая D в математике
Маленькая латинская буква D также имеет свое значение в математике. В основном, она используется для обозначения различных математических понятий и обозначений.
Одним из самых распространенных использований маленькой буквы D в математике является ее использование в дифференциальном исчислении. В этом контексте, маленькая D обозначает оператор дифференцирования. Например, если у нас есть функция f(x), то ее производная будет обозначаться как df(x)/dx или просто f'(x), где D или d — это оператор дифференцирования.
Также, маленькая D часто используется в обозначении систем дифференциальных уравнений. В этом контексте, D обозначает дифференциальный оператор. Если у нас есть система уравнений вида:
Dx = 3x — 2y
Dy = 2x + y
то это означает, что мы берем производные по времени от переменных x и y.
Кроме того, маленькая D используется для обозначения некоторых других математических понятий, например, дискретной математики или вероятности. В этих случаях, маленькая D может обозначать дискретную переменную или дискретное распределение.
В общем, маленькая D в математике имеет различное значение в зависимости от контекста, в котором она используется. Она обозначает оператор дифференцирования, дифференциальный оператор или может быть связана с другими математическими понятиями
Важно понимать контекст использования маленькой буквы D, чтобы правильно интерпретировать его значение
Маленькая D в химии
Маленькая «D» в химии также может обозначать сбалансированный дипольный момент молекулы. Дипольный момент характеризует разность заряда в молекуле и его распределение. Маленькая «D» используется для обозначения внутреннего дипольного момента, в отличие от большой «D», которая обозначает полный дипольный момент молекулы.
Маленькая «D» также может означать s- or p-оболочку в химическом контексте. «D» обозначает s-оболочку, которая состоит из сферических электронных орбиталей, в то время как «d» обозначает p-оболочку, которая имеет форму двойной шаровой сферы.
Маленькая «d» также может использоваться в названии соединений для обозначения дека- или декавалентной связи. Например, в органической химии соединение, содержащее два атома углерода, связанных двумя одиночными связями и одной двойной связью, может быть названо «диен».
Маленькая D в биологии
Маленькая буква D часто используется в биологии для обозначения различных понятий и явлений. В данном контексте, D может означать:
| Доминантный | – используется для обозначения доминантных генов или признаков. Доминантные гены проявляются в изменении фенотипа, при этом они маскируют рецессивные гены. |
| ДНК | – в биологии буква D может быть использована для обозначения ДНК (деоксирибонуклеиновая кислота) – основной нуклеиновой кислоты, содержащей генетическую информацию. ДНК состоит из нуклеотидов, которые в своей основе содержат нуклеиновую кислоту и сахарозу. |
| Доза | – D может индицировать количество или дозу чего-либо в биологии. Например, D может быть использована для обозначения дозы вещества в экспериментах или в медицинском контексте. |
| Дезоксирибоза | – D может также использоваться для обозначения дезоксирибозы – пентозного сахара, который является составной частью ДНК и находится в ее молекуле. |
| Дата | – в некоторых контекстах, D может быть использована для обозначения даты в биологических исследованиях или для определения времени проведения экспериментов. |
В Рособрнадзоре рассказали об изменениях в ЕГЭ на 2024 год
Родители выпускников выбирают — платить репетиторам, чтобы сдать ЕГЭ, или платить за колледж, чтобы его не сдавать… Нужно возвращаться к полностью бесплатной советской системе образования, показавшей себя лучшей в мире, и чем скорее, тем лучше». Не совсем понятно, что имеет в виду Сергей Миронов. Во времена СССР высшее образование и даже старшие классы школы тоже не всегда было бесплатным. Например, постановлением правительства от 26 октября 1940 года «Об установлении платности обучения в старших классах средних школ и в высших учебных заведениях СССР и об изменении порядка назначений стипендий» в СССР была введена общеобязательная плата за обучение для всех учащихся вузов, 8—10-х классов средних школ, а также техникумов, педагогических училищ, сельскохозяйственных и других специальных средних заведений. Отменили это решение только в 1965 году. Продиктована данная мера была государственной необходимостью. В 1940 году почти одновременно с первым вышел другой указ «О государственных трудовых резервах СССР».
Уже в первый год после него более 800 тыс. Выпускники этих школ получали направления на предприятия, где обязаны были проработать четыре года. В 1960-е годы образовательный ценз молодежи повысили, ввели обязательное восьмилетнее образование. И отменили плату за обучение в старших классах.
Профильная математика Математику ждут серьезные «реформы». В 2024 г. Ранее за экзамен по «профилю» можно было получить максимум 31 балл. Ещё одним новшеством стало добавление в контрольно-измерительные материалы задания по геометрии с векторами.
В некоторых заданиях требуется вычислить длину вектора, в других — угол между векторами. Литература По аналогии с русским языком и математикой по литературе также уменьшат максимальный первичный балл, теперь набрать получится только 48 баллов вместо 53. Структура экзамена изменится — уменьшится число вопросов с кратким ответом. При написании сочинения от выпускника потребуется выбрать писателя, а не опираться на какое-либо произведение. Информатика Существенных реформ в экзамене по информатике нет. Составители внесли корректировки только в 13 задание. По новым требованиям выпускники должны будут показать способность работать с маской подсети. Ранее в 13 задании спрашивали про графы, требовалось отыскать количество путей на графах.
В новом году работы выпускников будут проверяться быстрее — не более двух дней, ранее эксперты оценивали работы в четырехдневный срок. Физика На удивление выпускников составители ЕГЭ по физике значительно его облегчили. Теперь в экзамене будет 26 заданий вместо прежних 30. Из ЕГЭ по физике исключили задание по графикам, задачи на определение соответствия формул по электродинамике и механике, убрали сложную задачу из второй части.
Структуру задания 18 на установление причинно-следственных связей расписали более подробно, чтобы исключить двусмысленность. Содержание экзамена расширили до событий 2022 года — по истории России и по всеобщей истории. Изменения коснулись только системы оценки задания 24, где нужно составить сложный план. Кроме того, его формулировка стала точнее. Иностранные языки. Задания распределены по базовому и высокому уровням сложности. Задания, где требуется проанализировать данные таблицы и диаграммы, а также описать изображение, стало понятнее — изменились формулировки. Количество баллов за выполнение некоторых заданий стало меньше: 1 аудирование и 11 чтение — 2 балла 2 аудирование и 10 чтение — 3 балла. Максимальный первичный балл снизили до 82 вместо 86.
Отменено понятие «однотипная ошибка»: каждая орфографическая ошибка считается за отдельную. Уточнены критерии К2 и К4: при комментировании необходимо проанализировать смысловую связь между примерами-иллюстрациями, а при обосновании собственного мнения следует включить пример-аргумент, опирающийся на ваш опыт. Уменьшено количество баллов за критерий К2 с пяти до трёх. Критерий К6 стал независимым от критерия К10, за него также уменьшено количество баллов с двух до одного. Уточнена тема сочинения 11. Скорректированы критерии оценивания заданий с развёрнутым ответом. Повышены требования к грамотности. Задания 4. При оценке выполнения заданий 4. Уточнены критерии 6, 7 и 8 при оценивании заданий 11. Из кодификатора убрали все произведения начиная с древнерусской литературы до литературы середины XIX в. Максимальное количество баллов за ЕГЭ по литературе теперь составляет не 53, а 48. Максимальное количество первичных баллов за работу увеличено с 31 до 32.
D как обозначение доллара
Буква D часто используется в качестве обозначения для доллара, особенно в международных финансовых операциях. Данное обозначение имеет историческое происхождение и связано с применением символа $ для обозначения доллара.
Символ $ появился в Америке в XVIII веке, когда различные колонии использовали разные валюты. В то время символы, обозначающие разные валюты, были похожи или имели некоторые схожие элементы. Один из наиболее известных символов — это U с двумя вертикальными линиями, которое использовалось для обозначения испанского песо.
В начале XIX века в США была создана первая банка, которая выпускала бумажные деньги и создала валюту под названием «United States dollar» (доллар США). Для обозначения данной валюты был использован символ S с двумя вертикальными линиями — знак «суперсимиона». Однако, данный символ использовался тогда еще не только для доллара, но и для других валют.
В 1788 году по инициативе Американского конгресса было принято решение о создании нового символа для обозначения доллара. Символом стал S внизу перечеркнутое одной горизонтальной линией — знак «суперсимиона». Таким образом, использовалась аббревиатура «U.S» вместо полного названия «United States».
Однако, символ $, как мы его знаем сейчас, начал широко использоваться с 1800-х годов. Изначально он был использован в газетах и печатных изданиях для обозначения доллара. Позже, он стал широко использоваться в официальной бумажной валюте.
Итак, символ $ стал настолько распространенным, что превратился в главный символ доллара. В связи с этим, буква D стала использоваться в международных финансовых операциях как обозначение для доллара. Например, в обычном выражении 1$ = 1 доллар, в международной записи 1USD = 1 доллар.
Определение дельта-эпсилон
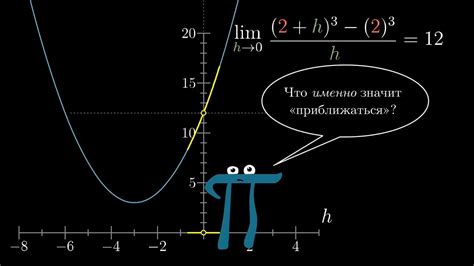
Рассмотрим понятие дельта-эпсилон в контексте математики. Эта концепция используется для аккуратного определения предела функции и установления свойств функций в некоторой окрестности заданной точки. При формальной записи дельта-эпсилон, используются символы «дельта» и «эпсилон», которые обозначают очень малые величины, близкие к нулю, и позволяют строго определить, какое значение функции будет находиться в окрестности заданной точки.
Для определения дельта-эпсилон используется таблица, в которой указываются значения «дельта» и «эпсилон», а также связанные с ними условия и свойства функции. Такая таблица помогает провести точные вычисления и установить ограничения для значений функции в заданной окрестности точки.
Примером использования дельта-эпсилон может служить определение предела функции f(x) при x стремящемся к определенной точке a. Для этого вводятся «дельта» и «эпсилон», такие что для всех x, лежащих в окрестности точки a, должно выполняться условие: если x находится на расстоянии меньшем, чем «дельта» от a, то f(x) будет находиться в пределах «эпсилон» от предела функции f(x) при x стремящемся к a. Таким образом, с помощью дельта-эпсилон можно формально определить и ограничить поведение функции в окрестности заданной точки.
| Символ | Описание |
|---|---|
| Дельта (Δ) | Символ, обозначающий очень малую величину, близкую к нулю |
| Эпсилон (ε) | Символ, обозначающий очень малую величину, близкую к нулю |
| Функция f(x) | Математическая функция, к которой применяется концепция дельта-эпсилон |
| Точка a | Заданная точка, в окрестности которой рассматривается поведение функции |
Примеры дольных единиц
Дольный вектор:
Вектор может быть разделен на дольный вектор, который является его составляющей по определенному направлению. Например, если рассматривать вектор скорости вдоль оси X, то его дольным вектором будет проекция скорости на эту ось.
Дольный угол:
Угол может быть разделен на дольный угол, который является частью полного угла. Например, если полный угол равен 90 градусов, то его дольный угол может быть 45 градусов. Дольные углы используются для измерения поворотов и направлений.
Дольное время:
Время может быть разделено на дольное время, которое представляет собой часть общего времени. Например, если общее время равно 60 секундам, то его дольное время может быть 30 секунд.
Дольная масса:
Масса может быть разделена на дольную массу, которая представляет собой часть общей массы. Например, если общая масса равна 100 граммам, то ее дольная масса может быть 50 граммов.
Дольная площадь:
Площадь может быть разделена на дольную площадь, которая представляет собой часть общей площади. Например, если общая площадь равна 100 квадратным метрам, то ее дольная площадь может быть 50 квадратным метрам.
Дольный объем:
Объем может быть разделен на дольный объем, который представляет собой часть общего объема. Например, если общий объем равен 100 литрам, то его дольный объем может быть 50 литров.
Символ d в математических формулах
Символ «d» широко используется в математических формулах для обозначения дифференциала, который представляет собой малое изменение величины.
Дифференциал обычно применяется, когда необходимо выразить зависимость между функцией и ее аргументом. Символ «d» помогает указать, что переменная является дифференциалом.
Например, если имеется функция «f(x)», где «x» — аргумент функции, то можно записать дифференциал этой функции как «df». Здесь символ «d» обозначает дифференциал, а «f» — функцию.
Дифференциал также может быть записан в других формах, например, «dx» или «dy». В этом случае, «x» и «y» обозначают аргументы функции или переменные, по которым производится дифференцирование.
Обратите внимание, что символ «d» используется не только в дифференциальном исчислении, но и в других областях математики и физики. Например, в интегральном исчислении символ «d» обозначает дифференциал переменной интегрирования
Использование символа «d» в математических формулах позволяет более точно выразить зависимости и взаимосвязи между величинами.
Интерпретация символа d в контексте уравнений
В физике символ d часто используется для обозначения разности величин. Он может иметь различную интерпретацию в разных контекстах. В научных уравнениях символ d может обозначать:
- дифференциал — малое изменение некоторой величины;
- производную — скорость изменения одной величины относительно другой;
- шаг интегрирования — малый интервал, на котором происходит интегрирование;
- инкремент — разность между двумя значениями величины.
Интерпретация символа d зависит от контекста и должна быть установлена в каждом конкретном случае. Он может быть использован в различных областях физики, таких как механика, электродинамика, и термодинамика. В каждой из этих областей символ d будет иметь свою интерпретацию.
Важно понимать, что символ d не является отдельной величиной или операцией. Он всегда используется вместе с другими математическими обозначениями, такими как интегралы или производные
Действительное значение символа d будет определяться контекстом и математическими операциями, сопровождающими его использование.
Использование символа d в физике имеет свою историческую подоплеку, связанную с развитием математики и ее применения в физических науках. Большинство символов и обозначений в физике имеют свое происхождение из математики и стали широко использоваться для обозначения различных физических величин и операций.
В итоге, символ d в контексте уравнений в физике можно рассматривать как знаковое обозначение величин разности или дифференциалов, которое имеет свою специфическую интерпретацию в каждой конкретной ситуации.
Обозначение дифференциала в математических выражениях
Обозначение дифференциала в математических выражениях имеет особое значение и используется для обозначения бесконечно малой приращения величины. Дифференциал представляет собой специальный символ, который обозначается символом «d» перед переменной.
Дифференциал является основным понятием в дифференциальном и интегральном исчислении. Он позволяет описать изменение функции в точке и выразить это изменение в виде отношения двух бесконечно малых величин – приращения функции и приращения ее аргумента.
| Обозначение | Значение |
| d | дифференциал |
| dx | дифференциал аргумента x |
| df | дифференциал функции f |
| dy | дифференциал переменной y |
Дифференциалы позволяют выполнить математические операции над функциями, такие как дифференцирование и интегрирование. Они играют важную роль в физике, где часто используется понятие мгновенной скорости, скорости изменения функции в заданной точке.
В физике символ d также используется для обозначения разности величин. Например, d может обозначать длину пути.
Видео:Урок 3 (осн). Физические величины и единицы их измеренияСкачать

Что такое d в физике
Например, в механике d может обозначать малое приращение или разность между двумя значениями величины. Он может также использоваться как обозначение для малого элемента длины, ширины или высоты.
В электронике и электротехнике, d может обозначать расстояние между двумя точками или элементами. Он может также использоваться для обозначения малого изменения напряжения или тока.
В оптике, d может обозначать малое различие или разность между двумя длинами волн или фазами.
В общем смысле, использование символа d в физике подразумевает, что мы рассматриваем некоторую малую величину, которая может быть важной в контексте рассматриваемого явления или процесса. Примечание: В символике физики также существуют другие символы с префиксом «d», такие как «dx», «dy» или «dz», которые обозначают малые изменения для соответствующих координатных осей
Примечание: В символике физики также существуют другие символы с префиксом «d», такие как «dx», «dy» или «dz», которые обозначают малые изменения для соответствующих координатных осей.
Определение д в физике
Величина децибела рассчитывается с использованием логарифмической шкалы и обычно выражается в десятичных логарифмах. Одно децибел соответствует 1/10 (одной десятой) или приблизительно 0,1 бели.
Значение д в физике является очень важным, поскольку позволяет измерять и выражать различные физические характеристики в удобном логарифмическом масштабе. Например, децибелы позволяют измерять громкость звука, сравнивать уровень мощности или уровень сигнала в электронных системах, а также оценивать основные физические параметры в различных областях науки и инженерии.
В физике д играет важную роль при измерении и анализе сигналов и шумов, электрических и звуковых колебаний, акустических и радиоволн, а также во многих других областях научных исследований.
Поэтому понимание значения д и его использование в физике является необходимым для всех, кто работает в области измерения и анализа различных физических величин.
Перевод д в системах измерения
Перевод декад в системах измерения может быть осуществлен при помощи таблицы:
| Единица измерения | Значение |
|---|---|
| Декада | 10 |
| Секунда | 0.1 |
| Минута | 0.00167 |
| Час | 2.78 x 10^-5 |
| Сутки | 1.16 x 10^-6 |
| Неделя | 1.65 x 10^-7 |
| Месяц | 3.81 x 10^-8 |
| Год | 3.17 x 10^-9 |
Таким образом, декада представляет собой значительную величину в сравнении с единицами времени, такими как секунда или минута. Она широко используется для измерения больших промежутков времени, например, в геологии или астрономии.
Примеры использования д в физике
Константа д, также известная как дебайевский коэффициент, широко используется в физике для описания различных физических явлений. Ниже приведены несколько примеров использования д в различных областях физики:
- В термодинамике: д используется для определения коэффициента объемного расширения материала. Он определяет, насколько изменится объем материала при изменении его температуры.
- В оптике: д используется для определения показателя преломления материала. Он описывает, как свет будет преломляться при переходе из одной среды в другую.
- В акустике: д используется для определения скорости звука в среде. Обычно он связан с плотностью и модулем упругости среды.
- В электромагнетизме: д используется для определения диэлектрической проницаемости материала. Он описывает, насколько электрическое поле может проникать в среду.
- В механике: д используется для определения коэффициента демпфирования системы. Он описывает, насколько быстро система теряет энергию под воздействием силы трения или сопротивления.
Это только несколько примеров использования д в физике. Константа д играет важную роль в описании и понимании различных физических явлений и процессов.
Важность понимания кратных и дольных единиц
Понимание кратных и дольных единиц является важной основой для изучения физики и других естественных наук. Кратные и дольные единицы позволяют нам измерять различные физические величины в удобных и понятных единицах
Кратные и дольные единицы используются для измерения различных физических величин, таких как масса, длина, время, сила и т.д. Например, чтобы измерить массу объекта, мы можем использовать граммы или килограммы. Кратные единицы, такие как килограммы, используются, когда нужно измерить большие значения массы, а дольные единицы, такие как граммы, используются, когда нужно измерить маленькие значения массы.
Понимание и использование кратных и дольных единиц также помогает нам сравнивать и оценивать различные физические величины. Например, используя килограммы, мы можем сравнить массу двух объектов и определить, который из них тяжелее. Также, зная, что в 1 килограмме содержится 1000 граммов, мы можем легко конвертировать массу из одной единицы в другую.
Кратные и дольные единицы также играют важную роль в научных расчетах и формулах. Например, в законе Ньютона о силе, сила измеряется в ньютонах, которые являются кратной единицей, а масса измеряется в килограммах, которые являются дольной единицей. Используя правильные кратные и дольные единицы, мы можем проводить точные и согласованные расчеты и получать правильные результаты.
В заключение, понимание кратных и дольных единиц является необходимым для правильных измерений, сравнений и расчетов в физике. Они помогают нам измерять и оценивать различные физические величины и проводить точные расчеты
Поэтому важно усвоить и применять эти понятия при изучении физики и других наук
Определение термина «диполь» и его значение в физике
В физике диполем также называют систему, состоящую из электронного облака и ядра атома, при условии, что электронное облако имеет такую форму и распределение зарядов, которые можно считать эквивалентными точечным зарядам.
Диполи являются объектами особого интереса в физике из-за того, что они создают электрическое поле, которое изменяется с расстоянием. Также диполи обладают моментом диполя, который является мерой силы действия диполя в электрическом поле.
Значение диполя в физике состоит в том, что он позволяет объяснить и предсказать электрические свойства различных веществ и материалов. Дипольное взаимодействие играет важную роль в таких процессах, как поляризация вещества, возникновение диэлектрической проницаемости, поглощение и рассеяние света, а также взаимодействие молекул в химических реакциях.
| Свойства диполя | Примеры применения |
|---|---|
| Момент диполя | Описание поляризации вещества в электрическом поле |
| Электрическое поле диполя | Рассеяние и поглощение света в оптике |
| Дипольный момент атома | Взаимодействие молекул в химических реакциях |
Итак, диполь — это важное понятие в физике, которое широко применяется для анализа и понимания различных явлений, связанных с электричеством и оптикой. Понимание основных свойств и применения диполя помогает развивать науку и технологии в различных областях




























