Решение математических задач в maple

Введение

Maple является одним из самых мощных математических пакетов. Возможности этой программной среды способны охватить очень большое количество разделов математики и могут с пользой использоваться на различных уровнях, в том числе и уровень серьезных научных исследований.

Работать с Maple возможно как в режиме интерактивного диалога, так и путем формирования и отладки программ на специализированном Maple-языке, который ориентирован на усложнённые математические вычисления. Основой пакета считается специальное ядро, то есть, программа символьных преобразований. Помимо этого, присутствует набор из нескольких тысяч специальных функций, которые хранятся в подгружаемых к ядру пакетах и библиотеках. Общая ориентация пакета на символьные преобразования, то есть, компьютерную алгебру, вовсе не означает, что при помощи Maple невозможно решать задачи численными методами.

Статья: Работа в среде Maple

Найди решение своей задачи среди 1 000 000 ответов

Maple способна не только осуществлять вычисления, но также имеет и богатые возможности графического отображения математических объектов и процессов.

Примеры

Нет ничего практичней хорошей теории и нет ничего численней хорошего аналитического
решения задачи. Пример на рис. 5 особо поражает тех, кто занимается или
когда-то занимался составлением программ решения дифференциальных уравнений. В
среде Maple эта задача решается буквально в два счета: запись уравнения (делай
раз — см. рис. 5) и его решение в аналитическом виде (делай два).

Рис. 5. (на отдельном листе)

Возвращаясь к теме интерфейса Maple и анализируя рис. 5 и другие
иллюстрации, отметим, что документ Maple может быть пользователем структурирован:
если щелкнуть по кнопке, расположенной левее названия параграфа, то
соответствующая область захлопнется и останется только название параграфа и
кнопка, но уже с плюсом, а не с минусом внутри. Это очень удобно при работе с
объемными документами. Такая технология заложена во многие Windows-приложения —
в текстовый редактор Word, например. В последних версиях Maple (Release 4) и
Mathcad (6.0) допустимы гипертекстовые ссылки, которыми, кстати, изобилует и
эта статья (см. рис., см. выше, см. ниже и т.д.).

Инструменты символьной математики Mathcad (рис. 6) позволяют найти одно
из решений дифференциального уравнения, записанного на рис. 5. Но пользователю
при этом придется поработать головой и руками, преобразуя исходное уравнение в
интегральное, копируя промежуточные выкладки и т.д. Знание математики нелишне и
при работе с Mathcad.

Решение дифференциального
уравнения

Исходное уравнение

Разделение переменных и преобразование в
интегральное (ручная работа)

Решение относительно x (команда из меню Symbolic)

Упрощение

Формирование одного из решений (ручная работа)

Поверка

Рис. 6

Как понимает читатель (вернее, знает из курса высшей математики) не всякое
дифференциальное уравнение имеет аналитическое решение, да и не всякое
существующее аналитическое решение удается найти. Кроме того, очень часто
аналитическое решение бывает настолько громоздким, что от него приходится
отказываться, если, тем более, нужно найти решение в точке. На рис. 8 и 9
решается известная задача о развитии эпидемии. Ее уникальность в том, что она
единственная, авторство которой (John Truxal) отмечено в разделе
Acknowledgments документации пакета Mathcad. Суть задачи. В городе с 22 000
жителей появляются 50 инфекционных больных, что вызывает эпидемию. Предположим,
что прирост больных за день пропорционален (с коэффициентом Pr)
произведению числа здоровых (еще не переболевших и не приобретших иммунитет) на
число больных. Спрашивается, как развивается эпидемия — как изо дня в день
(переменная t) меняется число больных (функция x) и число
здоровых (y). Проблема сводится к решению задачи Коши для системы двух
обыкновенных дифференциальных уравнений.

Рис. 7 (на отдельном листе)

Maple отказался решить систему аналитически или через преобразования Лапласа
(method=laplace). Однако с удовольствием и легко решил ее приближенно с
использованием степенных рядов (type=series) и численно (type=numeric).
Забегая вперед, отметим, что в среде Maple есть специальный тип графиков, для
отображения решения дифференциальных уравнений (odeplot). В п. 4 на рис.
8 синяя кривая отмечает изменение во времени числа здоровых, черная — больных,
а красная — здоровых, подсчитанная через степенной ряд.

Задача об эпидемии в среде Mathcad

Исходные данные

Два дифференциальных уравнения

Численное решение

График решения

Рис. 8

На рис. 9 представлен протокол решения в среде Maple задачи о равновесии
балки (поиск реакции опор X, Y и Р), сводящееся к решению
системы из трех алгебраических уравнений, описывающих баланс сил и моментов
сил. Задача решается полностью на аналитическом уровне и заканчивается
формированием функции Y, по которой строится трехмерный график.

Рис. 9 (на отдельном листе)

«По одежке встречают, по уму провожают»

01.03. Работа С Переменными

* Clearing Variables *

Достаточно Вам однажды определить
переменную, — и Maple будет помнить её значение на
протяжении всей Вашей рабочей сессии на
компьютере. Если Вам понадобилось
переопределить переменную — просто выполните
новую операцию присваивания.

Например, в каждой из приведенных ниже
строк в преобразованиях участвует переменная h
.( Замечание : для слежения за текущим
значением переменной h не забывайте
заканчивать ввод символом » точка с запятой
«, а не » двоеточие «.)

> h;

> h:=56;

> h;

> h:=sqrt(Pi);

> h;

Иногда возникает желание
«очистить» переменную в памяти для того,
чтобы её имя впоследствии использовать в иных
целях.

Например, присвоим переменной х значение
65 :

> x:=65;

Теперь предположим, что мы, начиная
решение другой задачи, желаем присвоить имя w
квадратному трёхчлену . Если без проволочек
выполнить указанную операцию присваивания, Maple
не задумываясь вместо переменной х подставит её
численное значение:

> w:=x^2-4*x+7;

Чтобы переменная w предстала именно
в алгебраической форме, мы должны «очистить»
аргумент х от присвоенного ранее значения. На
практике это означает подчистку внутренней
памяти Maple. Это можно осуществить посредством
операции x:=’x’; . ( Не путайте только одинарные
и двойные кавычки! )

Чтобы увидеть, как это работает,
выполните приведенные ниже командные строки:

> x:=’x’;

> w:=x^2-4*x+7;

* Одновременная очистка всех переменных:
команда restart *

Команда restart полностью очищает
внутреннюю память Maple от всех определений,
которые Вы совершили в процессе работы.
Фактически, применение команды restart
открывает новую Maple-сессию. Если Вы приступаете к
решению совершенно новой задачи, советуем
использовать restart для полной гарантии того,
что предыдущие преобразования и вычисления не
повлияют на её решение.

Выполнив первую из предложенных ниже
командных линий, постарайтесь предсказать
результат выполнения второй строки:

> p:=4;

> p; x; h;

Конечно, Вы видете, что переменной р
присвоено значение » 4 «, а переменная х
была очищена от своего предыдущего числового
значения. Но очень вероятно, что Вы уже подзабыли,
что переменной h было присвоено значение

Вот
почему так соблазнительна идея частого
использования команды restart , чтобы в одно
мгновение очистить память Maple от «грязи»
.(Если Вы будете внимательно прорабатывать
материал нашей обучающей программы, то обратите
внимание: большинство разделов начинается
именно командой restart )

> restart;

> p; x; h;

Решение дифференциальных уравнений

Решение дифференциальных уравнений и систем дифференциальных уравнений — важный и большой раздел математики. Maple всегда лидировала в средствах такого решения и его визуализации. Аналитические и численные методы решения дифференциальных уравнений годами оттачивались в многочисленных предшествующих версиях Maple, и весь этот мощный аппарат, естественно, вошел в новую реализацию Maple 17. Более того, фирма Maplesoft объявила, что в Maple 17 включено множество новых алгоритмов, команд, функций и опций для аналитического и численного решения систем дифференциальных уравнений, в том числе некоторых новых классов.

Для решения обыкновенных дифференциальных уравнений служит функция dsolve с большим набором опций. Приведем пример ее применения для аналитического решения одного дифференциального уравнения:

> dsolve(diff(y(x),x)–a*x=0,y(x));
> dsolve(diff(y(x),x)–y(x)=exp(–x),y(x));
> infolevel := 3:
> dsolve(diff(y(x),x)–y(x)=sin(x)*x,y(x));
Methods for first order ODEs:
--- Trying classification methods ---
trying a quadrature
trying 1st order linear
<- 1st order linear successful

В этом примере команда infosolve устанавливает уровень вывода решения.

Приведем примеры аналитического решения систем из двух дифференциальных уравнений (в том числе с заданием начальных условий):

> sys := diff(y(x),x)=2*z(x)–y(x)–x, diff(z(x),x)=y(x);fcns := {y(x), z(x)};
dsolve({sys,y(0)=0,z(0)=1},fcns);

> Order:=8:dsolve({sys,y(0)=0,z(0)=1},fcns,series);

> dsolve({sys,y(0)=0,z(0)=1},fcns,laplace);

В двух последних примерах решение представлено в виде степенного ряда, причем в последнем случае использовано преобразование Лапласа.

На рис. 18 показан пример решения дифференциального уравнения с построением асимптотических решений на фоне графика векторного поля. Векторное поле строится короткими стрелками, которые указывают на направление изменения поля. Подобное решение относится к сфере профессиональных методов решения дифференциальных уравнений. Для этого используется пакет расширения DEtools (и PDEtools для решения дифференциальных уравнений в частных производных).

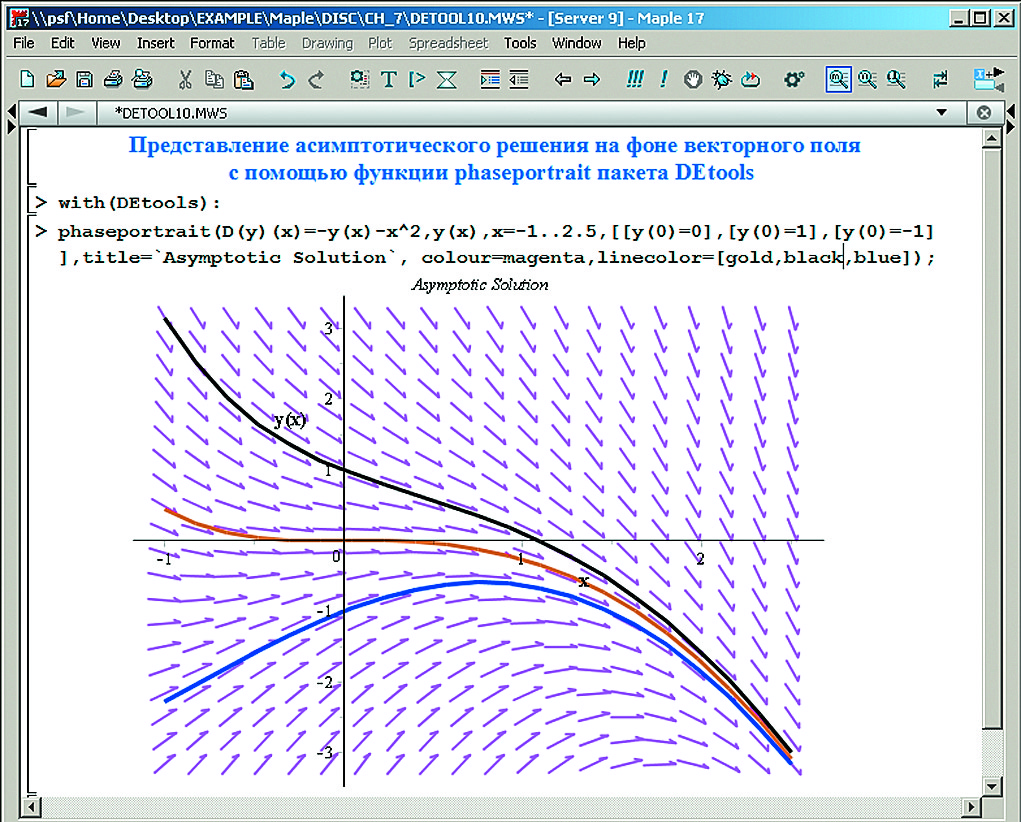
Рис. 18. Пример асимптотического решения дифференциального уравнения

Операции компьютерной алгебры и математического анализа

Операции компьютерной алгебры хорошо известны пользователям Maple и подробно описаны в книгах . В Maple 17 они сохранены и расширены. Поэтому ограничимся несколькими примерами с применением функции упрощения simplify:

> restart;
> simplify(sin(x)^2+cos(x)^2,trig);
> e:=cos(x)^5+sin(x)^4+2*cos(x)^2–2*sin(x)^2–cos(2*x);

> simplify(e);

> simplify(GAMMA(n+4)/GAMMA(n),GAMMA);

> r:=RootOf(x^2–2=0,x):

> simplify(r^2,RootOf);

> simplify(1/r,RootOf);

> simplify(ln(x*y),power,symbolic);

При анализе сигналов часто используются функции интегральных преобразований, например Гильберта, Лапласа и Фурье. Maple обеспечивает получение таких функций для аналитических и численных расчетов . В систему включено огромное число функций. Advisor функций обеспечивает легкое получение их свойств:

> FunctionAdvisor( definition, exp);

> FunctionAdvisor(definition, GAMMA(z));

> FunctionAdvisor(analytic_extension, GAMMA);

Многие функции имеют двойное назначение. Если их имя начинается с большой буквы, функции называют инертными — они выводят аргумент в обычной математической форме, но блокируют выдачу результатов вычислений. Обычные функции с именами, начинающимися с малой буквы, выдают результат вычислений. В строках ввода функции и команды могут записываться в текстовой или математической форме (например, с помощью палитр математических символов).

Примеры вычисления сумм, произведений, производной и интегралов:

> restart; sum(i/(i+1),i=0..n);

> restart; sum(–exp(–k),k);

> sum(k*a^k,k);

> sum(1/k!,k=0..infinity);

> restart; Product(k^2,k=1..5)=product(k^2,k=1..5);

> Product(k^2,k)=product(k^2,k);

> restart; Diff(sin(x)^2,x)=diff(sin(x)^2,x);

> restart; Int(1/sqrt(1–x^2),x=0..1)=int(1/sqrt(1–x^2),x=0..1);

> Int(exp(–t)/t^(1/3), t=0..infinity)=int(exp(–t)/t^(1/3), t=0..infinity);

> Int(Int(Int((x^2+y^2)*z,x=0..a),y=0..a),z=0..a);

Для пошагового вычисления интегралов имеется маплет с графическим интерфейсом пользователя (GUI) (рис. 8). Подобные маплеты в Maple 17 есть практически по всем основным средствам компьютерной алгебры и математического анализа. Имеется также возможность создавать маплеты самим пользователем.

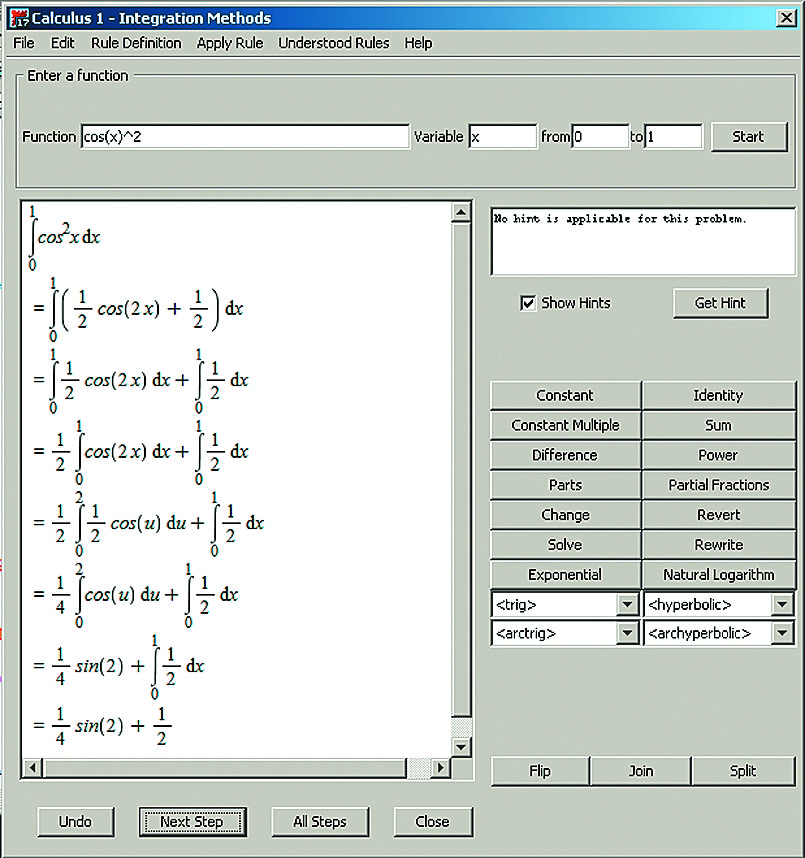
Рис. 8. Маплет для реализации пошагового интегрирования разными методами

Вычисление фундаментальных пределов иллюстрируют примеры:

> Limit(sin(x)/x,x=0)=limit(sin(x)/x,x=0);

> Limit((1+x)^(1/x),x=0)=limit((1+x)^(1/x),x=0);

> Limit((1+1/x)^x,x=infinity)=limit((1+1/x)^x,x=infinity);

> Limit(ln(1+x)/x,x=0)=limit(ln(1+x)/x,x=0);

> Limit((exp(x)–1)/x,x=0)=limit((exp(x)–1)/x,x=0);

> Limit(((1+x)^a–1)/x,x=0)=limit(((1+x)^a–1)/x,x=0);

Следующие примеры показывают решение уравнений и системы из двух уравнений:

> fsolve(x^5–x,x,complex);

> solve(erf(x)=1/2,x);

> fsolve(erf(x)=1/2);

> restart;eq:=exp(–x)=x;sol:=fsolve(exp(–x)=x,x);

> restart;eq1:=a*x+b*y=e; eq2:=c*x+d*y=f;

> solve({eq1,eq2},{x,y});

Работа в среде Maple

Окно Maple включает в свой состав многие атрибуты, которые являются понятными пользователям других приложений Windows, а именно:

1. Заголовочная часть.
2. Строку ниспадающих меню.
3. Панель управления.
4. Линейка вертикальной прокрутки.
5. Строка состояния и так далее.

В главной части основного окна расположено еще одно окно, в котором обычно помещаются один или несколько рабочих документов (Maple worksheet). В этом же окне могут находиться также окна помощи. Состояние ниспадающих и контекстного меню и клавиш на панели управления определяются тем обстоятельством, какое именно окно является активным на текущий момент и месторасположением курсора в окне Maple worksheet.

Рассмотрим самый типичный случай, а именно, работу пользователя над рабочим документом в режиме непосредственного диалога с программой. В данном случае на рабочем документе может представляться текстовая информация трех типов, а также объекты двумерной и трехмерной графики.

Выполняемые команды должны вводиться после специального приглашения «>», красным цветом и обязаны оканчиваться точкой с запятой или двоеточием. Как правило, команды заносятся в строчном формате, но у пользователя также есть возможность перехода к специальному математическому формату, который по умолчанию используется при выводе. В одной строчке могут располагаться несколько команд. Когда после команды стоит двоеточие, то итоговый результат ее исполнения не отображается на дисплее. Когда же после команды поставлена точка с запятой, то после её исполнения на мониторе отобразится результат. Если Maple не смогла выполнить вычисление введенного выражения, то результатом станет перевод заданного выражения в математический формат, который принят для вывода. Выходные данные отображаются по умолчанию синим цветом. Выполнение Maple-команды может быть инициировано нажатием клавиши ввод.

Команды могут объединяться в исполняемые группы. Все такие группы выделяются слева общей для всех содержащихся в ней строк квадратной скобкой. Группа может быть запущена на выполнение одним нажатием клавиши Enter и считается, по сути, самой простой Maple-программой. Для того чтобы не выполнять каждую строку отдельно, а выбрать целую исполняемую группу, достаточно выполнить перевод строки при помощи комбинации клавиш Shift+Enter.

Объединить исполняемые группы возможно путём нажатия функциональной клавиши F4, а разбить группы можно нажатием клавиши F3. Естественно, что все эти операции можно исполнить путём выбора соответствующих пунктов в верхнем меню.

Текст, написанный черным цветом, применяется для комментариев, и он не подлежит обработке системой. Для ввода такого текста, достаточно, находясь в командной строке, нажать клавишу «Т» на панели управления, или выполнить вставку параграфа, путём выбора соответствующего пункта раздела «Insert» в ниспадающем меню.

Рабочий документ Maple может быть структурирован путём создания вложенных друг в друга секций. Эти секции могут быть свёрнуты. В свернутом формате все секции представлены только своими заголовками и признаками секций, а именно, кнопкой, которая снабжена знаком «+». Чтобы развернуть или свернуть секции достаточно нажать на данную кнопку указателем мышки.

При помощи пункта меню «HyperLink…» из подраздела «Insert» имеется возможность создания ссылок на необходимые разделы других рабочих документов и требуемую помощь. Это означает, что Maple-документ способен обладать структурой гипертекста.

Задачи, которые решаются в линейной алгебре, считаются самыми распространёнными в научной и технической областях, а также в образовательной сфере. Решение подобных задач может быть реализовано также при помощи программного приложения Maple.

Ещё одним достоинством системы компьютерной алгебры Maple считается возможность реализации процедур аналитики в символьном формате над матрицами и векторами. Прежде чем осуществить исполнение символьной операции с векторами и матрицами следует сделать очистку памяти от предыдущих определений с помощью команды restart. Когда отдельные элементы вектора или матрицы были определены ранее, то это может привести к значительным изменениям вида итоговых результатов. Но если выполнена предварительная очистка памяти, то вероятность такой ошибки полностью исключена.

Основным достоинством системы компьютерной алгебры Maple считается способность решать задачи линейной алгебры с использованием символьного формата. Но необходимо отметить, что решение в таком формате применяется больше в теории, чем при решении практических задач.

Программирование

Средства реализации сложных алгоритмов были введены только в самую последнюю
и полную версию Mathcad PLUS 6.0 . Maple же с самого начала задумывался как язык
управления символьными преобразованиями. Команды, приведенные в рисунках
статьи, как уже было отмечено ранее, выполняются немедленно после
нажатия клавиши Enter. Но ничто не мешает собрать эти команды и сформировать из
них новые функции и процедуры, поместить их в тело цикла, в тело — альтернативы
и т.д.

Язык Maple, как сказано в его описании , fortran-подобный. Имеется ввиду,
что он не prolog-подобный и не lisp-подобный. Он, скорее всего, BASIC-подобный.
И не только из-за возможности непосредственного выполнения операторов, но и
из-за своего синтаксиса. Отличия в деталях. Разработчики языка Maple,
по-видимому, увлекаются палиндромами — см. знаменитую строчку А.Фета в
эпиграфе подзаголовка, читающуюся одинаково и слева направо и справа налево. На
языке Maple начало альтернативы как и во всех других языках начинается ключевым
словом IF, а конец- новым ключевым словом FI (IF
наоборот).Такая же заготовка-палиндромам(DO…OD)
предусмотрена для тела цикла и т.д. Программисту наконец-то открывается широкая
возможность написания программ-палиндромовтипа IF A THEN
NEHT A FI. Написание стихов-палиндромов относится к области
экспериментальной поэзии (В.Хлебников и др.). Язык Maple может быть
инструментом экспериментального программирования.

Язык Maple обладает всеми качествами ”настоящего” языка программирования.
Все знают, что написать программу можно за 5 минут, а на нахождение ошибки в
ней может уйти целая неделя. Язык Maple оборудован средствами отладки.

Maple состоит из ядра (kernel), написанного на языке С и включающего
поддержку основных функций. Из ядра пакета можно вызывать большое количество библиотек
(см. команду with(название библиотеки) в рисунках статьи), написанных на
языке Maple. В Release 4 насчитывается 31 библиотека: combinat, combstruct, DEtools,
difforms, Domains, finance, GaussInt, genfunc, geometry, grobner, group,
inttrans, liesymm, linalg, logic, LREtools, networks, numapprox, numtheory,
orthopoly, padic, plots, plottools, powseries, process, simplex, stats,
student, sumtools, tensor и totorder. Такой полный набор инструментов
определяет и высокую цену пакета, которая в свою очередь требует защиты — Maple
V Release 4 работает только с электронным ключом. Размещение всех библиотек
требует до 24 Мб дискового пространства.

В этом, честно говоря, одна из главных причин низкой популярности у нас
пакета Maple по сравнению с Mathcad. Приобретая Maple, пользователь покупает
своеобразный “подарочный набор”, включающий вещи. которые ему может быть
никогда не понадобятся. Кроме того, универсальность очень часто (увы!)
подразумевает облегченность — нельзя объять необъятное. Автор, к примеру,
протестировал библиотеку simplex (решение задач линейного
программирования симплекс-методом). С учебными задачами она справляется, но
если их слегка усложнить, то ответа можно и не дождаться. Maple явно
перегружен. Из-за этого, например, многие одноименные встроенные функции имеют
разное содержание и разные аргументы после загрузки разных пакетов.
Разработчики Mathcad “пошли иным путем”. Они сделали ставку на электронные
учебники и на Internet. Нужно пользователю решить дифференциальное уравнение —
он либо покупает за отдельные деньги соответствующий учебник, содержащий и
описание задачи и функции, ее решающие, либо через Internet открывает файл с
прототипом задачи на отдаленном сервере. Одновременно с Maple V Release 4 (лето
1996) на рынке появилась новая версия Mathcad под названием StudyWorks. Она
стоит что-то около 50 $US, содержит мультимедийный обучающий курс и, а это
главное, предоставляет пользователям широкие возможности коллективной работы
через сеть Internet. Плата за использование чужих открытых библиотек — это
разработка и открытие миру своих собственных.

Автор выражает глубокую признательность И.П.Боровикову — генеральному
директору фирмы SoftLine и K.M.Heal — менеджеру фирмы Waterloo Maple за
возможность работы с лицензионными копиями Mathcad и Maple.

Литература:

1. Сказ про то, как Mathcad
   задачу решал. КомпьютерПресс. 1-2’95

1. Блеск и нищета символьной
   математики. КомпьютерПресс. 6’95

1. Язык программирования
   Mathcad. КомпьютерПресс. 6’96

1. K.M.Heal, M.L. Hansen, K.M.
   Rickard. Maple V.
   Learning Guide. Springer Verlag, 1996

1. M.B.Monagan, K.O.Geddes, K.M.Heal,
   G.Labahn, S.M.Vorkoetter. Maple V. Programming Guide. Springer
   Verlag, 1996

Прорыв в скорости вычислений

В последние два-три года пользователи наблюдали огромные успехи команды фирмы Wolfram Research Inc. в совершенствовании системы компьютерной алгебры Mathematica. Вышли на рынок версии Mathematica 6, 7, 8 и 9. Каждая их них добавляла в ядро системы сотни новых команд и функций, а их время вычислений уменьшалось в десятки раз за счет улучшения алгоритмов и применения параллельных вычислений, возможных в современных ПК с многоядерными микропроцессорами.

Фирма Maplesoft — разработчик Maple развила «гонку версий» системы Maple с явным акцентом на совершенствование интерфейса пользователя и с меньшими успехами в обеспечении высокой производительности . Многим уже казалось, будто Mathematica обошла Maple и стала бесспорным лидером среди систем компьютерной алгебры. Однако за последний год положение явно изменилось в пользу Maple в связи с разработкой и выходом на рынок последних версий Maple 16 и 17.

Версия Maple 17 совершила прорыв в области ускорения вычислений даже в сравнении с предшествующей версией Maple 16. При этом в сотни раз уменьшено время вычисления элементарных математических функций, имеющих довольно сложные алгоритмы вычислений (рис. 4а).

Рис. 4. Сравнение Maple 16 и Maple 17 по времени:
а) вычисления элементарных функций;
б) выполнения операций линейной алгебры при работе в операционной системе MAC OS;
в) выполнения операций вычисления собственных значений в операционной системе Windows 7

На рис. 4б показано сравнение Maple 16 и Maple 17 по времени выполнения операций линейной алгебры при работе в операционной системе MAC OS корпорации Apple. Здесь при больших размерах массивов разница не столь сенсационная, но, как правило, составляет не меньше десятка раз. Скорость вычисления собственных значений больших матриц иллюстрирует рис. 4в (64‑разрядная операционная система Windows 7).

Особенно поражает малое время вычислений при символьных (аналитических) вычислениях компьютерной алгебры. Чтобы избежать недоверия пользователя, разработчики Maple 17 пошли на беспрецедентный шаг — поместили в справку конкретные данные о времени выполнения различных аналитических вычислений в сравнении Maple 17 с предшествующей реализацией Maple 16 и даже новейшей Mathematica 9, выпущенной также в 2013 году. Применяемые для этого тестовые примеры даны на рис. 5.

Рис. 5. Шесть тестовых аналитических примеров (проблем)

На рис. 6а сравниваются системы Mathe-matica 9, Maple 16 и Maple 17 по скорости выполнения операции умножения для различных тестовых примеров. Для операции деления сложных выражений результаты приведены на рис. 6б. Выполнение функции factor над полученными ранее выражениями показано на рис. 6в.

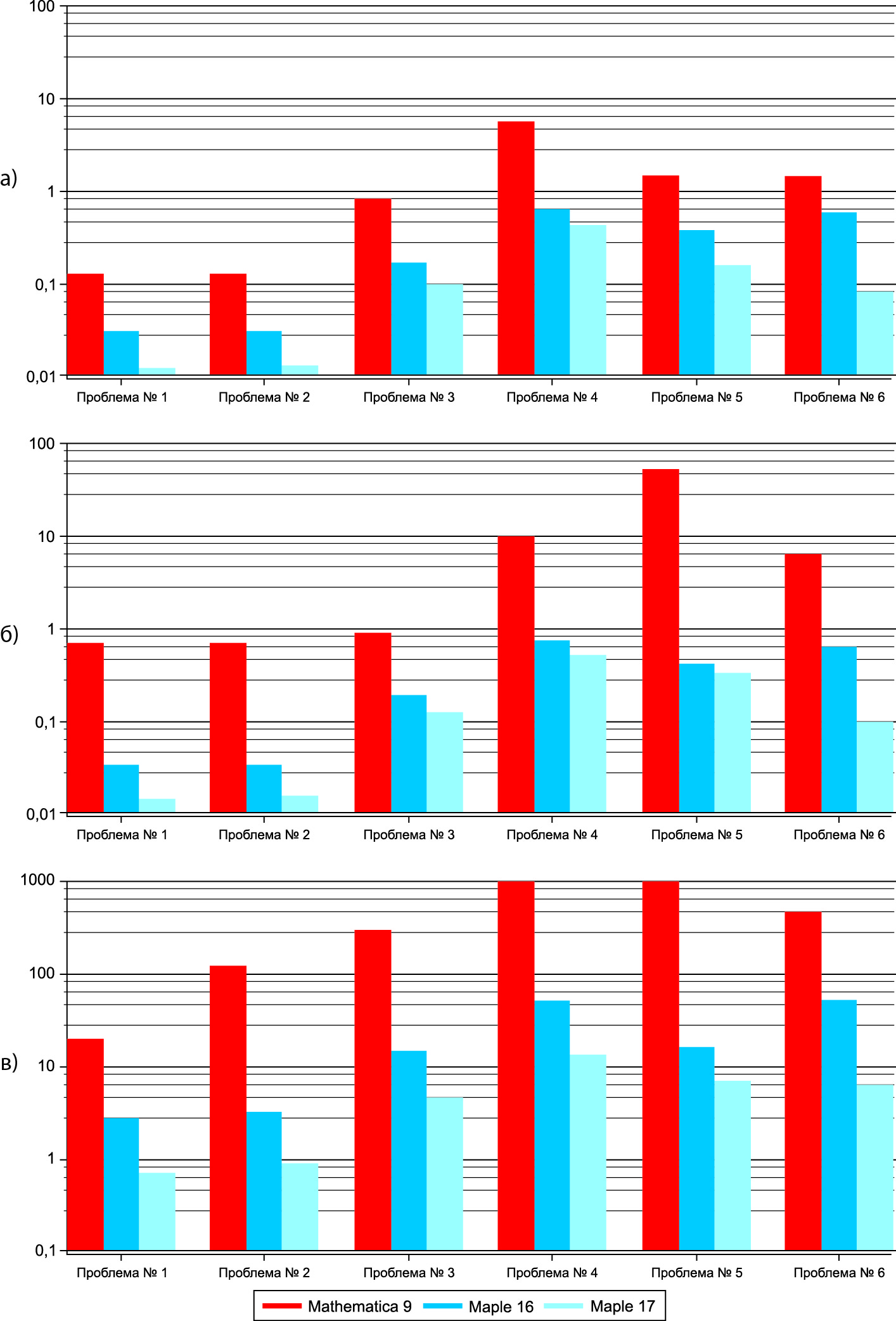
Рис. 6. Сравнение Mathematica 9, Maple 16 и Maple 17 по скорости выполнения операции для различных тестовых примеров:
а) умножения;
б) деления;
в) функции factor

Факторизация более простых выражений показывает резкое уменьшение времени вычислений в системе Maple 17 (рис. 7а). Время выполнения операции расширения сложных выражений иллюстрирует рис. 7б. И здесь время вычислений в Maple 17 заметно меньше, чем у других систем.

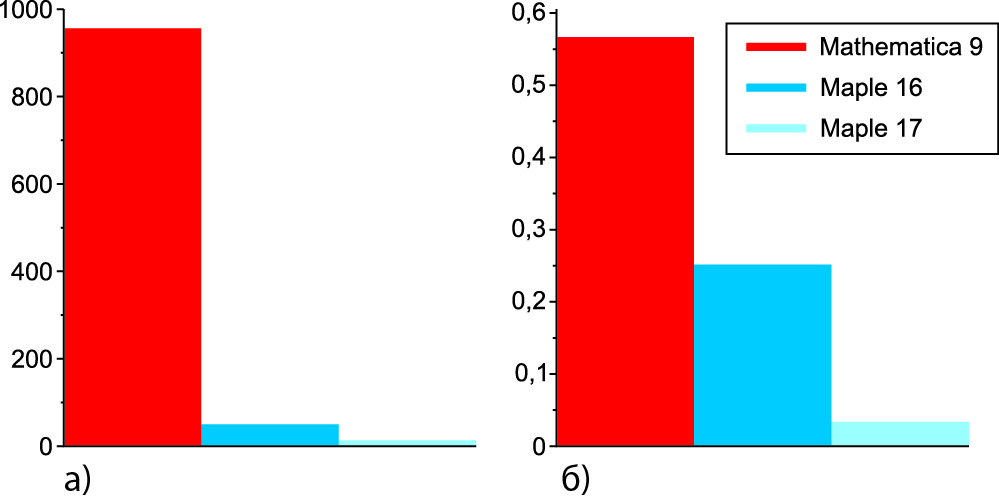
Рис. 7. Время выполнения операции:
а) факторизации;
б) расширения Expand

Функции в Maple. Операции оценивания. Решение уравнений и неравенств

Контрольные задания

1. Дано комплексное число

> restart;

> z:=(2*exp(I*Pi/6))^5:

> evalc(Re(z)); evalc(Im(z));

> evalc(readlib(polar)): evalc(polar(z));

2. Записать функцию

xy

> restart;

> f:=(x,y)->(arctan(x+y)/arctan(x-y))^2;

> f(1,0);

> f((1+sqrt(3))/2,(1-sqrt(3))/2);

3. Записать функцию

xayasubs

> restart;

4. Найти все точные решения системы

> restart;

5. Найти все решения тригонометрического уравнения

> restart;

> _EnvAllSolutions:=true:

> solve(sin(x)^4-cos(x)^4=1/2, x);

6. Найти численное решение уравнения

> restart;

> x:=fsolve(exp(x)=2*(1-x)^2, x);

7. Решить неравенство

> restart;

> s:=solve(2*ln(x)^2-ln(x) f:=sin(x)+cos(x);

Если задать конкретное значение переменной х, то получится значение функции f для этого х. Например, если продолжить предыдущий пример и вычислить значение f при

После выполнения этих команд переменная х имеет заданное значение

Чтобы насовсем не присваивать переменной конкретного значения, удобнее использовать команду подстановки subs(,f), где в фигурных скобках указываются переменные хi и их новые значения аi (i=1,2,…), которые следует подставить в функцию f. Например:

Способ 2. Определение функции с помощью функционального оператора, который ставит в соответствие набору переменных (x1,x2,…) одно или несколько выражений (f1,f2,…). Например, определение функции двух переменных с помощью функционального оператора выглядит следующим образом:

Обращение к этой функции осуществляется наиболее привычным в математике способом, когда в скобках вместо аргументов функции указываются конкретные значения переменных. В продолжение предыдущего примера вычисляется значение функции:

Способ 3. С помощью команды unapply(expr,x1,x2,…), где expr – выражение, x1,x2,… – набор переменных, от которых оно зависит, можно преобразовать выражение expr в функциональный оператор. Например:

Какие операции оценивания производятся в Maple с действительными выражениями?

В Maple имеются следующие команды оценивания действительных выражений:

frac(expr) — вычисление дробной части выражения expr;

trunc(expr) — вычисление целой части выражения expr;

round(expr) — округление выражения expr;

Для чего предназначена команда evalf?

Все вычисления в Maple по умолчанию производятся символьно, то есть результат будет содержать в явном виде иррациональные константы, такие как, и другие. Чтобы получить приближенное значение в виде числа с плавающей запятой, следует использовать команду evalf(expr,t), где expr — выражение, t — точность, выраженная в числах после запятой.

С помощью каких команд можно найти вещественную и мнимую части комплексного выражения, а также его модуль и аргумент, и комплексно сопряженное ему число? Какую роль выполняет команда evalc?

Вещественную и мнимую части комплексного выражения z=x+iy можно найти с помощью команд Re(z) и Im(z). Например:

Если z=x+iy, то комплексно сопряженное ему выражение w=z*=x-iy можно найти с помощью команды conjugate(z). Продолжение предыдущего примера:

Модуль и аргумент комплексного выражения z можно найти с помощью команды polar(z), которую необходимо предварительно вызвать из стандартной библиотеки командой readlib. Например:

Если комплексное выражение очень сложное или содержит параметры, то команды Re(z) и Im(z) не дают требуемого результата. Получить вещественную и мнимую части комплексного выражения z можно, если использовать команду преобразования комплексных выражений evalc(z). (> evalc(Re(z)); evalc(Im(z));)

Источник

Использование оператора evalf()

Оператор evalf() в программе Maple используется для вычисления числовых значений выражений или функций с плавающей запятой. Этот оператор особенно полезен при работе с символьными выражениями, когда требуется получить численный результат.

Для использования оператора evalf() необходимо передать ему выражение или функцию, которые требуется вычислить. Оператор evalf() автоматически вычисляет значение выражения или функции с плавающей запятой с использованием точности по умолчанию.

Вот пример использования оператора evalf() в программе Maple:

В этом примере мы вычисляем квадратный корень из 2 с использованием оператора sqrt(). Затем мы передаем это выражение оператору evalf() и сохраняем результат в переменной result. Результат будет содержать числовое значение квадратного корня из 2.

Оператор evalf() также позволяет задать желаемую точность вычисления с помощью дополнительного параметра. Например:

В этом примере мы указываем оператору evalf() вычислить значение выражения с точностью до 10 десятичных знаков.

Использование оператора evalf() в программе Maple позволяет получать числовые значения для символьных выражений и функций с плавающей запятой, что может быть полезно при анализе и обработке данных.

В программе Maple можно легко вывести график функции для визуализации её поведения на плоскости. Для этого используется команда .

Синтаксис команды выглядит следующим образом:

• — выражение, представляющее функцию, которую нужно построить;
• — диапазон значений аргумента ;
• — дополнительные параметры графика (например, цвет, стиль линии и т.п.).

Например, чтобы вывести график функции в диапазоне от -5 до 5, можно использовать следующую команду:

После выполнения этой команды на экране появится график функции .