Теорема об умножении определителей

Примеры решения задач

Рассмотрим примеры решения задач связанных с рассмотренной теоремой. Читателю рекомендовано попытаться решить задачи самостоятельно, а затем сверить свое решение с приведенным ниже.

1. 1. Найти определитель произведения матриц: $$A=\begin{Vmatrix}3 & 4\\ 1 & -8\end{Vmatrix},
      B=\begin{Vmatrix}2 & 9\\ -1 & 5\end{Vmatrix}$$
      Решение

      Находим определители данных матриц второго порядка: $\begin{vmatrix}3 & -4\\ 1 & -6\end{vmatrix}=-18+4=-14
      $ и $\begin{vmatrix}2 & 7\\ 1 & 5\end{vmatrix}=10-7=3$. По теореме об определителе произведения матриц получаем: $$\det (A \cdot B)=\det \left (A \right ) \cdot \det \left ( B \right )=\left ( -14\right )\cdot\left ( 3 \right )=-42.$$ Вычислим этот же определитель, находя произведение матриц: $$A\cdot B=\begin{vmatrix}3 & -4\\ 1 & -6\end{vmatrix}\cdot\begin{vmatrix}2 & 7\\ 1 & 5\end{vmatrix}=\begin{vmatrix}2 & 1\\ -4 & -23\end{vmatrix}$$ Следовательно, $\det \left (A\cdot B\right )=-46+4=-42$. Результаты совпадают.

   2. Найти определитель матрицы пятого порядка: $$M=\begin{Vmatrix}
      1 & 2 & u & v & w\\3 & 4 & x & y & z\\0 & 0 & 3 & 2 & 1\\0 & 0 & 2 & 5 & 3\\0 & 0 & 3 & 4 & 2
      \end{Vmatrix}$$
      Решение

      Разобьём данную матрицу на 4 блока, $M=\begin{Vmatrix}A & B\\ O & C\end{Vmatrix}$ где $A=\begin{Vmatrix}1 & 2\\ 3 & 4\end{Vmatrix}$,
      $B=\begin{Vmatrix}u & v & w\\ x & y & z\end{Vmatrix}$, $O=\begin{Vmatrix}0 & 0 \\ 0 & 0\\ 0 & 0\end{Vmatrix}$, $C=\begin{Vmatrix}3 & 2 & 1\\ 2 & 5 & 3 \\3 & 4 & 2\end{Vmatrix}$.
      Представим блочную матрицу как произведение (в справедливости этого представления можно убедиться, найдя произведение по правилам умножения блочных матриц). $$D=\begin{Vmatrix}
      A & B\\C & D \end{Vmatrix} = \begin{Vmatrix} E_2 & O^T\\ O & C \end{Vmatrix} \cdot \begin{Vmatrix} E_2 & B\\ O & E_3 \end{Vmatrix} \cdot \begin{Vmatrix} A & O^T\\ O & E_3 \end{Vmatrix} ,$$ где $E_2,E_3$ — единичные матрицы соответствующих порядков.
      $\begin{vmatrix} A & O^T\\ O & E_3 \end{vmatrix} = \det A =\left | A \right |$, $\begin{vmatrix} E_2 & O^T\\ O & C \end{vmatrix} = \det C =\left | C \right|$.
      Матрица $\begin{Vmatrix} E_2 & B\\ O & E_3 \end{Vmatrix}$ — треугольная с единицами на главной диагонали, следовательно ее определитель равен $1$ По теореме об определителе произведения получаем:
      $$\begin{vmatrix} A & B\\ O & C \end{vmatrix}= \begin{vmatrix} E_2 & O^T\\ O & C \end{vmatrix}\ \cdot \begin{vmatrix} E_2 & B\\ O & E_3 \end{vmatrix}\ \cdot\begin{vmatrix} A & O^T\\ O & E_3
      \end{vmatrix}=\left | C \right |\cdot 1\cdot\left | A \right |=\left | A \right |\cdot\left | C \right |$$ Найдем $\det A$ и $\det C$. $\begin{vmatrix}1 & 2\\ 3 & 4\end{vmatrix}=-2$ $\begin{vmatrix}3 & 2 & 1\\ 2 & 5 & 3 \\3 & 4 & 2\end{vmatrix}=-15-8-36+30+18=-3$. Подставляя, получаем, $\det M=-2\cdot -3=-6$

   3. Представьте в виде определителя произведение определителей: $$\begin{vmatrix} 2 & 1 & 1 & 1\\ -1& 2 & 1 & 1\\ -1& -1& 2 & 1\\ -1&-1&-1& 2 \end{vmatrix}\cdot \begin{vmatrix} 4& 1\\ 1& 4 \end{vmatrix}\cdot\begin{vmatrix} -3 & 1\\ -1 & 3 \end{vmatrix}$$Решение

      По теореме об определителе ступенчатой матрицы имеем:
      $$\begin{vmatrix} 4& 1\\ 1& 4 \end{vmatrix}\cdot\begin{vmatrix} -3 & 1\\ -1 & 3 \end{vmatrix}=\begin{vmatrix} 4 & 1 & 0 & 0\\ 1 & 4 & 0 & 0\\ 0 & 0 & -3 & 1\\ 0 & 0 & -1 & 3 \end{vmatrix}$$ Предположим $$A=\begin{Vmatrix} 2 & 1 & 1 & 1\\ -1& 2 & 1 & 1\\ -1& -1& 2 & 1\\ -1&-1&-1& 2 \end{Vmatrix}, B=\begin{Vmatrix}
      4 & 1 & 0 & 0\\ 1 & 4 & 0 & 0\\ 0 & 0 & -3 & 1\\ 0 & 0 & -1 & 3
      \end{Vmatrix},$$
      тогда $$AB=\begin{Vmatrix} 9 & 6 & -4 & 4\\ -2 & 7 & -4 & 4\\ -5 & -5 & -7 & 5\\ -5 & -5 & 1 & 5 \end{Vmatrix},$$ по теореме об определителе произведения получаем искомый определитель $$\det
      (A\cdot B)=\begin{vmatrix} 9 & 6 & -4 & 4\\ -2 & 7 & -4 & 4\\ -5 & -5 & -7 & 5\\ -5 & -5 & 1 & 5 \end{vmatrix}.$$

Что такое определитель матрицы и как он применяется?

Определитель матрицы — это численное значение, которое можно вычислить для квадратной матрицы. Он играет важную роль в линейной алгебре и находит применение во множестве различных областей, включая физику, экономику и компьютерную графику.

Определитель матрицы обозначается символом det(A) или |A|. Для матрицы A размерности n x n определитель вычисляется следующим образом:

det(A) = a₁₁ * A₁₁ + a₁₂ * A₁₂ + … + a_1n * A_1n

где a_ij — элементы матрицы A, A_ij — алгебраическое дополнение элемента a_ij.

Определитель матрицы имеет несколько важных свойств:

• Определитель матрицы равен нулю тогда и только тогда, когда матрица вырождена, т.е. имеет линейно зависимые строки или столбцы.
• Если определитель матрицы равен нулю, то матрица не обратима.
• Определитель матрицы не изменяется при прибавлении к одной строке (столбцу) другой строки (столбца), умноженной на некоторое число.
• Определитель матрицы умножается на -1, если поменять местами две строки (столбца).
• Если матрицы A и B равны по всем элементам, кроме одного, то их определители также равны.

Определитель матрицы находит применение в различных задачах:

1. Решение систем линейных уравнений. Определитель матрицы используется для проверки того, имеет ли система единственное решение или есть бесконечное количество решений.
2. Нахождение обратной матрицы. Определитель матрицы используется для проверки обратимости матрицы и вычисления обратной матрицы.
3. Определение площади или объема. Определитель матрицы может быть использован для вычисления площади параллелограмма, образованного векторами в двумерном пространстве, или объема параллелепипеда, образованного векторами в трехмерном пространстве.
4. Вычисление определителя матрицы используется в теории вероятности, марковских процессах, а также в физике и экономике при моделировании систем и прогнозировании результатов.

Как видно из перечня применений, определитель матрицы является одним из ключевых понятий линейной алгебры и нашел широкое применение в многих областях знаний.

Свойства

• Определитель матрицы является алгебраическим инвариантом , из которого следует, что при заданной линейной карте все матрицы, которые ее представляют, будут иметь один и тот же определитель. Это позволяет определить значение определителя не только для матриц, но и для линейных отображений.
• Определитель матрицы и ее транспонированный совпадают:

Линейная карта между векторными пространствами обратима тогда и только тогда, когда ее определитель отличен от нуля . Следовательно, матрица с коэффициентами в поле обратима тогда и только тогда, когда ее определитель отличен от нуля.

Определитель продукта

Фундаментальным свойством определителя является его мультипликативное поведение относительно произведения матриц:

Это свойство важнее, чем кажется, и очень полезно при вычислении определителей. Действительно, предположим, что мы хотим вычислить определитель матрицы и что это любая матрица с определителем, равным единице (нейтральный элемент по отношению к произведению поля). В этом случае проверяют, что:

и аналогично ,

Линейное отображение между двумя конечномерными векторными пространствами может быть представлено матрицей. Матрица, связанная с композицией линейных отображений между конечномерными пространствами, может быть вычислена посредством произведения матриц. Для двух линейных отображений и выполняется следующее:

Блочные массивы

Пусть – матрицы размеров соответственно. затем

.

Это видно из формулы Лейбница . Используя следующее тождество

мы видим, что для обратимой матрицы A это

.

Точно так же подобное тождество можно получить с помощью факторинга.

Если это диагональные матрицы,

Производная детерминантной функции

Определяющая функция может быть определена на векторном пространстве, образованном квадратными матрицами порядка n . Указанное векторное пространство может быть легко преобразовано в нормированное векторное пространство с помощью матричной нормы , благодаря чему указанное пространство становится метрическим и топологическим пространством, в котором могут быть определены пределы. Определитель можно определить как морфизм алгебры матриц на множество элементов поля, на котором определены матрицы:

Дифференциал определяющей функции задается через сопряженную матрицу:

Где:

это массив вложений .

, является следом матрицы.

§ 4. Разложение определителя 3-го порядка по строке или столбцу

Определитель 3-го порядка равенсумме произведений элементов какой-нибудьстроки (или столбца) на их алгебраическиедополнения:

detA =

detA = + + - разложение по 1-й строке;

detA = + + - разложение по 2-й строке;

detA = + + - разложение по 3-й строке;

detA = + +- разложение по 1-му столбцу;

detA = + + - разложение по 2-му столбцу;

detA = + + - разложение по 3-му столбцу.

Пример.

Вычислить определитель: det A=

а) путем разложения по строке илистолбцу;

б) с использованием его свойств.

разложениепо 1-й строке: det A= 1(-4)+ 2(-8)+ 3(-10)= -4 -16 -30 = -50;

разложениепо 3-му столбцу: det A= 3(-10)+ 4(-5)+ 0(-5) = -30 -20 + 0 = -50.

с использованием его свойств:

detA = = =

= = = 1+ 0 + 0 = – 50

§ 5. Определители 4-го порядка

A= – матрица 4 -го порядка; – элементы матрицы (i= 1, … , 4; j = 1, … ,4).

Mij – минор элемента – это определитель матрицы 3 -гопорядка, полученной из данной матрицы 4 -го порядка путем вычеркивания i -той строки и j– того столбца:

 M11 =

 M23=

 M42= и т.д.

Aij – алгебраическое дополнениеэлемента :

A11= M11, A23= – M23, A42= M42,A34= – M34 и т.д.

Правило(выбора знака):

Пример. A =

A11= = = 2+ 0 − 3= −24 − 51 = −75

A23= − = = − (0 − 1+ 0) = = 8 − 0 = 8

A34= − = = − =

== − =

= = − (0 − 0 + 1)= −= −24

Теорема. Сумма произведений элементовкакой-нибудь строки (или столбца) на ихалгебраические дополнения есть величинапостоянная:

+ + + = + + + =

= + +  +  = + +  +  =

= + ++  = + +  +  =

= + + +  = + + + 

Определитель 4-го порядка – эточисло, равное сумме произведенийэлементов какой-нибудь строки (илистолбца) на их алгебраические дополнения:

detA = = + + + , i = 1, 2, 3, 4

или:

detA = = + ++ , j = 1, 2, 3, 4

Свойства определителей 4-го порядка- такие же, как и для определителей 2-го и 3-го порядков (свойства 1÷9).

Вычислениеопределителей 4-го порядка намногоупрощается, если разумно применитьсвойства определителей, например: получить много нулей в какой-нибудьстроке или столбце или привестиопределитель к треугольному виду.

Пример.

detA = = =

= = =

= = =0 + 0 + 0 + 1=

= = =

= = =

= = = 0 + 1+ 0 =

= −= −(135 + 44) = −179.

§ 6. Определители n-го порядка

A= – матрицаn –го порядка, – элементы матрицы (i= 1, 2, …, n; j= 1, 2, …, n).

Mij – минор элемента – это определитель матрицы (n– 1) – го порядка, полученной из даннойматрицы n– гопорядка путем вычеркивания i-той строки и j – тогостолбца.

Aij – алгебраическое дополнениеэлемента .

Теорема. Сумма произведенийэлементов какой-нибудь строки (илистолбца) матрицы n– го порядка на их алгебраическиедополнения есть величина постоянная:

+ + … +  = + ++ , i = 1, 2, … , n, j = 1, 2, …, n.

Определительn– го порядка – это число, равное суммепроизведений элементов какой-нибудьстроки (или столбца) матрицы n– го порядка на их алгебраическиедополнения:

detA = = + + … +  = + ++ ,

i = 1, 2, …, n, j =1, 2, …, n.

Свойства определителей n-гопорядка – такие же, как и для определителей 2-го, 3-го и 4-го порядков (свойства 1÷9).

Пример. Вычислить определитель n-го порядка: det A= .

Ко всемстрокам прибавим первую строку, умноженнуюна (-1):

det A= .

Получилиопределитель треугольной матрицы,который по свойству (9) равенпроизведению элементов, стоящих наглавной диагонали:

det A= 1()()… ()= ()()… ().

Пример. Вычислить определитель n-го порядка: det A= .

(Элементыглавной диагонали равны нулю, а всеостальные элементы равны 1).

Все строкиприбавим к первой строке:

det A=

Из первойстроки вынесем общий множитель:

det A= ()

Вычтемпервую строку из всех остальных строк:

detA = () = ().

Задачипо теме 1.

. Вычислитьопределители 2-го порядка (довестидо числового значения).

1. 2. 3.

4. 5. 6.

7. 8. 9.

10. 11. 12.

13. 14.

15. 16.

17. 18.

. Вычислитьопределители 3-го порядка:

− № 1 ÷ 8 – используя разложениепо строке или столбцу;

− № 9 ÷ 16 – используя свойстваопределителей.

1. 2. 3. 4.

5. 6. 7. 8.

9. 10. 11. 12.

13. 14. 15. 16.

. Вычислитьопределители 4-го порядка.

1. 2. 3.

4. 5. 6.

7. 8. 9.

Дополнительныезадачи.

1. Найтимногочлен: P(λ)= и вычислить его корни.

2. Дляматрицы A = вычислить: ++ … + и

+++,где i ≠ j (- алгебраическое дополнение элемента ).

Вычислитьопределители n-го порядка:

3. 4. 5.

6. 7.

8. 9.

10. 11. = min{i,j} 12. = max{i,j}

2. М А Т Р И ЦЫ

Калькулятор матриц с решением онлайн | Действия с матрицами

• Калькуляторы
• Калькулятор матриц – действия с матрицами онлайн

С помощью калькулятора матриц вы сможете выполнять различные преобразования матриц, решать СЛАУ, а также находить некоторые характеристики, как, например, определитель, след и ранг. Подробнее о функционале и использовании калькулятора смотрите после блока с самим калькулятором.

Также может быть интересно:

Как пользоваться калькулятором матриц

• В качестве элементов используются обыкновенные правильные дроби (1/2, 29/7, -1/125), десятичные дроби (12, -0.01, 3.14), а также числа в экспоненциальной форме (2.5e3, 1e-2).
• Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
• Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
• Вставляйте результат в A или B с помощью кнопок “Вставить в A” и “Вставить в B”.
• Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
• Используйте стрелки (←, ↑, →, ↓) для перемещения по элементам

С одной матрицей (только Матрица A или Матрица B)С двумя матрицами (Матрица A и Матрица B)

• Складывать;
• Вычитать;
• Умножать;
• Решать системы линейных алгебраических уравнений (СЛАУ) вида AX=B;
• Выполнять действия с выражениями, содержащими матрицы.

Вы можете вычислять различные арифметические выражения с матрицами, а также с результатами некоторых преобразований этих матриц.

Из чего могут состоять выражения?

• Целые и дробные числа
• Матрицы A, B
• Знаки арифметических действий: + – * /
• Круглые скобки для изменения приоритета операций: ( )
• Транспонирование: T
• Возведение в целую степень:

Примеры корректных выражений

• Cложение двух матриц: A+B, (A)+(B), ((A) + B)
• Возведение линейной комбинации матриц в степень: (3A – 0.5B)5
• Произведение транспонированной матрицы на исходную: ATA
• Обратная матрица в квадрате для B: B-2

Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами. Матрицы обозначаются заглавными латинскими буквами. При необходимости размер записывается следующим образом: An×m.

Некоторые теоретические сведения

Транспонирование — операция, при которой строки и столбцы матрицы меняются местами: aTij = aji

диагональ квадратной матрицы — диагональ, которая проходит через верхний левый и нижний правый углы. Элементы главной диагонали — aii

Единичная матрица En×n — квадратная матрица из n столбцов и n строк с единицами на главной диагонали и нулями вне её.

Ранг — это максимальное количество линейно независимых строк (столбцов) этой матрицы. Обозначение: rank(A)

След — это сумма элементов, находящихся на её главной диагонали. Обозначение: tr(A) или track(A)

Умножение матрицы на число — матрица такой же размерности, что и исходная, каждый элемент которой является произведением соответствующего элемента исходной матрицы на заданное число.

Возведение в степень — умножение заданной матрицы саму на себя n-ое количество раз, где n – степень, в которую необходимо возвести исходную матрицу. Обозначение: An

Обратная матрица A−1 — матрица, произведение которой на исходную матрицу A равно единичной матрице: A-1×A = A×A-1 = E

Треугольная матрица — квадратная матрица, у которой выше (верхнетреугольная матрица) или ниже (нижнетреугольная матрица) главной диагонали находятся нули.

LU-разложение — представление матрицы в виде произведения двух матриц L и U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица. A = L·U

Сложение матриц An×m и Bn×m — матрица Cn×m, получаемая попарной суммой соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: сij=aij+bij

Разность матриц An×m и Bn×m — матрица Cn×m, получаемая попарной разностью соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен: сij=aij-bij

Умножение матриц An×k и Bk×m — матрица Cn×m, у которой элемент (cij) равен сумме произведений элементов i-той строки матрицы A на соответствующие элементы j-того столбца матрицы B: cij = ai1·b1j + ai2·b2j + … + aik·bkj

Определитель 4 порядка. Калькулятор

Определители четвертого и старших порядков возможно вычислять по упрощенным схемам, которые заключаются в разложении по элементам строк или столбцов или сведении к треугольному виду. Оба метода для наглядности будут рассмотрены на матрицах 4-го порядка.

Метод разложения по элементам строк или столбцов

Первый пример мы рассмотрим с подробными объяснениями всех промежуточных действий.

Пример 1. Вычислить определитель методом разложения.

Решение. Для упрощения вычислений разложим определитель четвертого порядка по элементам первой строки (содержит нулевой элемент). Они образуются умножением элементов на соответствующие им дополнения (образуются вычеркивания строк и столбцов на пересечении элемента, для которого исчисляются – выделено красным)

В результате вычисления сведутся к отысканию трех определителей третьего порядка, которые находим по правилу треугольников

Найденные значения подставляем в выходной детерминант

Результат легко проверить с помощью матричного калькулятора YukhymCALC . Для этого в калькуляторе выбираем пункт Матрицы-Определитель матрицы, размер матрицы устанавливаем 4*4.

Далее вводим же матрицу и осуществляем вычисления. Результатом расчетов будет следующий вывод данных

Результаты совпадают, следовательно вычисления проведены верно.

Пример 2. Вычислить определитель матрицы четвертого порядка.

Решение.

Как и в предыдущем задании осуществим вычисления методом разложения. Для этого выберем элементы первого столбца. Упрощенно определитель можно подать через сумму четырех детерминант третьего порядка в виде

Далее переходим к отысканию определителей по правилу треугольников

Результат проверяем матричным калькулятором YukhymCALC . Правильность расчетов подтверждается следующим рисунком

Метод возведения определителя к треугольному виду

Данный метод позволяет ряд определителей вычислить достаточно быстрый способ. Суть его заключается в объединении определителя к треугольному виду, при этом следует учитывать все множители на которые увеличиваем или уменьшаем строки и учете при конечных расчетах. Из данного определения Вы ничего для себя не поймете, поэтому лучше все показать на конкретных примерах.

Пример 3. Найти определитель матрицы сведением к треугольному виду

Решение.

Сначала осуществляем математические манипуляции, чтобы получить все нулевые элементы кроме первого в первом столбце. Для этого от второй строки вычитаем первый, умноженный на два. В результате получим

Дальше целесообразнее от четвертой отнять удвоенную вторую строчку. В результате элементарных преобразований определитель примет вид

Осталось превратить в ноль один элемент в третьем столбце. Для этого от четвертой строки вычитаем удвоенную третью в предварительно записанном определителе

По свойству, определитель треугольной матрицы равен произведению диагональных элементов.

По желанию можно проверить результат матричным калькулятором.

Рассмотрим более сложный.

Пример 4.

Найти определитель матрицы 4-го порядка

Решение.

Элементарными преобразованиями сводим определитель к треугольного вида. Для этого от каждой строки вычитаем первый. В результате преобразований получим следующий детерминант

Для удобства вычислений, меняем третью строчку со вторым местами..

По свойству определителей любая замена строк местами ведет к изменению знака определителя. Учитываем это в некотором множителе k=-1.

От третьей строки вычитаем второй, умноженный на минус три. После упрощений получим

Результат будет следующим

От удвоенного четвертой строки вычитаем третий. По свойству, умножения строки на постоянную а ведет к изменению определителя в а раз. Данное изменение фиксируем в множителе k=-1*2=-2.

Окончательное значение определителя будет равно произведению диагональных элементов разделенных (или нормированных) на множитель k, который отвечает за изменение детерминанта при элементарных преобразованиях. Выполняем вычисления

Проверка матричным калькулятором подтверждает правильность производимых вычислений.

В других случаях нужно пользоваться комбинацией этих методов, в последнее образовывать как можно больше нулевых элементов, а методом разложения по строкам или столбцам уменьшать количество выполненных операций.

Это позволит без проблем вычислять определители третьего, четвертого и даже пятого порядка.

Определитель матрицы 4 порядка

Определение

Матрица представляет собой прямоугольную таблицу скаляров, то есть элементов некоторого поля, которая состоит из определенного числа столбцов и определенного числа строк.

Существует разные типы матриц

При рассмотрении данной темы важно уточнить понятия некоторых из них:

• в том случае, когда матрица обладает единственным элементом, она является совпадающей со своим единственным скаляром;
• квадратная матрица представляет собой такую матрицу, которая имеет равное число столбцов и строк.

Алгебраические действия с матрицами характеризуются определенным алгоритмом и порядком. Подобные операции отличаются от манипуляций с простыми числами. Кроме алгебраических действий, над матрицами выполняют и другие операции. К примеру, транспортирование матрицы.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

В задачах часто встречаются примеры нахождения определителя матриц разных порядков. Матрицы первого, второго, третьего, четвертого и других порядков относят к квадратным матрицам.

Определение

Определитель или детерминант матрицы является определенным числом, которое можно поставить в соответствие некой квадратной матрице.

В том случае, когда элементы матрицы имеют вид действительных чисел, то и определитель является действительным числом. Определитель обозначают detA или |A|. Определитель первого порядка соответствует скаляру рассматриваемой матрицы.

Определители второго и третьего порядка определяются в соответствии со стандартным алгоритмом, то есть с помощью известных формул. Для того чтобы вычислить определитель больше третьего порядка, требуется ознакомиться с понятием минора матрицы (М).

Определение

Минор матрицы третьего порядка является определителем второго порядка, который получен из заданной матрицы третьего порядка путем вычеркивания i-ой степени и j-го столбца.

Примечание

Изучая материалы по теме матричного определителя, можно встретить термин «детерминант». Фактически данные понятия идентичны. Однако детерминант обладает множеством значений в других научных областях, что объясняет использование его русского перевода в математике.

Свойства определителя:

• при перестановке местами двух строк или столбцов знак определителя меняется;
• при умножении строки или столбца на число, весь определить также умножится на число;
• в том случае, когда одну строку сколько угодно раз прибавляют или вычитают из другой, определитель не меняется;
• при наличии одинаковых, пропорциональных или заполненных нулями двух строк определителя весь определитель равен нулю;
• все перечисленные свойства справедливы в случае столбцов;
• транспортирование матрицы не сопровождается изменением определителя;
• определитель произведения матриц равен произведению определителей.

Геометрическая интерпретация детерминанта

Детерминант — это величина, которая вычисляется для квадратной матрицы и содержит информацию о свойствах этой матрицы. Геометрическая интерпретация детерминанта позволяет понять, какие геометрические преобразования происходят с векторами при умножении на данную матрицу.

Главным образом, геометрическая интерпретация детерминанта связана с понятием площади (в двумерном случае) или объема (в трехмерном случае). Детерминант положительный, если он соответствует положительной площади или объему, и отрицательный, если он соответствует отрицательной площади или объему.

Для многих матриц геометрическая интерпретация детерминанта имеет простую и интуитивно понятную форму. Например, для двумерной матрицы следующие значения детерминанта имеют следующие геометрические интерпретации:

• Детерминант равен 0, если матрица преобразует множество векторов в множество векторов нулевой площади.
• Детерминант положителен, если матрица увеличивает площадь множества векторов.
• Детерминант отрицателен, если матрица отражает множество векторов именно тогда, когда относительный порядок горизонтального и вертикального направлений меняется.

В трехмерном случае геометрическая интерпретация детерминанта также связана с объемом:

• Детерминант равен 0, если матрица преобразует множество векторов в множество векторов нулевого объема.
• Детерминант положителен, если матрица увеличивает объем множества векторов.
• Детерминант отрицателен, если матрица отражает множество векторов именно тогда, когда изменяется ориентация пространства.

Геометрическая интерпретация детерминанта позволяет лучше понять свойства матриц и их влияние на пространственные преобразования

Это важное понятие в линейной алгебре и используется во многих областях науки и инженерии

Вычисление определителя ручным способом

Определителем матрицы первого порядка, или определителем первого порядка, называется элемент а11:

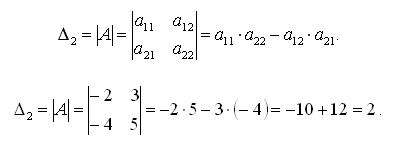
Определить количество слагаемых, для нахождения определителя матрицы, в алгебраической сумме, можно вычислив факториал:

Матрица 1-го порядка	1! = 1
Матрица 2-го порядка	2! = 1 × 2 = 2
Матрица 3-го порядка	3! = 1 × 2 × 3 = 6
Матрица 4-го порядка	4! = 1 × 2 × 3 × 4 = 24
Матрица 5-го порядка	5! = 1 × 2 × 3 × 4 × 5 = 120 …

Свойства определителей матриц Свойство № 1: Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А|Т Свойство № 2: При перестановке 2-х строк или столбцов матрицы ее определитель изменит знак на противоположный, сохраняя абсолютную величину. 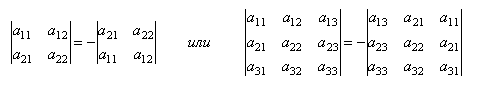Свойство № 3: Определитель матрицы, имеющий два одинаковых ряда, равен нулю. Свойство № 4: Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.

Следствия из свойств № 3 и № 4: Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю. Свойство № 5: Если все элементы какой–либо строки или столбца определителя матрицы равны нулю, то сам определитель матрицы равен нулю. Свойство № 6: Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-х определителей по формуле: 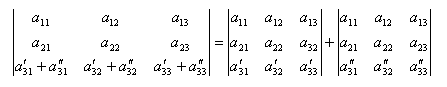Свойство № 7: Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.

Пример 1. Вычислить определитель произведения матриц A и B.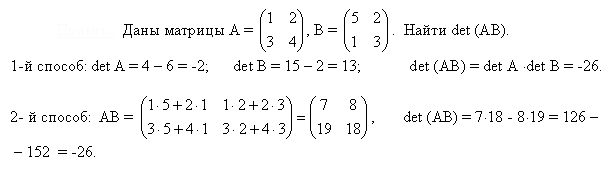

Вычисление определителя с помощью Excel
В Excel для вычисления определителя квадратной матрицы используется функция МОПРЕД. Функция имеет видМОПРЕД(массив).
Здесь массив – это числовой массив, в котором хранится квадратная матрица. При этом массив может быть задан как интервал ячеек, например, A1:C3, или как массив констант, например, {1;2;3: 4;5;6: 7;8;9}.

Пример 2. Найти определитель матрицы .

Ход решения:

1. Введите матрицу (рис.1)

Рисунок 1. Матрица А

1. Курсор поставьте в ячейку, в которой необходимо получить значение определителя, например в A4.
2. Вызовите Мастер функции и в категории «Полный алфавитный перечень» найдите функцию МОПРЕД. После этого щелкните ОК.
3. В появившемся окне укажите диапазон (A1:C3), в котором находится матрица, и нажмите ОК.
4. В результате в ячейке появится значение определителя матрицы = 6.

Задание 1:  вычислить с помощью Excel определитель из примера 1.Задание 2:  вычислить с помощью Excel определитель из семестрового задания по своему варианту.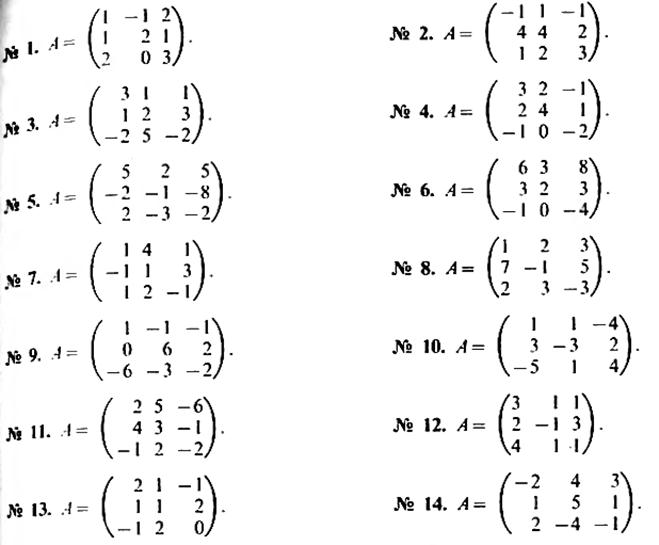

Составитель: Салий Н.А.