Как найти периметр основания пирамиды?

Связь пирамиды с цилиндром

Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.

Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.

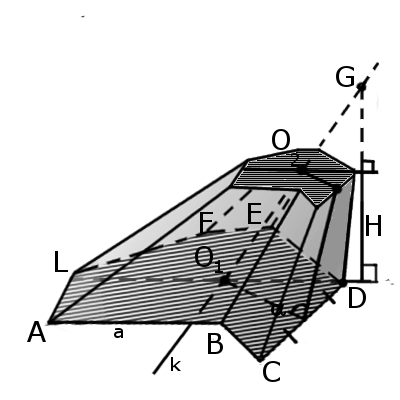
Усеченная пирамида (пирамидальная призма)

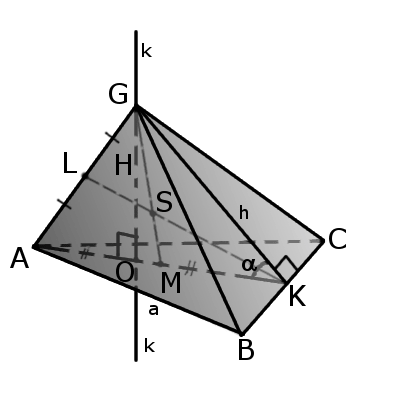
Треугольная пирамида (четырехгранник)

В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.

Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол
.

Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника
(GM).

Бимедианой
называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).

Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.

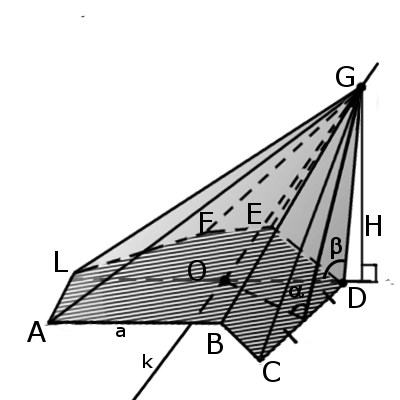
Наклонная пирамида
тупой угол

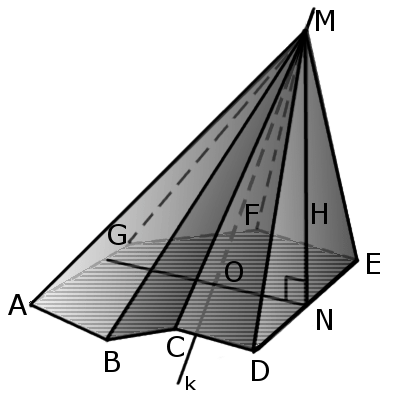
Прямоугольная пирамида

Определение.
Остроугольная пирамида
— это пирамида в которой апофема больше половины длины стороны основания.

Определение.
Тупоугольная пирамида
— это пирамида в которой апофема меньше половины длины стороны основания.

Определение.
Правильный тетраэдр
— четырехгранник у которого все четыре грани — равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.

Определение.
Прямоугольный тетраэдр
называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол
и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.

Определение.
Равногранный тетраэдр
называется четырехгранник у которого боковые грани равны между собой, а основание — правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.

Определение.
Ортоцентричный тетраэдр
называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.

Определение.
Звездная пирамида
называется многогранник у которого основой является звезда.

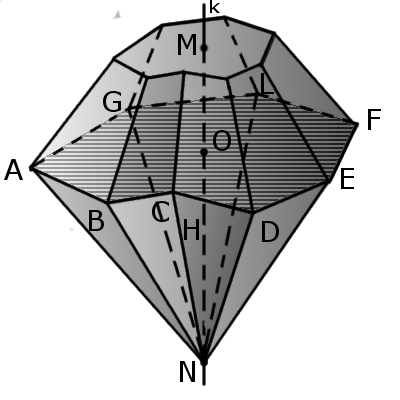
Бипирамида
общую основу

При подготовке к ЕГЭ по математике учащимся приходится систематизировать знания по алгебре и геометрии. Хочется объединить все известные сведения, например, о том, как вычислить площадь пирамиды. Причем начиная от основания и боковых граней до площади всей поверхности. Если с боковыми гранями ситуация ясна, так как они являются треугольниками, то основание всегда разное.

Важность расчета периметра для архитектуры и строительства

Корректный расчет периметра позволяет определить не только размеры основания пирамиды, но и общую площадь, которую она будет занимать. Это позволяет архитекторам и строителям более точно планировать расположение и размеры зданий, а также правильно оценивать необходимое количество материалов для возведения пирамиды.

Точный расчет периметра также позволяет предотвратить возможные ошибки и искажения в форме пирамиды. Правильная форма основания обеспечивает устойчивость и прочность всей конструкции, а также правильное распределение нагрузки на все ее элементы.

Кроме того, знание периметра основания пирамиды позволяет провести дополнительные расчеты для определения объема ее внутреннего пространства и площади боковой поверхности

Это очень важно для планирования размещения помещений внутри пирамиды и определения ее функционального назначения

Суммируя, можно сказать, что расчет периметра основания пирамиды является неотъемлемой частью архитектурного и строительного процесса.
Точный расчет периметра позволяет определить размеры и форму основания пирамиды, а также правильно планировать расположение и размеры зданий.
Расчет периметра помогает предотвратить возможные ошибки и искажения в форме пирамиды, обеспечивая ее устойчивость и прочность.
Знание периметра позволяет провести дополнительные расчеты для определения объема и площади боковой поверхности пирамиды, что важно для планирования внутреннего пространства.

В данной статье были рассмотрены методы нахождения периметра основания пирамиды, если известна площадь. Оказалось, что периметр может быть найден, основываясь на формуле, которая связывает площадь основания и периметр. Это очень полезно при решении задач, связанных с построением и измерением пирамид.

В первом методе была представлена формула для нахождения периметра основания пирамиды по известной площади. Второй метод позволял найти периметр, основываясь на формуле для площади, подставленной в уравнение периметра.

Кроме того, было отмечено, что нахождение периметра основания пирамиды является важным шагом при решении задач, связанных с вычислениями и измерениями. Правильное нахождение периметра поможет получить точные и достоверные результаты.

Итак, нахождение периметра основания пирамиды по известной площади является важным и полезным навыком, который может быть применен при решении различных задач и измерений.

Выбор основания

Основание пирамиды может быть любой фигурой, с данными свойствами:

1. Плоскость: Основание должно быть плоским, чтобы пирамида могла устоять на нем. Плоскость основания должна быть гладкой и ровной.

2. Форма: Основание может быть треугольным, четырехугольным, пятиугольным, шестиугольным и т.д

Важно учитывать, что форма основания будет также определять форму боковых граней пирамиды

3. Размеры: Основание может иметь разные размеры, включая длину сторон или радиус, в зависимости от выбранной фигуры. Размеры основания также будут влиять на высоту пирамиды.

При выборе основания следует учитывать цель построения пирамиды и ее внешний вид. Основание может быть выбрано в соответствии с тем, какую информацию или идею нужно представить, а также в зависимости от условий задачи.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

• Перевести мм² в см². Введите площадь в квадратных миллиметрах, калькулятор переведет её в кв. сантиметры.
• Перевести м² в см². Введите площадь в квадратных метрах, калькулятор переведет её в квадратные сантиметры.
• Перевести кв. дюймы в квадратные см². Введите площадь в квадратных дюймах, калькулятор переведет её в квадратные сантиметры.
• Перевести кв. футы в кв. метры. Введите площадь в квадратных футах, калькулятор переведет её в квадратные метры.
• Перевести кв. мили в км². Введите площадь в квадратных милях, калькулятор переведет её в километры квадратные.
• Перевести акры в м². Введите площадь в акрах, калькулятор переведет её в квадратные метры.
• Перевести акры в сотки. Введите площадь в акрах, калькулятор переведет её в сотки.
• Перевести гектары в акры. Введите площадь в гектарах, калькулятор переведет её в акры.
• Перевести акры в гектары. Введите площадь в акрах, калькулятор переведет её в гектары.
• Перевести квадратные метры в акры. Введите площадь в квадратных метрах, калькулятор переведет её в акры.

Виды фигуры

Пирамида – геометрическая фигура, обозначающая и представляющая собой несколько граней. По сути – это тот же многогранник, в основании которого лежит многоугольник, а по бокам расположены треугольники, соединяющиеся в одной точке – вершине. Фигура бывает двух основных видов:

• правильная;
• усечённая.

В первом случае, в основании лежит правильный многоугольник. Тут все боковые поверхности равны между собой и сама фигура порадует глаз перфекциониста.

Во втором случае, оснований два — большое в самом низу и малое между вершиной, повторяющее форму основного. Иными словами – усечённая пирамида представляет собой многогранник с сечением, образованным параллельно основанию.

Задача № 3

Условие
. У правильной четырехугольной пирамиды необходимо вычислить площадь. В ней известна сторона квадрата — 6 см и высота — 4 см.

Решение.
Проще всего воспользоваться формулой с произведением периметра и апофемы. Первое значение найти просто. Второе немного сложнее.

Придется вспомнить теорему Пифагора и рассмотреть Он образован высотой пирамиды и апофемой, которая является гипотенузой. Второй катет равен половине стороны квадрата, поскольку высота многогранника падает в его середину.

Искомая апофема (гипотенуза прямоугольного треугольника) равна √(3 2 + 4 2) = 5 (см).

Теперь можно вычислять искомую величину: ½*(4*6)*5+6 2 = 96 (см 2).

Ответ.
96 см 2 .

Термины и обозначения

Основные термины:

• Правильный (равносторонний) треугольник – фигура с тремя одинаковыми углами и равными сторонами. В этом случае все углы имеют 60 градусов. Фигура является простейшей из правильных многогранников. Если эта фигура лежит в основании, то такой многогранник будет называться правильной треугольной. Если в основании лежит квадрат, пирамида будет называться правильной четырёхугольной пирамидой.
• Вершина – самая верхняя точка, где сходятся грани. Высота вершины образуется прямой линией, исходящей от вершины к основанию пирамиды.
• Грань – одна из плоскостей многоугольника. Она может быть в виде треугольника в случае с треугольной пирамидой либо в виде трапеции для усечённой пирамиды.
• Сечение – плоская фигура, образующаяся в результате рассечения. Не стоит путать с разрезом, так как разрез показывает и то, что находится за сечением.
• Апофема – отрезок, проведённый из вершины пирамиды к её основанию. Он также является высотой той грани, где находится вторая точка высоты. Данное определение справедливо лишь по отношению к правильному многограннику. К примеру – если это не усечённая пирамида, то грань будет представлять собой треугольник. В данном случае высота этого треугольника и станет апофемой.

Расчет площади и периметра основания

Расчет площади основания

Площадь основания пирамиды зависит от его формы. В случае, если основание является прямоугольником, площадь можно найти по формуле: S = a * b, где a и b – длины сторон прямоугольника.

Если основание представляет собой круг, то площадь можно рассчитать по формуле: S = π * r^2, где π – математическая константа, равная приблизительно 3.14, а r – радиус круга.

Если основание является треугольником, то площадь можно найти с помощью формулы Герона: S = √(p * (p — a) * (p — b) * (p — c)), где p – полупериметр треугольника, равный полусумме его сторон (p = (a + b + c) / 2).

Расчет периметра основания

Периметр основания пирамиды также зависит от его формы. Для прямоугольника периметр можно найти по формуле: P = 2*a + 2*b, где a и b – длины сторон прямоугольника.

Для круга периметр не определяется, так как круг не обладает сторонами и периметром.

Для треугольника периметр равен сумме длин его сторон: P = a + b + c.

Существует несколько способов измерения высоты пирамиды:

1. Измерение с использованием правильных сечений. При этом пирамида разрезается в горизонтальной плоскости параллельно основанию и полученное сечение может быть рассмотрено как основание плоской фигуры. Высота этой фигуры будет равна высоте пирамиды.
2. Измерение с использованием подобных пирамид. При этом строится подобная пирамида, основание которой совпадает с основанием исходной пирамиды, а вершины соединены проведенной внутри пирамиды прямой. Высота подобной пирамиды будет равна высоте исходной пирамиды.
3. Измерение с использованием геометрических расчетов. При этом применяются теоремы и формулы геометрии для определения высоты пирамиды на основе известных параметров, таких как угол между боковыми гранями, длины ребра основания и площадь основания.

В завершение стоит отметить, что высота пирамиды является одним из важнейших параметров, так как она используется для определения объема пирамиды и выполнения различных геометрических расчетов.

Пирамида

Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д. Пирамида является частным случаем конуса.

Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:

• боковые рёбра правильной пирамиды равны;
• в правильной пирамиде все боковые грани — конгруэнтные равнобедренные треугольники;
• в любую правильную пирамиду можно как вписать, так и описать вокруг неё сферу;
• если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна Пи, а каждый из них соответственно Пи/n, где n — количество сторон многоугольника основания;
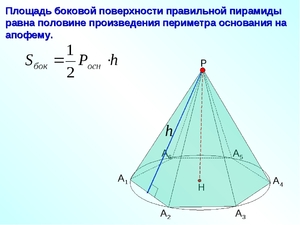
• площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Плюсы и минусы каждого из способов

При вычислении высоты пирамиды по боковому ребру и основанию существуют различные подходы, каждый из которых имеет свои плюсы и минусы:

1. Метод геометрической фигуры

• Плюсы: данный метод является наиболее простым и понятным, не требует использования сложных формул и комплексных вычислений.
• Минусы: не всегда возможно точно определить или измерить угол наклона бокового ребра пирамиды, что может привести к неточному результату. Также, данный метод позволяет вычислить высоту пирамиды только при известном боковом ребре и основанию.

Метод теоремы Пифагора

• Плюсы: данный метод основан на известной математической теореме и позволяет вычислить высоту пирамиды при известном боковом ребре и основании, поэтому его можно применять в широком спектре задач.
• Минусы: использование данного метода требует знания и умения применять теорему Пифагора, что может создать сложности для некоторых людей. Также, в некоторых случаях результат может быть неточным из-за округления чисел при вычислениях.

Выбор конкретного метода зависит от задачи и доступной информации

Важно учитывать преимущества и недостатки каждого метода для получения наиболее точного результата

Установление точек

Для начертания пирамиды в геометрии необходимо установить точки на плоскости или в пространстве. Это позволит определить расположение вершин и ребер пирамиды.

Перед началом установления точек необходимо определить плоскость или координатную систему, в которой будет рассматриваться пирамида. В плоскости необходимо выбрать точку, которая будет соответствовать вершине пирамиды. В трехмерном пространстве нужно выбрать три точки, которые будут образовывать треугольник или другую плоскую форму, с которой будет начерчена пирамида.

Установка точек может осуществляться как с помощью инструментов графического редактора, так и с помощью координатных осей. Для установки точек с использованием координатных осей необходимо указать значения координат, задающие положение точек на плоскости или в пространстве.

При установке точек следует учитывать, что расстояние между вершинами пирамиды должно быть реалистичным и соответствовать замыслу автора или требованиям задачи

Важно также установить точки по таким правилам, чтобы пирамида была устойчивой и симметричной

После того как точки установлены, можно приступать к соединению их ребрами с помощью линий или соединяемой плоскости. Таким образом, будет закончена начертательная часть пирамиды.

В чем преимущество пирамиды

Пирамида — многогранник, основание которого является многоугольником, а остальные грани — треугольниками, имеющими общую вершину.

Пирамидальная форма имеет несколько преимуществ:

1. Стабильность. Пирамида имеет широкое основание и суживающийся верх, что делает ее очень стабильной. Это свойство делает пирамиду идеальным выбором для многих инженерных и архитектурных конструкций.
2. Эффективность использования пространства. Пирамидальная форма позволяет использовать пространство более эффективно. Благодаря своей форме пирамида может поместить больше материала на меньшей площади, чем другие формы.
3. Видимость. Пирамиды обычно имеют значительную высоту и суживающуюся вершину, что делает их легко заметными издалека. Это свойство делает пирамиды идеальным выбором для монументальных сооружений, таких как пирамиды в Египте или Латинской Америке.
4. Эстетика. Пирамидальная форма может быть очень эстетичной и привлекательной. Она может использоваться в различных областях, таких как дизайн зданий, декоративное искусство, упаковка продуктов и многое другое.

В целом, пирамидальная форма имеет множество преимуществ, которые делают ее полезной в различных областях. Однако, как и любая другая форма, она может иметь свои недостатки в зависимости от контекста, в котором она используется.

Задача № 4

Условие.
Дана правильная Стороны ее основания равны 22 мм, боковые ребра — 61 мм. Чему равна площадь боковой поверхности этого многогранника?

Решение.
Рассуждения в ней такие же, как были описаны в задаче №2. Только там была дана пирамида с квадратом в основании, а теперь это шестиугольник.

Первым делом вычисляется площадь основания по указанной выше формуле: (6*22 2) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 см 2 .

Теперь необходимо узнать полупериметр равнобедренного треугольника, который является боковой гранью. (22+61*2):2 = 72 см. Осталось по формуле Герона сосчитать площадь каждого такого треугольника, а потом умножить ее на шесть и сложить с той, что получилась для основания.

Расчеты по формуле Герона: √(72*(72-22)*(72-61) 2)=√435600=660 см 2 . Вычисления, которые дадут площадь боковой поверхности: 660*6 = 3960 см 2 . Осталось их сложить, чтобы узнать всю поверхность: 5217,47≈5217 см 2 .

Ответ.
Основания — 726√3 см 2 , боковой поверхности — 3960 см 2 , вся площадь — 5217 см 2 .

Треугольной пирамидой
называется многогранник, в основании которого лежит правильный треугольник.

В такой пирамиде грани основания и ребра боковых сторон равны между собой. Соответственно площадь боковых граней находится из суммы площадей трех одинаковых треугольников. Найти площадь боковой поверхности правильной пирамиды можно по формуле . А можно произвести расчет в несколько раз быстрее. Для этого необходимо применить формулу площади боковой поверхности треугольной пирамиды:

где p
– периметр основания, у которого все стороны равны b, a
– апофема, опущенная из вершины к этому основанию. Рассмотрим пример расчета площади треугольной пирамиды.

Задача: Пусть дана правильная пирамида. Сторона треугольника, лежащего в основании равна b
= 4 см. Апофема пирамиды равна a
= 7 см. Найдите площадь боковой поверхности пирамиды.
Так как по условиям задачи мы знаем длины всех необходимых элементов, найдем периметр. Помним, что в правильном треугольнике все стороны равны, а, следовательно, периметр рассчитывается по формуле:
Подставим данные и найдем значение:
Теперь, зная периметр, можем рассчитывать площадь боковой поверхности:

Чтобы применить формулу площади треугольной пирамиды для вычисления полного значения, необходимо найти площадь основания многогранника. Для этого используется формула :
Формула площади основания треугольной пирамиды может быть и другой. Допускается применение любого расчета параметров для заданной фигуры, но чаще всего это не требуется. Рассмотрим пример расчета площади основания треугольной пирамиды.

Задача: В правильной пирамиде сторона лежащего в основании треугольника равняется a
= 6 см. Рассчитайте площадь основания.
Для вычисления нам требуется только длина стороны правильного треугольника, располагающегося в основании пирамиды. Подставим данные в формулу:

Довольно часто требуется найти полную площадь многогранника. Для этого потребуется сложить площадь боковой поверхности и основания.
Рассмотрим пример расчета площади треугольной пирамиды.

Задача: пусть дана правильная треугольная пирамида. Сторона основания равна b
= 4 см, апофема a
= 6 см. Найдите полную площадь пирамиды.
Для начала найдем площадь боковой поверхности по уже известной формуле. Рассчитаем периметр:
Подставляем данные в формулу:
Теперь найдем площадь основания: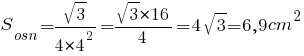
Зная площадь основания и боковой поверхности, найдем полную площадь пирамиды:

При расчете площади правильной пирамиды стоит не забывать о том, что в основании лежит правильный треугольник и многие элементы этого многогранника равны между собой.

Определение.
Боковая грань
— это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).

Определение.
Боковые ребра
— это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.

Определение.
Высота пирамиды
— это перпендикуляр, опущенный из вершины на основание пирамиды.

Определение.
Апофема
— это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.

Определение.
Диагональное сечение
— это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.

Определение.
Правильная пирамида
— это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.

Где можно применить калькулятор объема пирамиды

Калькулятор объема пирамиды можно применить в различных сферах, где требуется вычислить объем пирамиды, например:

1. Строительство: при проектировании зданий и сооружений инженерам и архитекторам часто нужно вычислить объем пирамиды, например, для расчета объема кровли или фундамента.
2. Геометрия: в математике пирамиды являются важным объектом изучения, и вычисление их объема — одна из основных задач геометрии.
3. Производство: в производстве может потребоваться вычислить объем пирамиды для расчета необходимых материалов, например, для производства упаковки.
4. Учебные цели: калькулятор объема пирамиды может быть использован студентами и учениками при изучении геометрии или математики.
5. Игры и развлечения: калькулятор объема пирамиды может быть использован в играх и развлечениях, где требуется решить задачу по вычислению объема пирамиды.

В целом, калькулятор объема пирамиды может быть полезен во всех ситуациях, где требуется вычислить объём данной фигуры.