Вычисление тригонометрических функций числа
В данном пункте рассмотрим случай, когда определение рассматриваемых нами функций тригонометрии, происходит из числового значения, а не угла. Таких подходов два:
- Sin, cos, tg, ctg числа n, является число которое равно sin, сos, tg, ctg n радиан. Где Радиа́н это угол, который соответствует дуге, которая в свою очередь равна длине, её радиуса. Пример: sin числа2k=sin угла2k радиан. Используя формулы можно получить таблицу часто встречаемых углов, которая поможет быстро перевести значения из градусов в радианы и в противоположную сторону.
- На прямоугольной системе координат, в единичной окружности, ставится точка, которой соответствует любое действительное значение числа d. тригонометрические функции можно определить, узнав координаты этой точки.
- Считая начальной точкой А с координатами (1,0). Поэтому для того чтобы найти взаимодействие между точкой на окружности и числом, нужно найти отрицательное и положительное значение числа d, положительным будет значение при движении точки А(1,0) в противоположную сторону движения часовой стрелки и её движение будет равным open t \ t, а отрицательным движение по часовой стрелке.
В связи с этим выделяют следующие функции:
- (sin f = y) Синус числа f- определяется ординатой точки единичной окружности, которая равна числу f;
- (cos f = x) Косинус числа f — абсцисса окружности, которая соответствующая числу f;
- (tg f = y\x=sin f\cos f) тангенс f определяется делением ординаты на абсциссу точки, равной числу f.
Примеры применения синуса угла
- Геометрия: синус угла позволяет вычислить длину стороны непрямоугольного треугольника по известным углам и другим сторонам. Это полезно, например, при решении задач на построение треугольников или при нахождении высоты горы по углу наблюдения.
- Физика: синус угла используется при расчете силы, действующей на наклонную плоскость или при определении коэффициента трения между двумя поверхностями. Также, синус угла применяется при анализе колебаний и волн, например, при определении амплитуды звука или света.
- Техника: синус угла применяется при проектировании и расчете механизмов, таких как краны, грузоподъемные механизмы или мосты. Синус угла позволяет определить необходимую длину стрелы крана или расчетную нагрузку на мостовую конструкцию при заданном угле наклона.
- Астрономия: синус угла применяется при изучении небесных тел, например, при определении высоты или азимута наблюдаемого объекта. Синус угла позволяет точно определить положение звезды или планеты на небесной сфере.
- Медицина: синус угла применяется при измерении артериального давления или угла наклона костей при диагностике различных заболеваний или травм.
Это лишь некоторые примеры использования синуса угла. Функция синуса является одной из основных математических функций и имеет широкий спектр применений в разных областях.
Теорема синусов, теорема косинусов
Теорему Пифагора и тригонометрические функции острого угла можно использовать для вычисления элементов только в прямоугольном треугольнике.
Для нахождения элементов в произвольном треугольнике используется теорема синусов или теорема косинусов.
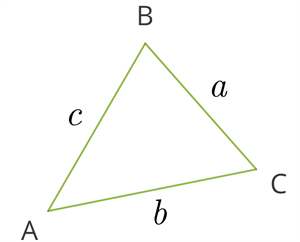
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов:
a sinA = b sinB = c sinC
(в решении задачи одновременно пишутся две части, они образуют пропорцию).
Теорема синусов используется для вычисления:
неизвестных сторон треугольника, если даны два угла и одна сторона;
неизвестных углов треугольника, если даны две стороны и один прилежащий угол.
Так как один из углов треугольника может быть тупым, значение синуса тупого угла находится по формуле приведения sin 180 ° − α = sin α .
Наиболее часто используемые тупые углы:
sin120 ° = sin 180 ° − 60 ° = sin60 ° = 3 2 ; sin150 ° = sin 180 ° − 30 ° = sin30 ° = 1 2 ; sin135 ° = sin 180 ° − 45 ° = sin45 ° = 2 2 .
Радиус описанной окружности
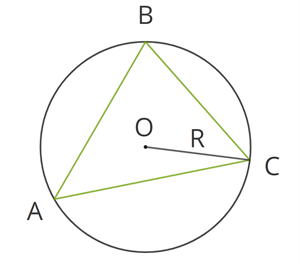
a sinA = b sinB = c sinC = 2 R , где \(R\) — радиус описанной окружности.
Выразив радиус, получаем R = a 2 sinA , или R = b 2 sinB , или R = c 2 sinC .
Теорема косинусов
Для вычисления элементов прямоугольного треугольника достаточно \(2\) данных величин (две стороны или сторона и угол).
Для вычисления элементов произвольного треугольника необходимо хотя бы \(3\) данных величины.
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
a 2 = b 2 + c 2 − 2 ⋅ b ⋅ c ⋅ cosA .
Также теорема исполняется для любой стороны треугольника:
b 2 = a 2 + c 2 − 2 ⋅ a ⋅ c ⋅ cosB ;
c 2 = a 2 + b 2 − 2 ⋅ a ⋅ b ⋅ cosC .
Теорема косинусов используется для вычисления:
неизвестной стороны треугольника, если даны две стороны и угол между ними;
вычисления косинуса неизвестного угла треугольника, если даны все стороны треугольника.
Значение косинуса тупого угла находится по формуле приведения cos 180 ° − α = − cos α .
Наиболее часто используемые тупые углы:
cos120 ° = cos 180 ° − 60 ° = − cos60 ° = − 1 2 ; cos150 ° = cos 180 ° − 30 ° = − cos30 ° = − 3 2 ; cos135 ° = cos 180 ° − 45 ° = − cos45 ° = − 2 2 .
Если необходимо найти приблизительное значение синуса или косинуса другого угла или вычислить угол по найденному синусу или косинусу, то используется таблица или калькулятор.
Определение знака
Достоверность результата зависит от правильного решения. Неверный знак функции способен кардинально его изменить. Для безошибочного определения значений потребуются еще кое-какие знания. К ним относятся следующие: понятие о системе координат и теорема Пифагора, а также умение чертить окружность с определенным радиусом.
Системы координат, которые применяются при решении задач бывают полярными и декартовыми. Последние используются чаще, чем первые. Полярные применяются для решения задач из области высшей математики, а также в других сложных дисциплинах с физико-математическим уклоном.
Дополнительные сведения
Для определения знака применяется обыкновенная система координат с двумя осями. Одна из них (ОХ) является осью абсцисс, а другая (ОУ) — ординат. Ее центром, который совпадает с центром тригонометрической окружности, является точка «О». Очень часто для работы необходимо знание теоремы Пифагора. Ее формулировка имеет следующий вид: в любом прямоугольном треугольнике выполняется равенство квадрата гипотенузы и суммы квадратов катетов. Вторая формулировка записывается в виде формулы: с^2 = a^2 + b^2 (c, a и b — гипотенуза и два катета соответственно).
Необходимо обратить внимание на следующий факт: сумма всех углов треугольника составляет 180 градусов, то есть является развернутым углом. Математически утверждение можно записать следующим образом через углы а, b и c: а + b + c = 180
Кроме того, существуют и другие соотношения между острыми углами прямоугольного треугольника: cos (a) = sin (b), cos (b) = sin (a), tg (a) = ctg (b), и tg (b) = ctg (a).
Чтобы найти знаки тангенса и котангенса по четвертям, используются такие соотношения: tg (a) = sin (a) / cos (a) и ctg (a) = cos (a) / sin (a).
Построение окружности
Сделать «инструмент», который значительно ускорит процесс решения задач довольно просто. Для этого нужно построить декартовую систему координат и единичную окружность с центром в точке О (точка пересечения осей абсцисс и ординат). Горизонтальная ось обозначается «х», а вертикальная — «у».
Рекомендуется чертить произвольную окружность. Чертеж должен быть простым и понятным. Это называется масштабирование, при котором изображение не соответствует действительному размеру объекта. Его примером является обыкновенная географическая карта. Кроме того, при проектировании очень мелких деталей применяются чертежи, которые в несколько десятков или сотен раз превышают натуральные размеры. Обозначение точки на плоскости выполняется следующим образом:
- Координаты заключаются в круглые скобки и разделяются «;».
- На первом месте стоит значение, соответствующее оси абсцисс, а на втором — ординат: (x;y).
Окружность пересекает оси в четырех точках: (1;0), (0;1), (-1;0) и (0;-1). Четвертями называются области, которые делят систему координат на четыре равные части. Отсчет выполняется от первой четверти (x>0 и y>0) против часовой стрелки:
- Значения по x и y больше 0 соответствуют первой четверти (I).
- II: x<0 и y>0.
- III: x<0 и y<0.
- IV: x>0 и y<0.
Ось ординат соответствует всем значениям sin углов альфа и бета, а абсцисс — всем cos. Следовательно, по тригонометрической окружности можно определить знаки косинуса и синуса по четвертям. Рекомендуется отметить для удобства значения углов в радианах рядом с точками пересечения следующим образом:
- 0 и 2ПИ (0 и 360 градусов) — (1;0).
- ПИ/2 (90) — (0;1).
- 3ПИ/2 (270) — (1;0).
Использование готового инструмента
Однако необязательно самостоятельно чертить единичную окружность для определения знаков. Можно воспользоваться уже готовыми вариантами (например, рис. 1).
Рисунок 1. Пример тригонометрического круга.
Косинус положителен в четвертях I и IV. Существуют области, где синус положителен: I и II. Функции tg и ctg положительны только в I и III четвертях. Однако перед тем, как приступить к решению задач, нужно понять термин «четность и нечетность функции». В тригонометрии они обладают такими свойствами:
- cos(-a) = cos(a).
- sin(-a) = -sin(a).
- tg(-a) = -tg(a).
- ctg(-a) = -ctg(a).
С помощью единичной окружности можно не только находить знаки функций, но и их значения. Например, для определения знака и значения cos(270) следует воспользоваться таким алгоритмом:
- Определить четверть, в которой находится угол: 240 = 4ПИ/3 соответствует III четверти.
- В III четверти величина функции принимает только отрицательные значения. Значит, перед ней следует поставить знак «минус».
- Вычислить: cos(4ПИ/3) = — 1/2.
Когда угол представлен отрицательным значением, то следует правильно раскрыть скобки. Например, sin(-4ПИ/3) = — (-1/2) = 1/2.
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Координата по оси x – косинус угла , координата по оси y – синус угла .
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .
Формулы сложения и вычитания углов
Перейдем к сложению и вычитанию аргумента. В записи задания это обычно выглядит, например, так: \(tg(\alpha+\beta)\) или \(ctg(\alpha-\beta)\). Если повезет, выражение в аргументе может прийти к обычному углу, который достаточно легко посчитать. Однако, не всегда все так просто.
Например, попробуем посчитать \(sin(45+60)\). В скобках получаем угол в 105 градусов, что не является табличным значением. Что же делать? Считать через аркфункцию? Подробнее про аркфункцию мы поговорим чуть дальше.
На самом деле, мы можем воспользоваться формулами сложения и вычитания углов. Рассмотрим их.
\(sin(\alpha\pm\beta)=sin\alpha*cos\beta \pm cos \alpha*sin\beta\) \(cos(\alpha\pm\beta)=cos \alpha*cos\beta \mp sin \alpha*sin\beta\)\(tg(\alpha\pm\beta)=\frac{tg \alpha \pm tg\beta}{ 1\pm tg \alpha*tg\beta}\)\(ctg(\alpha\pm\beta)=\frac{ctg \alpha*ctg\beta\mp1}{ctg\beta\mp ctg\beta \pm \alpha}\)
Заметим, что в этих формулах у нас появился знак \(\mp\). Знаки \(\pm\) и \(\mp\) отличаются друг от друга и эту разницу мы сейчас обсудим.
Знак \(\mp\) означает, что нам нужно использовать противоположный знак тому, который стоит в аргументе. Например, у нас в аргументе стоит +, тогда при преобразовании формулы мы должны поменять его на минус. Например, \(cos(a+\beta)=cos a*cos\beta -sin a*sin\beta\).Точно так же с этим знаком минус меняется на плюс.
Если в аргументе стоит привычный \(\pm\), то знаки мы не меняем и используем те же, что даны изначально. Например, \(sin(a+\beta)=sin a*cos \beta+cos a*sin \beta\).
Чтобы точно не запутаться в преобразовании знаков, нужно ориентироваться по одной стороне. Например, если в примере у нас стоит знак сверху, то и все остальные знаки для преобразований мы берем сверху.
Рассмотрим \(tg(a-\beta)\). Заметим, что в изначальной формуле минус стоит снизу, значит, для преобразований берем только нижние знаки. Получаем:
\(tg(a-\beta)=\frac{tg a-tg\beta}{1+tg a*tg \beta}\)
Теперь попробуем решить наше выражение sin(45+60). Применим формулу и получим:
\(sin(45+60)=sin 45*cos 60+cos 45*sin 60\)
Далее нам просто нужно подставить табличные значения синусов и косинусов. Саму таблицу мы приложили ниже, а подробнее про работу с ней рассказывали в статье «Тригонометрическая окружность. Часть 1».
По таблице получаем:
\(sin 45*cos 60+cos 45*sin 60=\frac{\sqrt2}{2}*\frac{1}{2}+\frac{\sqrt2}{2}*\frac{\sqrt3}{2}\)
Осталось посчитать выражение и найти ответ:
\(\frac{\sqrt2}{2}*\frac{1}{2}+\frac{\sqrt2}{2}*\frac{\sqrt3}{2}=\frac{\sqrt2}{4}+\frac{\sqrt6}{4}=\frac{\sqrt2+\sqrt6}{4}\)
Аргументы мы меняли различными способами. Можем ли как-то поменять саму тригонометрическую функцию? Конечно! Например, возведем ее в квадрат.
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается
Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается
Угол обозначается соответствующей греческой буквой .
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
- С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла катет а будет прилежащим.Получаем, что . Иными словами, .
- Возьмем теорему Пифагора: . Поделим обе части на : Мы получили основное тригонометрическое тождество.
- Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .
| − |
| − |
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
1. В треугольнике угол равен , . Найдите .
Задача решается за четыре секунды.
2 . В треугольнике угол равен , , . Найдите .
Найдем по теореме Пифагора.
Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!
Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Группа 2: основные тождества
Первое и самое главное тождество — теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. Применительно к треугольнику , рассмотренному выше, эту теорему можно записать так:
И сразу — небольшое замечание, которое убережет читателя от множества ошибок. Когда решаете задачу, всегда (слышите, всегда!) записывайте теорему Пифагора именно в таком виде. Не пытайтесь сразу выражать катет, как это обычно требуется. Возможно, вы сэкономите пару строчек вычислений, но именно на этой «экономии» было потеряно больше баллов, чем где-либо еще в геометрии.
Второе тождество — из тригонометрии. Выглядит следующим образом:
Оно так и называется: основное тригонометрическое тождество. С его помощью можно через синус выразить косинус и наоборот.
Определения функций и их связь
Вернемся к единичной окружности в прямоугольной системе координат, где центр окружности и системы координат совпадает. Точку А(1,0) повернём на 90°, и из полученной точки А1 проведём перпендикуляр к абсциссе. В результате получится прямоугольный треугольник, где угол А1 ОН это угол поворота а. длины катета ОН и абсциссы точки А1 также равны. А катет, который находится напротив угла равен ординате точки А1, а длина гипотенузу это единица.
Получается исходя из определения, синус угла а, это отношение катета напротив к гипотенузе.
sin α = A 1 H\ O A 1 = y \1 = y
sin α=A1H\OA1=y\1=y
Из чего следует, что определение sin острого угла, одинаково определению синуса угла поворота а, если а лежит в пределе 0-90°. Точно так же и с вычислением косинуса, тангенса и котангенса.
Примеры решения задач
А теперь попробуем с помощью полученных знаний решить наиболее распространенные задачи B8. Не удивляйтесь, что с таким арсеналом текст решения окажется не намного длиннее, чем исходное условие. И это радует ![]()
По определению (группа 1), cos = : . Гипотенуза нам известна, а вот катет придется искать. Обозначим его = .
Переходим к группе 2. Треугольник — прямоугольный. По теореме Пифагора:
Теперь можно найти косинус:
Обозначим искомую сторону = и рассмотрим треугольник . Он прямоугольный, причем ∠ = 90° по условию. Поэтому cos = : = : = 4/5. Это пропорция, ее можно переписать так: 5 · = 4 · . Очевидно, мы найдем , если будем знать .
Рассмотрим треугольник . Он также прямоугольный, причем cos = : . Ни , ни нам не известны, поэтому переходим ко второй группе фактов. Запишем основное тригонометрическое тождество:
Поскольку тригонометрические функции острого угла положительны, получаем sin = 3/5. С другой стороны, sin = : = 3 : . Получаем пропорцию:
Итак, = 5. Тогда = · cos = 5 · 4/5 = 4. Наконец, находим = :
Обозначим искомую высоту = . Перед нами равнобедренный треугольник , в котором = . Следовательно, из третьей группы фактов имеем:
Рассмотрим треугольник . Он прямоугольный (∠ = 90°), причем = 5 и cos = 0,8. По определению, cos = : = : 5. Получаем пропорцию:
Осталось воспользоваться второй группой фактов, а именно теоремой Пифагора для треугольника :
Поскольку нам известна гипотенуза = 40 и катет = 32, можно найти косинус угла : cos = : = 32 : 40 = 0,8. Это был факт из первой группы.
Зная косинус, можно найти синус через основное тригонометрическое тождество (факт из второй группы):
При нахождении синуса вновь был использован тот факт, что тригонометрические функции острого угла положительны. Осталось заметить, что углы и смежные. Из первой группы фактов имеем:
Треугольник — равнобедренный, — высота, поэтому заметим, что = = 0,5 · = 0,5 · 8 = 4. Это факт из третьей группы.
Теперь рассмотрим треугольник : в нем ∠ = 90°. Можно выразить тангенс: tg = : . Но = 4, поэтому остается найти сторону , которую обозначим = . По теореме Пифагора (факт из группы 2) имеем:
Теперь все готово, чтобы найти тангенс: tg = : = 3 : 4 = 0,75.
Обозначим искомую высоту = . Снова треугольник — равнобедренный, поэтому заметим, что ∠ = ∠, следовательно, cos = cos = 3/5. Это факт из третьей группы.
Рассмотрим треугольник . По условию, он прямоугольный (∠ = 90°), причем известна гипотенуза = 6 и cos = 3/5. Но cos = : = : 6 = 3/5. Получили пропорцию:
Теперь найдем = по теореме Пифагора для треугольника :
Общая схема решения задачи B8
Геометрия отличается от алгебры тем, что в ней нет простых и универсальных алгоритмов. Каждую задачу приходится решать с нуля — и в этом ее сложность. Тем не менее, общие рекомендации дать все-таки можно.
Для начала, следует обозначить неизвестную сторону (если таковая имеется) за . Затем применяем схему решения, которая состоит из трех пунктов:
- Если в задаче есть равнобедренный треугольник, применить к нему все возможные факты из третьей группы. Найдите равные углы и выразите их тригонометрические функции. Кроме того, равнобедренный треугольник редко бывает прямоугольным. Поэтому ищите в задаче прямоугольные треугольники — они там обязательно есть.
- Применить к прямоугольному треугольнику факты из первой группы. Конечная цель — получить уравнение относительно переменной . Найдем — решим задачу.
- Если фактов из первой группы оказалось недостаточно, применяем факты из второй группы. И снова ищем .






