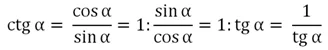Тангенс

Способ 1 – вычисление тангенсов и котангенсов через синусы и косинусы

Конечно, этот способ подразумевает, что вы уже умеете вычислять синус и косинус. Не умеете? Тогда бегом читать эту статью, и эту тоже.

Уже умеете? Тогда ловите два определения:

– тангенс равен отношению синуса к косинусу числа.

(tg ,t=)(frac{sin⁡,t}{cos,⁡t})

– котангенс равен отношению косинуса к синусу числа.

(ctg ,t=)(frac{cos⁡,t}{sin,⁡t})

Пример. Вычислите (tg, frac{π}{3}) и (ctg, frac{π}{3}).Решение:

Ищем сначала (frac{π}{3}), а после вычисляем (sin,⁡frac{π}{3}) и (cos⁡,frac{π}{3}).

(sin⁡, frac{π}{3}=frac{sqrt{3}}{2});      (cos⁡, frac{π}{3}=frac{1}{2});
(tg , frac{π}{3}=) (frac{frac{sqrt{3}}{2}}{frac{1}{2}})(=frac{sqrt{3}}{2}:frac{1}{2}=frac{sqrt{3}}{2}cdot frac{2}{1}=sqrt{3}).
(ctg,frac{π}{3}=)(frac{frac{1}{2}}{frac{sqrt{3}}{2}})(=frac{1}{2}:frac{sqrt{3}}{2}=frac{1}{2}cdotfrac{2}{sqrt{3}}=frac{1}{sqrt{3}}).

Пример. Вычислите (tg, frac{5π}{6}) и (ctg, frac{5π}{6}).Решение:

Найдем сначала (frac{5π}{6}) на круге: (frac{5π}{6}=frac{6π}{6}-frac{π}{6}=π-frac{π}{6}).

(ctg, frac{5π}{6}=)(frac{cos⁡ frac{5π}{6}}{sin⁡frac{5π}{6}})(=-frac{sqrt{3}}{2}:frac{1}{2}=-frac{sqrt{3}}{2} cdot frac{2}{1}=-sqrt{3});
(tg,frac{5π}{6}=)(frac{sin⁡frac{5π}{6}}{cos⁡frac{5π}{6}})(=frac{1}{2}:(-frac{sqrt{3}}{2})=frac{1}{2}cdot(-frac{2}{sqrt{3}})=-frac{1}{sqrt{3}}).

Пример. Вычислите (tg, 0) и (ctg, 0).Решение:

(0) на тригонометрическом круге совпадает с (1) на оси косинусов, значит (cos⁡,0=1).
Если из точки (0) на тригонометрическом круге провести перпендикуляр (красная пунктирная линия) к оси синусов, то мы попадем в (0), получается (sin,⁡0=0). Следовательно: (tg, 0=)(frac{sin,⁡0}{cos⁡,0}) (=frac{0}{1}=0).

С котангенсом интереснее: (ctg, 0=)(frac{cos,⁡0}{sin⁡,0}) (=frac{1}{0}=???). На ноль делить нельзя – это железное правило математики. Поэтому и посчитать такой котангенс не получится. (ctg,⁡0) – не вычислим в принципе.

Пример. Вычислите (tg,120^°) и (ctg, 120^°).Решение:

(ctg,120^°=)(frac{cos⁡,120^°}{sin,120^°})(=-frac{1}{2}:frac{sqrt{3}}{2}=-frac{1}{2}cdotfrac{2}{sqrt{3}}=-frac{1}{sqrt{3}});
(tg,120^°=)(frac{sin⁡,120^° }{cos⁡,120^°})(=frac{sqrt{3}}{2}:(-frac{1}{2})=frac{sqrt{3}}{2}cdot(-frac{2}{1})=-sqrt{3}).

Основные тригонометрические функции

Пусть есть некоторый прямоугольный треугольник АBС, у которого∠С = 90°. Обозначим какой-нибудь его острый угол, например, ∠А, греческой буквой α. В треугольнике есть два катета. Тот из них, который, непосредственно является одной из сторон угла α, называют прилежащим катетом. Другой катет именуют противолежащим. Ещё одна сторона треугольника – это гипотенуза, для которой не надо уточнять, прилежащая она или противолежащая относительно острого угла:

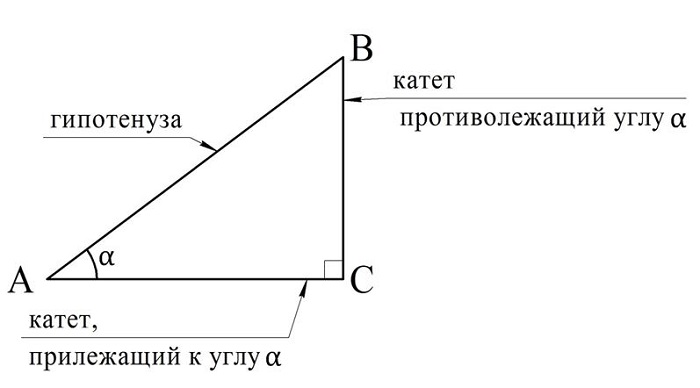
Отношения этих трех сторон друг к другу имеют особое наименование.

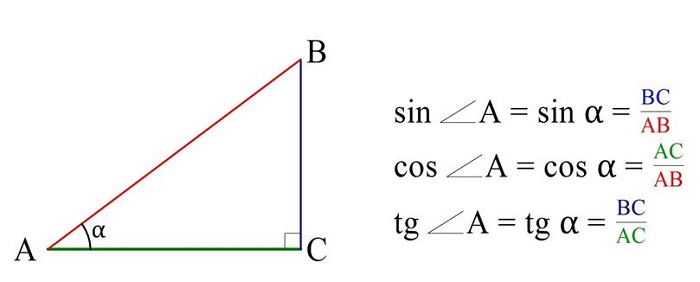
Для обозначения этих трех величин (их именуют тригонометрическими функциями) используют сокращения sin, cos и tg. При этом после этого сокращения может писаться как обозначение угла греческой буквой, так и обычное обозначение с помощью больших латинских букв:

Задание. Найдите значения тригонометрических функций для∠А в ∆АBС, длины сторон которого указаны на рисунке:

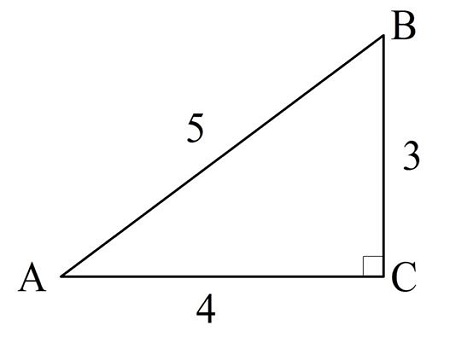
Решение. Просто пользуемся определениями каждой функции:

Задание. Найдите величину тригонометрических функций угла∠В в ∆АBС, показанном на рисунке:

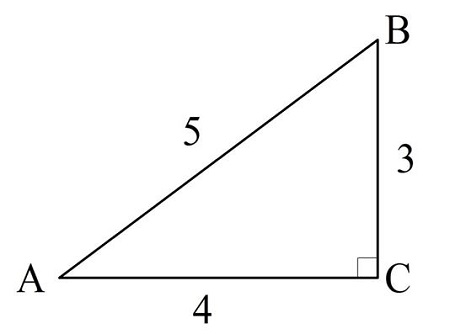
Решение. На первый взгляд кажется, что задание повторяет предыдущее, но это не так. В данном случае нам надо вычислять функции не для∠А, а для ∠В. Для него противолежащим катетом уже будет АС, а прилежащим – ВС. Тогда можно записать, что

Задание. В прямоугольном ∆АBС гипотенуза АB имеет длину 10, а sin∠A = 0,2. Найдите величину ВС.

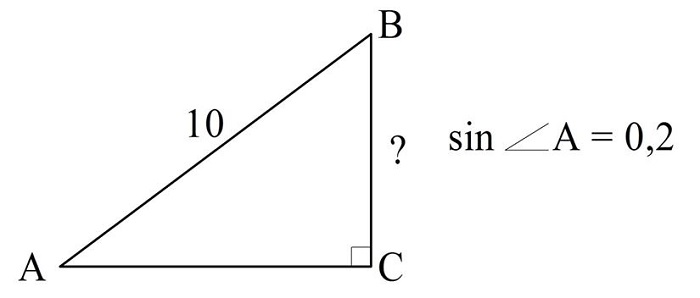
Решение. Запишем синус как отношение двух сторон:

Задание. В прямоугольном ∆АBС АС = 8, cos∠A = 0,4. Какова длина гипотенузы АB?

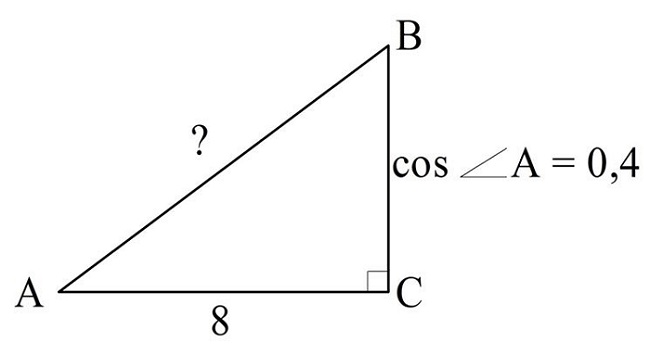
Решение. Выразим известный нам косинус как отношение двух отрезков:

Принципиально важно то, что если в двух прямоугольных треугольниках острые углы одинаковы, то и значение их синусов, косинусов и тангенсов также будут одинаковы. Действительно, пусть у ∆АBС и ∆А1В1С1 одинаковы∠А и ∠А1, а ∠С и ∠С1 – прямые:

Тогда у них совпадает по два угла, а это означает, что ∆АBС и ∆А₁В₁С₁ подобны. Из этого подобия вытекает пропорция:

Отсюда можно сделать вывод:

Другими словами, значение тригонометрической функции угла зависит только от величины угла (его градусной меры) и НЕ зависит от того, в каком прямоугольном треугольнике этот угол построен. Действительно, с помощью калькулятора или компьютера можно всегда посчитать синус для какого-то угла, если известна его величина в градусах.

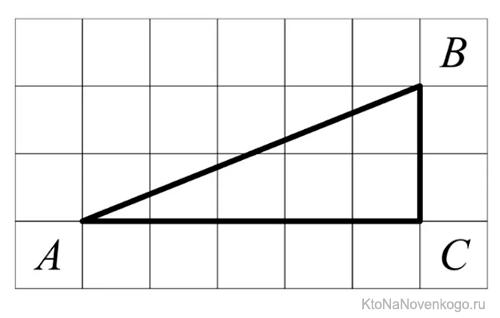
Задание. Найдите тангенс угла, изображенного на рисунке:

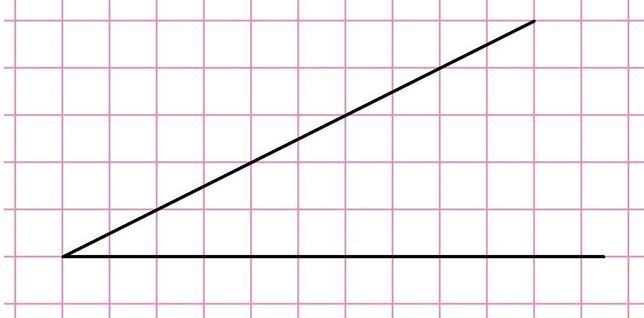
Решение. Нам надо самостоятельно достроить угол до прямоугольного треугольника. Удобней всего просто построить вертикальную линию, длину которой будет удобно измерить с помощью клеточек. Например, можно сделать такое построение:

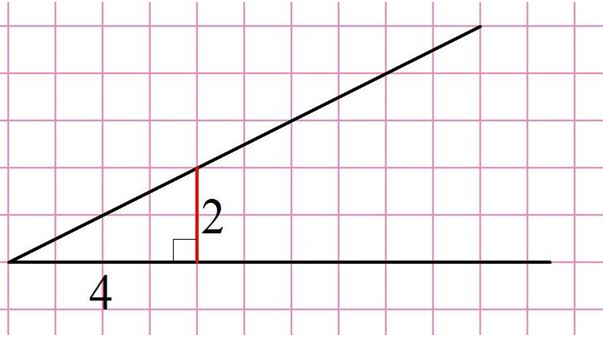
Тогда тангенс можно получить, поделив вертикальный отрезок (он здесь оказывается противолежащим катетом) на горизонтальный:

Заметим, что мы могли построить и треугольник с другими размерами, однако во всех случаях величина тангенса будет одной и той же:

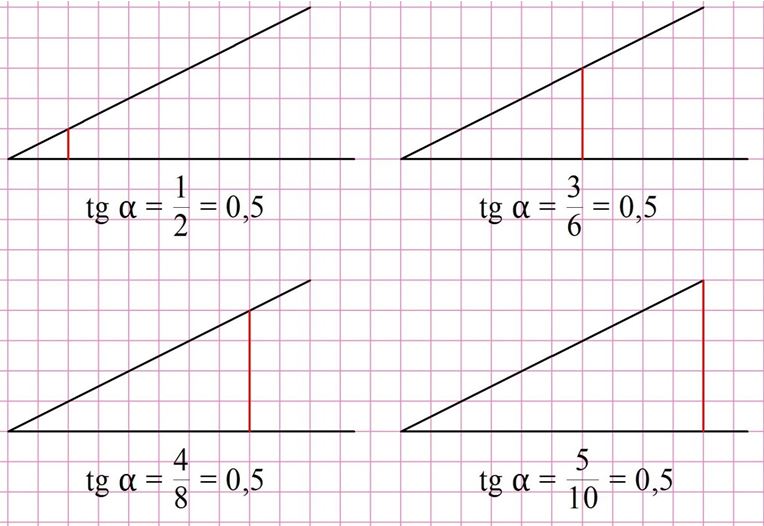
Ответ: 0,5

Задание. Постройте такой угол, что его тангенс будет равен 1,5.

Решение. Если тангенс равен 1,5, то это означает, что противолежащий катет в 1,5 раза длиннее прилежащего катета треугольника. В 1,5 раза отличаются, например, числа 2 и 3. Значит, если мы построим треугольник с катетами 2 и 3, то мы получим необходимый нам угол:

Понятие отрицательного тангенса

Тангенс отрицательный, когда противоположная сторона треугольника лежит в одной из следующих четырех частей плоскости:

• В третьем квадранте (секторе), где значения координат x и y отрицательные;
• В четвертом квадранте (секторе), где значение координаты x положительное, а значение координаты y отрицательное;
• Во втором квадранте (секторе), где значения координат x и y положительные;
• В первом квадранте (секторе), где значение координаты x отрицательное, а значение координаты y положительное.

Примеры отрицательного тангенса:

• Если противоположная сторона треугольника равна -3, а прилежащая сторона равна 1, то тангенс будет равен -3.
• Если противоположная сторона треугольника равна 4, а прилежащая сторона равна -2, то тангенс будет равен -2.

Отрицательный тангенс может быть важен при решении проблем в физике, инженерии и других науках, где углы и треугольники играют важную роль.

Тригонометрические функции стандартных углов

Итак, мы выяснили, что тригонометрические функции зависят от градусной меры угла. Попытаемся вычислить их для некоторых стандартных значений.

Начнем с угла в 30°. Построим прямоугольный ∆АBС с∠А = 30°:

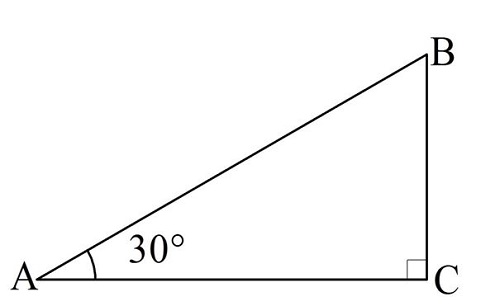
Ещё из 7-ого класса нам известно, что в таком треугольнике гипотенуза вдвое длиннее, чем катет, лежащий напротив угла в 30°:

Далее можно найти и тангенс 30°:

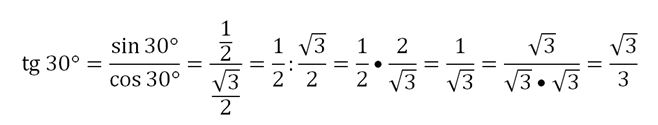
Вернемся к рассматриваемому нами ∆АBС, в котором∠А = 30°. Ясно, что другой его острый угол, ∠В, будет составлять 90 – 30 = 60°:

Снова используем тот факт, что гипотенуза АB будет длиннее катета ВС в 2 раза:

Ещё один стандартный угол, для которого легко можно рассчитать значение его тригонометрических функций – это 45°. Рассмотрим прямоугольный ∆АBС, в котором один из острых углов составляет 45°. Тогда и другой острый угол должен также составлять 45°, ведь их сумма в прямоугольном треугольнике равна 90°:

Но если в треугольнике 2 угла одинаковы, то он – равнобедренный, то есть катеты АС и ВС равны:

Итак, в результате нам удалось получить 9 стандартных значений, которые можно представить в виде единой таблицы тригонометрических функций:

Задание. Составьте формулу для вычисления площади прямоугольного треугольника, если известен один из его катетов (он равен a) и острый угол, прилегающий к этому катету (он обозначается как α). Далее найдите c помощью формулы площадь треугольника, если а = 5 и α = 45°.

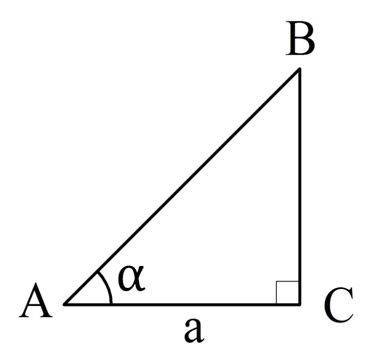
Решение. Как известно, площадь прямоугольного треугольника рассчитывается по формуле:

Задание. В прямоугольном ∆АBС к гипотенузе ВС проведена высота АН. Отрезок НВ имеет длину 16. Известно, что sinα = 0,6. Какова длина СН?

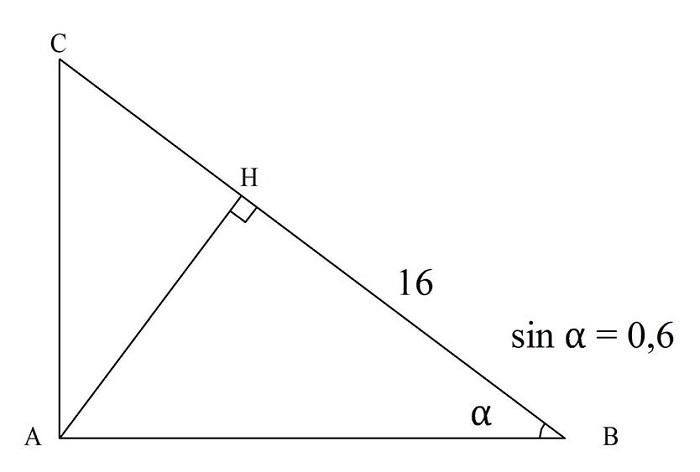
Решение. Сначала, зная sinα, найдем сosα и tgα:

Теперь заметим, что на рисунке угол α – это не только ∠АBС. Действительно, в ∆АBС

Нам известен отрезок АН и tg∠САН, поэтому можно найти СН:

Расположение точек во второй четверти числовой окружности

Во второй четверти числовой окружности находятся точки, у которых значения тригонометрических функций тангенса и котангенса отрицательны.

Чтобы понять, почему это так, рассмотрим определение этих функций. Тангенс угла в тригонометрии — это отношение противоположного катета к прилежащему катету в прямоугольном треугольнике. Если мы рассматриваем угол, лежащий во второй четверти, то противоположный и прилежащий катеты будут иметь отрицательные значения. Поэтому результат операции «противоположный катет / прилежащий катет» будет также отрицательным числом.

Аналогично, котангенс угла — это отношение прилежащего катета к противоположному катету в прямоугольном треугольнике. Во второй четверти значения обоих катетов будут отрицательными, поэтому результат операции «прилежащий катет / противоположный катет» также будет отрицательным числом.

Для более понятного объяснения рассмотрим пример. Предположим, у нас есть угол во второй четверти числовой окружности с координатами (x, y), где x и y — отрицательные числа. Если мы построим прямоугольный треугольник с катетами, равными x и y, то можно заметить, что значения тангенса и котангенса этого угла будут отрицательными числами. Это объясняется расположением точек во второй четверти числовой окружности.

Как найти значения сторон постоянного треугольника

Постоянным треугольником называют равнобедренный треугольник, у которого две стороны одинаковой длины. В таком треугольнике основание (основная сторона), соединяющее вершины с разными углами, будет самой короткой стороной, а две равные стороны, выполняющие функцию боковых сторон, будут длиннее.

Для нахождения значений сторон постоянного треугольника можно использовать следующие подходы:

1. Использовать формулу тангенса угла и известное значение одной из сторон треугольника.
2. Использовать формулу для нахождения длины основания по известным значениям боковых сторон.

Важно помнить, что в постоянном треугольнике, две боковые стороны равны между собой, поэтому для нахождения значения одной из них, можно использовать известное значение другой боковой стороны. Для нахождения значений сторон постоянного треугольника можно использовать таблицу соотношений сторон и углов, которая позволит с легкостью определить длины сторон треугольника в зависимости от известных значений:

Для нахождения значений сторон постоянного треугольника можно использовать таблицу соотношений сторон и углов, которая позволит с легкостью определить длины сторон треугольника в зависимости от известных значений:

Боковая сторона	Основание	Угол	Формула
a	b	α	a = b * sin(α)
β	a = b * cos(β)
a	b	γ	b = a / sin(γ)
β	b = a * tan(β)
b	a	γ	a = b * sin(γ)
α	a = b / tan(α)

Таким образом, для нахождения значений сторон постоянного треугольника можно использовать формулы для тригонометрических функций (синус, косинус, тангенс) углов треугольника, а также таблицу соотношений сторон и углов. Это позволит определить длины сторон треугольника в зависимости от известных значений и сделать необходимые расчеты.

Почему важно знать тангенс угла в треугольнике?

Знание тангенса угла в треугольнике имеет несколько важных применений:

1. Решение геометрических задач. Треугольники имеют широкое применение в геометрии, и знание тангенса угла позволяет находить различные величины их сторон и углов. Это особенно полезно при решении задач на построение или нахождение неизвестных параметров треугольников.
2. Работа с физическими задачами. Многие физические явления и законы можно описать с помощью треугольников и их углов. Знание тангенса угла позволяет решать задачи на определение силы давления, силы трения, углового ускорения и других физических величин.
3. Построение графиков и анализ данных. В математике и науке широко используется построение графиков функций. Знание тангенса угла позволяет анализировать данные и строить соответствующие графики. Он также может быть использован при решении задач на определение углов наклона или сцепления в графиках и изображениях.
4. Разработка компьютерной графики и анимации. В компьютерной графике и анимации треугольники широко используются для построения и описания геометрических форм. Тангенс угла играет важную роль при расчете координат точек, задания перспективы, вращении и трансформации объектов.

Важно осознавать, что понимание тангенса угла способствует расширению знаний в математике, физике, компьютерных науках и других областях. Это позволяет более эффективно решать задачи и выполнять прикладные задания, а также стимулирует развитие логического мышления и умения анализировать данные

Что такое тангенс угла и как его найти

Живущим людям на Землевсегда хотелось знать,как путь найти в пустыне, море,и можно к звёздам ли попасть.

Хотелось труд свой облегчить,создать машины, чтоб летать.И чтоб вопросы разрешить,пришлось про тангенс всем узнать.

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Впервые встречаясь с тригонометрией в восьмом классе на геометрии, школьники оглядываются на свою жизнь, задавая вопрос, насколько пригодится им эта область науки в дальнейшем.

Редко кто задумывается, что раздел математики, позволяющий рассказать о заданном треугольнике всё (найти все его стороны и углы, выделить особенности), позволил в своё время сделать великие открытия.

Тригонометрия, дав возможность строить корабли и самолёты, отправлять человека в космос, создавать приборы для ориентирования на море, в лесу, в пустыне, определять расстояния, не измеряя их непосредственно линейкой, шагами или чем-то иным, помогла упростить жизнь человечества, раскрыть новые горизонты знаний.

Определение тангенса угла прямоугольного треугольника

Для этого строится нужный треугольник заданным углом, который необходимо определить.

Строится угол, точка и луч, которые выходят из данной точки под определенным углом. Соединяем лучи, прямой линией перпендикулярной, одному из лучей. В конечном итоге получаем фигуру, угол которой равняется заданному в задаче углу. В процессе вычисления, также задаются длины сторон. Поэтому трудней с построением не должно возникнуть.

Вычисление при помощи длин сторон треугольника происходит следующим образом:

• обозначается катет;
• сторона возле угла;
• сторона напротив угла с прямым значением.

Функции могут выражаться по-разному в отношении сторон.

Как найти значение синуса и косинуса угла?

Синус и косинус являются тригонометрическими функциями, которые позволяют вычислить значения углов в треугольнике. Эти функции широко используются в математике, физике, инженерии и других науках.

Для вычисления синуса и косинуса угла существуют несколько способов. Рассмотрим два основных метода:

1. По формуле тригонометрических функций:

• Для вычисления синуса угла нам необходимо разделить противолежащую сторону треугольника на гипотенузу.
• Для вычисления косинуса угла нам необходимо разделить прилежащую к углу сторону треугольника на гипотенузу.

С использованием таблиц и графиков тригонометрических функций:

• Для нахождения синуса и косинуса угла по таблице необходимо найти значение угла в таблице и считать соответствующие значения синуса и косинуса.
• Если таблицы нет, можно использовать график тригонометрических функций и отобразить на нем значения угла и соответствующие значения синуса и косинуса.

Пример:

Допустим, у нас есть треугольник ABC, где угол А равен 45 градусов, сторона AB равна 5 единиц, а сторона AC равна 7 единиц.

1. По формуле тригонометрических функций:

• Для синуса угла А: sin(45) = 5/7 = 0,714
• Для косинуса угла А: cos(45) = 5/7 = 0,714

2. С использованием таблицы:

В таблице найдем значение угла 45 градусов и найдем соответствующие значения синуса и косинуса:

Угол (градусы)	Синус	Косинус
45	0,707	0,707

Таким образом, значение синуса и косинуса угла 45 градусов равны 0,707.

Стандартные углы

Итак, значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $ и $\operatorname{ctg}\alpha $ однозначно определяются величиной угла $\alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.

Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:

1. Для большинства углов $\alpha $ нельзя найти точные значения $\sin \alpha $, $\cos \alpha $, $\operatorname{tg}\alpha $.
2. Верно и обратное: для большинства «красивых» $\sin \alpha $, $\cos \alpha $ и т.д. нельзя подобрать подходящий угол $\alpha $.

Звучит немного непонятно, поэтому разберём каждый пункт на конкретных примерах.

3.1. Три стандартных угла

Существует лишь три острых угла, для которых легко считаются синусы, косинусы и т.д. Это 30°, 45°, 60°. Вот их синусы, косинусы и тангенсы:

\

Чтобы понять, чем эти углы такие особенные, просто посчитаем все эти синусы, косинусы и тангенсы. Начнём с $\alpha =45{}^\circ $. Для этого рассмотрим равнобедренный прямоугольный треугольник. Мы уже встречались с ним:

Поскольку в равнобедренном треугольнике $\angle A=\angle B=45{}^\circ $, получим:

\

Это именно те значения, которые указаны в таблице!

Теперь разберёмся с углами $\alpha =30{}^\circ $ и $\alpha =60{}^\circ $. Здесь рассуждения будут чуть сложнее. Сначала рассмотрим равносторонний треугольник $ABC$ со стороной $AB=2$ (просто так удобнее) и проведём высоту $BH$:

Мы знаем, что высота $BH$ — ещё и медиана, и биссектриса. Поэтому $AH=CH=1$, $\angle ABH=\angle CBH=30{}^\circ $.

Следовательно, треугольник $ABH$ — прямоугольный, да ещё и с острыми углами 30° и 60°. По теореме Пифагора легко найти $BH=\sqrt{3}$. Нанесём все данные на чертёж:

Разберёмся с углом 60°:

\

И с углом 30°:

\

Попробуйте повторить все эти рассуждения самостоятельно. Это очень полезное упражнение!

Возникает вопрос: как быть с другими углами? Например, можно ли найти $\sin {50}^\circ $? Или, быть может, $\cos {10}^\circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.

Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?

3.2. Что с другими углами?

Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:

Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $\alpha $:

\

Итак, мы знаем синус

Внимание, вопрос: каким должен быть угол $\alpha $, чтобы $\sin \alpha =0,6$? Сколько градусов должно быть в угле $\alpha $? Ответ: неизвестно.:). Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$

Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует

Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $\alpha $, чтобы $\sin \alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.

Из всех этих рассуждений сделаем важный вывод. В тригонометрии мы:

• Либо берём угол и считаем для него синусы, косинусы и т.д. Но лишь для трёх острых углов — 30°, 45°, 60° — всё будет считаться быстро и красиво. Такие углы называются табличными.
• Либо берём синус, косинус или тангенс и для него пытаемся подобрать острый угол. Но лишь для табличных значений мы сможем подобрать такие углы. И да: это будут углы 30°, 45°, 60°.

Ещё раз:

И наоборот:

С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.

Тригонометрия простыми словами

Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».

Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:

• Синус угла – отношение противолежащего катета к гипотенузе;
• Косинус угла – отношение прилежащего катета к гипотенузе;
• Тангенс угла – отношение противолежащего катета к прилежащему;
• Котангенс угла – отношение прилежащего катета к противолежащему.

Или в виде формул:

Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).

Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.

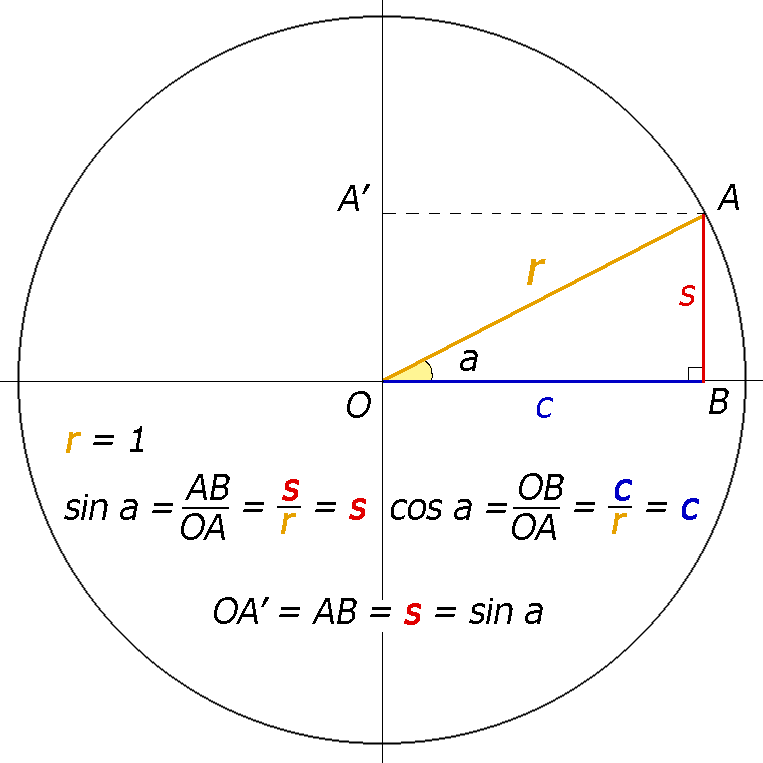
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.

Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.

Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.

Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.

Свойства тангенса

Ниже в табличной форме представлены основные свойства касательной с формулами.

Свойство	Формула
Симметрия	tg (-α) = -tg α»порядок данных=»tg (-α) = -tg α»>tg (-α) = -tgα
Симметрия	tg (90°- α) = ctg α»data-order=»tg (90°- α) = ctg α»>tg (90°- α) = ctg α
Тригонометрические тождества	загар α = грех α / потому что α» data-order=»tg α = sin α / cos α»>tg α = sin α / cos α
	tg α = 1 / ctg α «данные-порядок=»tg α = 1 / ctg α»>tg α = 1 / ctg α
Тангенс двойного угла	tg 2α = 2 tg α / (1 — tg2 α)» data-order=»tg 2α = 2 tg α / (1 — tg2 α)»>tg2α = 2tgα / (1 — tg2α)
Тангенс суммы углов	tg (α+β) = (tg α + tg β) / (1 — tg α tg β)» data-order=»tg (α+β) = (tg α + tg β) / (1 — tg α tg β)»>tg (α+β) = (tg α + tg β) / (1 — tg α tg β)
Тангенс разности углов	tg (α-β) = (tg α — tg β) / (1 + tg α tg β)» data-order=»tg (α-β) = (tg α — tg β) / (1 + tg α tg β)»>tg (α-β) = (tg α — tg β) / (1 + tg α tg β)
Сумма тангенсов	tg α + tg β = sin (α + β) / cos α cos β» data-order=»tg α + tg β = sin (α + β) / cos α cos β»>tg α + tg β = sin (α + β) / cos α cos β
Тангенс разница	tg α — tg β = sin (α — β) / cos α cos β» data-order=»tg α — tg β = sin (α — β) / cos α cos β»>tg α — tg β = sin (α — β) / cos α cos β
Произведение касательных	tg α tg β = (tg α + tg β) / (ctg α + ctg β)» data-order=»tg α tg β = (tg α + tg β) / (ctg α + ctg β)»>tg α tg β = (tg α + tg β) / (ctg α + ctg β)
Произведение тангенса и котангенса	tg α ctg β = (tg α + ctg β) / (ctg α + tg β)» data-order=»tg α ctg β = (tg α + ctg β) / (ctg α + tg β)»>tg α ctg β = (tg α + ctg β) / (ctg α + tg β)
Касательная производная	tg’ x = 1 / cos2 (x)» порядок данных=»tg’ x = 1 / cos2 (x)»>tg’ х = 1 / cos2 (х)
Касательный интеграл	∫ тангенс x dx = -ln |cos x| +C»заказ данных=»∫ tg x dx = -ln |cos x| + C»>∫ тангенс х dx = -ln | cos х | + C
Формула Эйлера	tg x = (eix — e-ix) / i(eix + e-ix)» data-order=»tg x = (eix — e-ix) / i(eix + e-ix)»>tg x = (eix — e-ix) / i(eix + e-ix)

Примеры применения Tan в инженерии и науке

Функция тангенса (tan) имеет широкое применение в различных областях науки, включая физику, инженерию и геометрию. Вот несколько примеров ее использования:

• Электрические цепи: tan может использоваться для определения фазовых углов в электрических цепях, что позволяет инженерам лучше понимать и проектировать электрические системы.
• Архитектура: tan используется для определения углов наклона крыш, наклонов стен и других деталей зданий.
• Физика: tan используется для расчета углов наклона материалов, благодаря чему ученые могут определить, как различные материалы будут вести себя при различных условиях.
• Навигация: в навигации тангенс используется для определения расстояний между телами и углах между различными направлениями.
• Строительство: tan используется для вычисления углов в строительстве, чтобы строительные конструкции были устойчивыми.

Каждый пример применения tan показывает, как эта функция является неотъемлемой частью инженерии и науки. Знание тангенса и его применений позволяет ученым и инженерам определить углы, расстояния и другие параметры, необходимые для успешного проектирования и постройки различных систем и конструкций.

Котангенс угла

Помимо тангенса в тригонометрии выделяют ещё одну производную ф-цию – котангенс. Он представляет отношение косинуса к синусу:

Видно, что определение котангенса очень похоже определение тангенса. В принципе, удобней использовать несколько другую формулу:

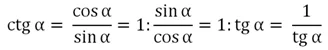
Почти во всех задачах с помощью формулы

можно избавиться от котангенса, заменив его дробью 1/tgα. Поэтому мы вкратце расскажем об основных особенностях котангенса, ведь он очень редко используется на практике.

Значения этой ф-ции рассчитываются так:

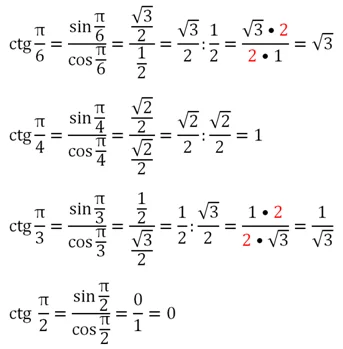
При х = 0 значение котангенса не определено, так как в этой точке косинус становится равным нулю, а деление на ноль невозможно.

График котангенса – это тангенсоида, которая отображена симметрично относительно оси Ох и смещена на π/2:

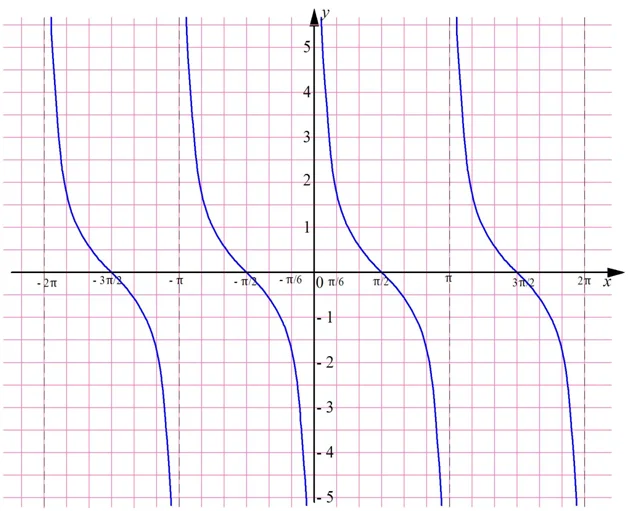
Можно заметить, что вертикальные штриховые линии (асимптоты) графика проходят через точки, кратные π: –2π, – π, 0, π, 2π… Они разбивают координатную прямую на интервалы (– 2π; – π), (– π; 0), (0; π), (π; 2π), на каждом из которых ф-ция у = ctgx убывает. Видно, что котангенс – это периодическая ф-ция с периодом π.

Для сравнения покажем на одной плоскости графики тангенса и котангенса:

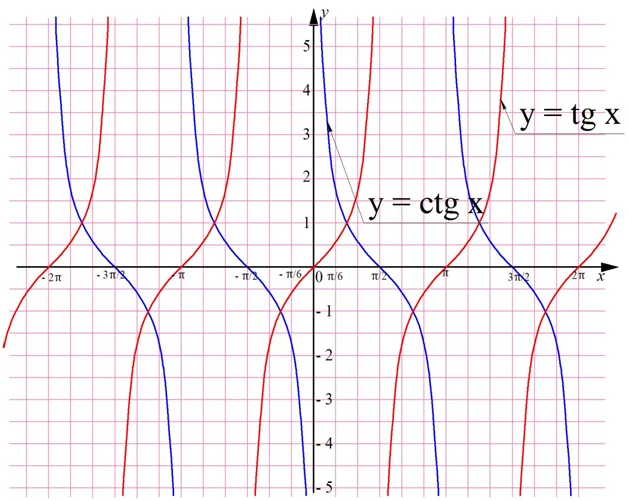
Котангенс, как и тангенс – нечетная ф-ция, то есть

ctg (– x) = – ctgx

Теперь у нас есть представление об основных тригонометрических ф-циях. Важнейшими из них являются синус и косинус. Тангенс является производной ф-цией от них и рассчитывается как отношение синуса к косинусу. Редко используемый котангенс, наоборот, представляет собой отношение косинуса к синусу.

Впервые элементы тригонометрии стали использовать ещё древние греки, которые производили с их помощью астрономические расчеты. В XVIII веке Эйлер сформулировал определения тригонометрических функций с помощью единичной окружности, благодаря которым стало возможным вычислять их значение для любых углов. Изначально тригонометрия использовалась для географических расчетов и навигации, однако со временем область ее применения расширилась. Оказалось, что без неё не обойтись в анализе финансовых рынков и биологических процессов, архитектуре, акустике и оптике, теории вероятностей.

Сумма, разность и произведение синуса и косинуса

Нам осталось разобрать еще несколько формул. В этот раз они связаны с действиями, производимыми с самими функциями. Например, с произведением синуса и косинуса. 

Рассмотрим формулы:

\(sin\alpha+sin \beta =2sin(\frac{\alpha+\beta}{2})*cos(\frac{\alpha-\beta}{2})\)\(sin \alpha-sin \beta=2sin(\frac{\alpha-\beta}{2})*cos(\frac{\alpha+\beta}{2})\)\(cos \alpha+cos \beta =2cos(\frac{\alpha-\beta}{2})*cos(\frac{\alpha+\beta}{2})\)\(cos \alpha-cos \beta =-2sin(\frac{\alpha+\beta}{2})*sin(\frac{\alpha-\beta}{2})\)\(sin \alpha*sin \beta =\frac{1}{2}(cos(\alpha-\beta)-cos(\alpha+\beta))\)\(cos \alpha*cos \beta =\frac{1}{2}(cos(\alpha-\beta)+cos(\alpha+\beta))\)\(sin \alpha*cos \beta=\frac{1}{2}(sin(\alpha-\beta)+sin(\alpha+\beta))\)

Заметим, что в формулах разные аргументы. Если они не табличные, то посчитать значение выражения почти нереально. Поэтому, если это возможно, с помощью этих формул мы можем упростить выражение до табличных углов.

Например, попробуем преобразовать выражение \(sin(\frac{3\pi}{8})*cos(\frac{\pi}{8})\). 

Рассчитать значение не представляется возможным: в аргументе стоят нетабличные значения. Попробуем преобразовать это выражение с помощью формулы \(sin \alpha*cos\beta =\frac{1}{2}(sin(\alpha-\beta)+sin(\alpha+\beta))\):

\(sin(\frac{3\pi}{8})*cos(\frac{\pi}{8})=\frac{1}{2}(sin(\frac{3\pi}{8}-\frac{\pi}{8})+sin(\frac{3\pi}{8}+\frac{\pi}{8}))\)

Преобразуем выражения в аргументах синусов отдельно:

\(\frac{3\pi}{8}-\frac{\pi}{8}=\frac{3\pi-\pi}{8}=\frac{2\pi}{8}=\frac{\pi}{4}\)\(\frac{3\pi}{8}+\frac{\pi}{8}=\frac{3\pi+\pi}{8}=\frac{4\pi}{8}=\frac{\pi}{2}\)

Получаем выражение:

\(\frac{1}{2}(sin(\frac{3\pi}{8}-\frac{\pi}{8})+sin(\frac{3\pi}{8}+\frac{\pi}{8}))=\frac{1}{2}(sin(\frac{\pi}{4})+sin(\frac{\pi}{2}))\)

Теперь подставим значения из таблицы:

\(\frac{1}{2}(sin(\frac{\pi}{4})+sin(\frac{\pi}{2}))=\frac{1}{2}(\frac{\sqrt2}{2}+1)=\frac{1}{2}*\frac{2+\sqrt2}{2}=\frac{2+\sqrt2}{4}\)

Значение выражения найдено.

Подведем итог. Формулы тригонометрии необходимы для преобразования сложных выражений. А чтобы они были в одном месте, мы составили для вас таблицу.

Итак, мы разобрались, как преобразовывать выражения с тригонометрическими функциями. Какой следующий шаг? Правильно, решение уравнений.

Расчет тангенса и котангенса в компьютерных программах

Тангенс и котангенс: что это такое?

Тангенс и котангенс — это тригонометрические функции, которые используются для нахождения соотношений между двумя сторонами прямоугольного треугольника.
Тангенс определяется как отношение противоположного катета к прилежащему, а котангенс как отношение прилежащего катета к противоположному.

В компьютерных программах расчет тангенса и котангенса выполняется с помощью математических функций. Обычно это функции «tan» и «cot». Например, если нужно найти тангенс угла в радианах, можно использовать следующий код: tan(x), где «x» — значение угла в радианах.

Зачем нужны тангенс и котангенс в компьютерных программах?

Тангенс и котангенс могут использоваться во многих приложениях, где необходимо вычислить углы или расстояния между объектами. Например, в компьютерной графике тангенс используется для определения наклона линий и кривых. В астрономии тангенс используется для нахождения высоты объектов на небосводе. Котангенс же применяется для определения угла наклона плоскости.

Также тангенс и котангенс могут использоваться в физике, инженерных расчетах и других научных приложениях

Важно понимать, что правильный расчет тангенса и котангенса может существенно влиять на точность результатов, поэтому необходимо использовать соответствующие математические функции и учитывать единицы измерения

Тангенс и котангенс нужны для решения задач, где требуется найти угол между двумя линиями или найти расстояние между двумя точками. В геометрии тангенс и котангенс используются для вычисления высоты, основания, площади и объема различных геометрических фигур.

Тангенс и котангенс: каковы их различия и зачем нужны

В геометрии довольно часто приходится сталкиваться с задачами, для решения которых необходимо знание тангенса и котангенса. Эти две математические функции очень важны как для геометрических вычислений, так и для работы в ряде других областей науки и техники.

Тангенс и котангенс являются соответственно функциями тригонометрии синуса и косинуса, разделяющихся каждая своей обратной функцией. Тангенс и котангенс — это отношения двух катетов в прямоугольном треугольнике, примыкающих к углу α и называемого соответственно катетом противоположным и катетом прилежащим.

Тангенс и котангенс находят применение в вычислениях астрономических координат, математической статистике, вероятности, физике, инженерии и многих других областях. Например, в радиотехнике тангенс и котангенс используются для вычисления импеданса и проводимости сигналов. В машиностроении они используются для нахождения углов наклона поверхностей и степени прессовки сжатых материалов.

Тангенс – это отношение стороны прямоугольного треугольника, противоположной заданному углу, к прилежащей стороне. Применение тангенса может быть очень разнообразным, он используется для решения уравнений, нахождения длины сторон треугольника, векторов, скорости и т. д.

Практическое применение тангенса и котангенса в физике и инженерии

Также котангенс применяется в оптике при расчетах нахождения фокусных расстояний линз.

06.06.2019 19:36:58

2019-06-06 19:36:58

Любые данныеЛюбые данныеЛюбые данные Любые данные

Применение функции тангенса для решения задач

Что бы научиться пользоваться этой функцией, Нужно попробовать решить несколько примеров по применению этой функции.

Первая формула, это tg α = а : b. тогда tg α = 7 :12= 0, 5833, далее для нахождения угла α используем таблицы Брадиса. На пересечении градусов и минут находим ближайшее значение угла – 0,5844, соответствующее 30° и 18′.

Находим ближайшую поправку, разную 3′. Отнимаем ее от нашего угла и получаем угол α = 30° 15′. Второй угол находим, исходя из того, что сумма всех углов должна быть не больше 180°, а угол γ = 90° по условию. Тогда угол β = 90° – 30° 15′= 59°45′.

Нам осталось найти гипотенузу с.

Можем найти её через sin α, который равен а: с, тогда с = а : sin α.

Находим sin α через таблицу Брадиса. Ближайшее значение 30° 36′, будет 0,5060, тогда не хватает 3′, Что по полям поправок равно 0,0008. Добавляем это число к найденному: 0, 5060 + 0,0008 = 0,5068. Подставляем это значение в формулу, с = 7:0,5068, с = 13, 8 см. Задача решена.

Можно искать значение углов через значение числа π, которое равно 180°. Тогда наиболее популярные углы, такие, как тангенс 30 градусов, тангенс 0 градусов, тангенс 60 градусов, тангенс 90 градусов, тангенс 45 градусов, тангенс 15 градусов, тангенс 75 градусов можно рассматривать намного проще. Нужно знать, что тангенс 0 градусов равен 0, а тангенс 90 градусов не имеет конкретного значения.

Можно найти тангенс угла 5 градусов, который равен 0, 0875 и добавлять или отнимать от наиболее часто встречающихся углов. Например угол 45 градусов, его тангенс равен 1, тогда тангенс угла 50 градусов будет равен 1, 0875. Тангенс 35 градусов можно рассчитать путем добавления к тангенсу 30 градусов угол 5 градусов, а тангенс 10 градусов это удвоение угла 5 градусов.

Для удобства есть рассчитанная таблица основных углов через значение π.

Значение угла α (градусов)	Значение угла α в радианах	tg (тангенс)
Тангенс 0
Тангенс 15	π/12	0.2679
Тангенс 30	π/6	0.5774
Тангенс 45	π/4	1
Тангенс 50	5π/18	5114
Тангенс 60	π/3	1.7321
Тангенс 65	13π/36	2.1445
Тангенс 70	7π/18	2.7475
Тангенс 75	5π/12	3.7321
Тангенс 90	π/2	–
Тангенс 105	5π/12	-3.7321
Тангенс 120	2π/3	-1.7321
Тангенс 135	3π/4	-1
Тангенс 140	7π/9	-0.8391
Тангенс 150	5π/6	-0.5774
Тангенс 180	π
Тангенс 270	3π/2	–
Тангенс 360	2π

Если угол больше 90 градусов, нужно помнить, что функции имеют свойство повторяться, поэтому, если ищем тангенс 145 градусов, тогда 180 – 145 = 35 градусов, но уже со знаком «минус», это можно понять по чертежу окружности, где положительное или отрицательное значение абсциссы и ординаты. Научиться быстро пользоваться таблицами Брадиса и рассчитывать значения треугольника совсем не сложно, главное, уловить суть процесса.