Что такое синус, косинус, тангенс и котангенс

Ключевые определения

Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $\alpha $:

Мы видим, что острый угол $\alpha $ образован гипотенузой $c$ и катетом $b$. Такой катет будем называть прилежащим. А катет $a$, который не участвует в формировании угла $\alpha $, назовём противолежащим:

Это общепринятые названия: как только в прямоугольном треугольнике отмечен острый угол, для него немедленно можно указать прилежащий катет и противолежащий. И тут мы переходим к ключевым определениям.

1.1. Синус, косинус, тангенс, котангенс

Итак, пусть дан прямоугольный треугольник с острым углом $\alpha $.

Тогда:

Вот так всё просто! Берём один катет, делим его на гипотенузы (или на другой катет) — и получаем выражение для синуса, косинуса, тангенса и котангенса. Все эти выражения называются тригонометрическими («тригонометрия» = «треугольники измеряю»).

Рассмотрим пару примеров.

Далеко не всегда будут получаться такие красивые ответы. Чаще они будут содержать корни — это следствие теоремы Пифагора

Но важно понимать: как только мы находим длины катетов и гипотенузу, мы сразу можем найти и синусы, косинусы, тангенсы

Далее в примерах мы не будем считать котангенсы, потому что из формулы котангенса очевидно, что они легко выражаются через тангенсы:

Но об этом чуть позже.

Простое правило, чтобы не запутаться, где прилежащий катет, а где противолежащий. Просто помните: приставка «ко» означает «вместе», «сообща». Поэтому «косинус» — это «катет, лежащий рядом, к гипотенузе», «котангенс» — это «катет, лежащий рядом, к противолежащему». И никак иначе.:)

1.2. Задачи для тренировки

Перед тем как переходить к следующей части урока, предлагаю 4 примера для тренировки.

Как видим, считать синусы, косинусы и тангенсы совсем несложно

Перейдём теперь к принципиально важному вопросу: а зачем вообще всё это нужно?

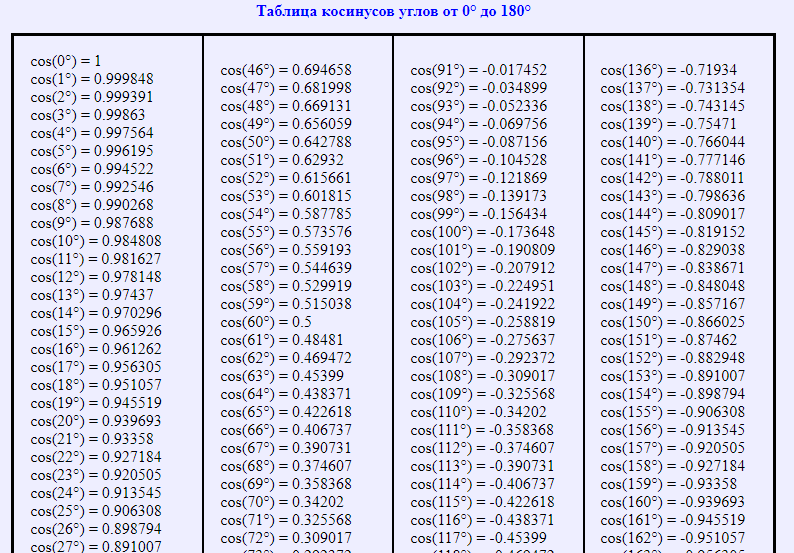
Таблица косинусов от 0° до 180°

Градусы, минуты и секунды являются общеизвестными измерительными единицами, предусмотренными для плоских углов. Угол в 360° соответствует одному полному обороту.

Градусы допустимо выражать в радианах и наоборот. Этот прием полезен для упрощения вычислений при решении задач с плоскими углами. Запишем справедливое соотношение, которое выражает зависимость между данными угловыми мерами:

$1^{\circ }={\frac {2\pi }{\displaystyle {360}}} радиан ={\frac {\pi }{\displaystyle {180}}}={\frac {1}{\displaystyle {p}}}\approx {\frac {1}{\displaystyle {57{,}295779513^{\circ }}}}{\displaystyle \approx 0{,}0174532925}$

Связь cos угла с тригонометрическим кругом

Косинус угла в тригонометрии определяется как отношение длины стороны прилежащей к данному углу в прямоугольном треугольнике к гипотенузе этого треугольника.

Тригонометрический круг, также известный как единичная окружность, является графическим представлением всех возможных синусов и косинусов углов. Стартовой точкой на круге является точка (1,0), соответствующая углу 0 градусов или 0 радиан. Вокруг центра окружности проводятся углы, а точка на окружности, соответствующая данному углу, определяет значение его косинуса.

На тригонометрическом круге значение косинуса угла можно определить по горизонтальной координате точки на окружности, соответствующей этому углу. Так, например, точка на круге, находящаяся в точке (0,-1), соответствует углу 90 градусов или π/2 радиан, и ее косинус равен 0. Аналогично, точка (-1,0), соответствующая углу 180 градусов или π радиан, имеет косинус равный -1.

Функция y = cos x, её свойства и график

Рассмотрим, как изменяется косинус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=cosx на этом отрезке.

Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривая продолжится влево.

В результате получаем график y=cosx для любого $x\in\mathbb$.

Заметим, что термин «косинусоида» используется достаточно редко. Обычно, и в случае косинуса, говорят о «синусоиде».

п.2. Свойства функции y=cosx⁡

1. Область определения $x\in\mathbb$ — множество действительных чисел.

2. Функция ограничена сверху и снизу $$ -1\leq cosx\leq 1 $$ Область значений $y\in$

3. Функция чётная $$ cos(-x)=cosx $$

4. Функция периодическая с периодом 2π $$ cos(x+2\pi k)=cosx $$

5. Максимальные значения $y_=1$ достигаются в точках $$ x=2\pi k $$ Минимальные значения $y_=-1$ достигаются в точках $$ x=\pi+2\pi k $$ Нули функции $y_=cosx_0=0$ достигаются в точках $x=\frac\pi2 +\pi k$

6. Функция возрастает на отрезках $$ -\pi+2\pi k\leq x\leq 2\pi k $$ Функция убывает на отрезках $$ 2\pi k\leq x\leq\pi+2\pi k $$

7. Функция непрерывна.

п.3. Примеры

Пример 1. Найдите наименьшее и наибольшее значение функции y=cosx на отрезке:a) $\left$ $$ y_=cos\left(\frac\right)=-\frac>,\ \ y_=cos\left(\frac\pi6\right)=\frac> $$ б) $\left$ $$ y_=cos(\pi)=-1,\ \ y_=cos\left(\frac\right)=\frac12 $$

Пример 2. Решите уравнение графически:a) $cosx=\frac\pi2-x$Один корень: $x=\frac\pi2$

б) $cosx-x=1$$cosx=x+1$Один корень: x = 0

в) $cosx-x^2=1$$cosx=x^2+1$ Один корень: x = 0

г*) $cosx-x^2+\frac=0$$cosx=x^2-\frac$$y=x^2-\frac$ – парабола ветками вверх, с осью симметрии $x_0=0$ (ось OY) и вершиной $\left(0; -\frac\right)$ (см. §29 справочника для 8 класса)Два корня: $x_=\pm\frac\pi2$

Пример 3. Постройте в одной системе координат графики функций $$ y=cosx,\ \ y=-cosx,\ \ y=2cosx,\ \ y=cosx-2 $$ $y=-cosx$ – отражение исходной функции $y=cosx$ относительно оси OX. Область значений $y\in$.$y=2cosx$ – исходная функция растягивается в 2 раза по оси OY. Область значений $y\in$.$y=cosx-2$ — исходная функция опускается вниз на 2. Область значений $y\in$.

Пример 4. Постройте в одной системе координат графики функций $$ y=cosx,\ \ y=cos2x,\ \ y=cos\frac $$ Амплитуда колебаний у всех трёх функций одинакова, область значений $y\in$.Множитель под косинусом изменяет период колебаний.$y=cosx$ – главная арка косинуса соответствует отрезку $-\frac\pi2\leq x\leq\frac\pi2$$y=cos2x$ — период уменьшается в 2 раза, главная арка укладывается в отрезок $-\frac\pi4\leq x\leq\frac\pi4$.$y=cos\frac$ — период увеличивается в 2 раза, главная арка растягивается в отрезок $-\pi \leq x\leq \pi$.

Ограничения косинуса: что нужно знать об ограничениях этой математической функции?

Косинус — это математическая функция, определенная для всех действительных чисел

Однако, у нее существуют определенные ограничения, которые важно знать

Ограничения диапазона значений:

Диапазон значений косинуса ограничен от -1 до 1.
Косинус принимает значение -1 при аргументе π, которое является наиболее негативным значением.
Косинус равен 1 при аргументе 0, что является наиболее позитивным значением.

Ограничения периода:

Период косинуса равен 2π, что означает, что функция повторяется каждые 2π единиц аргумента.
Также можно выразить период косинуса как 360 градусов.

Ограничения графика:

График косинуса формирует волну с периодом 2π, которая повторяется в течение всего диапазона значений.
График представляет собой периодическую функцию с симметрией относительно оси абсцисс.
Максимальные значения функции находятся в точках, где аргумент косинуса равен 0 (аргумент функции смещен на 90 градусов и изменяется от 0 до 2π).
Минимальные значения функции достигаются в точках, где аргумент косинуса равен π (аргумент функции смещен на 90 градусов и изменяется от 0 до 2π).

Понимание этих ограничений косинуса позволит вам более точно работать с этой функцией и применять ее в различных математических задачах и приложениях.

Определения тригонометрических функций

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Важно помнить!

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1.

Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов. Угол поворота в градусах или радианах выражается любым действительным числом от .

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0; 1) и (0; -1). В таких случаях выражение для тангенса просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

Важно помнить!

Синус и косинус определены для любых углов .

При решении практических примеров не говорят «синус угла поворота «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом числа называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в радиан.

Например, синус числа равен синусу угла поворота величиной рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Начальная точка на окружности — точка A c координатами (1;0).

Положительному числу соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь длиной .

Отрицательному числу соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь длиной ||.

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу , совпадает с точкой, в которую переходит начальная точка после поворота на угол радиан.

Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент.

Взгляните:

Синим цветом обозначено положительное направление оси (ось ординат), красным — положительное направление оси (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными.

В частности,

Для наглядности отметим знаки каждой тригонометрической функции — синуса, косинуса и тангенса — на отдельных «радарах». Получим следующую картинку:

Знаки котангенса совпадают со знаками тангенса — никаких специальных правил там нет.

Таблица значений синусов, косинусов, тангенсов и котангенсов для основных углов.

Квадрат косинуса и его интерпретация

cos^2(a) = (cos(a))^2

Для начала давайте вспомним, что такое косинус. Косинус – это тригонометрическая функция, которая принимает значения от -1 до 1 и определяется в прямоугольном треугольнике как отношение прилежащего катета к гипотенузе. Как мы знаем, угол может быть острым, прямым, тупым или полным.

Теперь вернемся к формуле и посмотрим, чему равен квадрат косинуса. Если взять косинус угла и возвести его в квадрат, то мы получим значение, которое также находится в интервале от 0 до 1. Это значит, что квадрат косинуса всегда положителен и находится в пределах от 0 до 1. Если квадрат косинуса угла равен 1, то значит, что сам косинус угла равен 1. В случае, если квадрат косинуса угла равен 0, значит, что сам косинус угла равен 0.

Важно отметить, что значение квадрата косинуса угла может быть использовано для интерпретации степени сходства между двумя векторами. Более конкретно, значение квадрата косинуса угла между двумя векторами является мерой их сходства или корреляции

Чем ближе значение квадрата косинуса угла к 1, тем более похожи векторы между собой. Если же значение ближе к 0, то можно сказать, что векторы имеют слабую корреляцию.

Также стоит отметить, что квадрат косинуса угла может быть использован в различных областях, таких как физика, инженерия, компьютерная графика и других. В этих областях он используется для вычисления различных параметров и определения свойств объектов или явлений. Например, в компьютерной графике квадрат косинуса угла может использоваться для определения теней и освещения объектов на экране.

В итоге, квадрат косинуса угла является мощным математическим инструментом, который позволяет вычислять значение косинуса угла, возведенного в квадрат. Он имеет широкий спектр применения и может быть использован для анализа сходства векторов и определения свойств объектов в различных областях знаний.

Синус, косинус и тангенс острого угла прямоугольного треугольника

Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.

Острый угол — меньший 90 градусов.

Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается

Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается

Угол обозначается соответствующей греческой буквой .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла , называется противолежащим (по отношению к углу ). Другой катет , который лежит на одной из сторон угла , называется прилежащим.

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:

Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):

Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач

Давайте докажем некоторые из них.

Сумма углов любого треугольника равна . Значит, сумма двух острых углов прямоугольного треугольника равнa .
С одной стороны, как отношение противолежащего катета к гипотенузе. С другой стороны, , поскольку для угла катет а будет прилежащим.Получаем, что . Иными словами, .
Возьмем теорему Пифагора: . Поделим обе части на : Мы получили основное тригонометрическое тождество.
Поделив обе части основного тригонометрического тождества на , получим: Это значит, что если нам дан тангенс острого угла , то мы сразу можем найти его косинус. Аналогично,

Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?

Мы знаем, что сумма углов любого треугольника равна .

Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .

Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.

Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.

Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до .

−

Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют

Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.

1. В треугольнике угол равен , . Найдите .

Задача решается за четыре секунды.

2 . В треугольнике угол равен , , . Найдите .

Найдем по теореме Пифагора.

Часто в задачах встречаются треугольники с углами и или с углами и . Основные соотношения для них запоминайте наизусть!

Для треугольника с углами и катет, лежащий напротив угла в , равен половине гипотенузы.

Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.

Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.

Как выразить значение функции косинуса через ряд Фурье?

Одним из способов выразить значение функции косинуса является использование ряда Фурье. Ряд Фурье представляет функцию в виде бесконечной суммы синусов и косинусов, которые имеют различные амплитуды и частоты.

Ряд Фурье для функции косинуса:
cos(x) = 1/2 * a₀ + ∑(n=1, ∞)

В данном выражении a₀, aₙ и bₙ — это коэффициенты ряда Фурье, которые можно вычислить с помощью интегралов или специальных формул.

Выполнив подстановку конкретных значений a₀, aₙ и bₙ в ряд Фурье, можно получить выражение для функции косинуса в виде суммы синусов и косинусов. Это выражение позволяет точно вычислить значение функции косинуса для любого заданного угла.

Таким образом, использование ряда Фурье позволяет выразить функцию косинуса более общим образом и подходит для решения более сложных математических задач.

Определение синуса и косинуса

Синус угла в треугольнике определяется как отношение противолежащей стороны к гипотенузе:

sin(угол) = противолежащая сторона / гипотенуза

Косинус угла в треугольнике определяется как отношение прилежащей стороны к гипотенузе:

cos(угол) = прилежащая сторона / гипотенуза

В обоих определениях гипотенуза – самая длинная сторона треугольника, противолежащая сторона – сторона, противоположная углу, а прилежащая сторона – сторона, прилегающая к углу.

Значения синуса и косинуса лежат в интервале от -1 до 1 и зависят от величины угла. Они могут быть представлены в виде десятичных дробей или в виде тригонометрических таблиц.

Синус и косинус широко используются для решения задач, связанных с геометрией, механикой, астрономией и другими науками. Они могут быть использованы для вычисления длин векторов, нахождения расстояний, определения направлений движения и других задач, связанных с треугольниками и углами.

Синус:

Синус широко используется в математике, физике и других науках, а также в различных областях жизни для описания осцилляций и периодических явлений. Например, при изучении звуковых волн, колебаний пружин и электромагнитных колебаний синус-функция используется для описания распределения значений во времени или пространстве.

Также синус может быть использован для решения различных задач, связанных с треугольниками, таких как нахождение длины сторон прямоугольного треугольника или углов по известным сторонам и углам.

Другой пример использования синуса — в компьютерной графике и компьютерной графике. Синус-функция используется для создания плавных переходов и анимаций, а также для моделирования трехмерных объектов и создания реалистичных эффектов.

Формула синуса:

sin(α) = a / c

где α — один из углов прямоугольного треугольника, a — противоположный катет и c — гипотенуза.

Косинус:

Косинус является периодической функцией со значениями от -1 до 1, где cos(0) = 1. Основное свойство косинуса заключается в том, что он является четной функцией, то есть cos(-x) = cos(x).

Косинус широко используется в различных областях науки и техники. Например, в физике косинус используется для решения задач, связанных с колебаниями и волной. Также косинус применяется в математике для решения уравнений и построения графиков. В программировании косинус часто используется для вычисления значения трехмерных векторов и работы с графиками.

Пример использования косинуса: представим, что у нас есть прямоугольный треугольник с углом x. Если известна длина гипотенузы и угол x, то можно использовать косинус, чтобы найти длину прилежащего катета. Например, если гипотенуза равна 10 и угол x равен 60 градусам, то косинус 60 градусов равен 0.5, что означает, что прилежащий катет равен половине длины гипотенузы, т.е. 5.

Использование cos угла в математике и физике

В математике функция cos(x) позволяет вычислить значение косинуса угла x в радианах. Косинус является периодической функцией с периодом 2π и может принимать значения от -1 до 1. Она играет важную роль в тригонометрии и геометрии, позволяя решать задачи, связанные с измерением углов, нахождением длин сторон треугольников и других геометрических фигур.

В физике cosинус угла используется для описания и измерения различных физических явлений. Например, в механике он применяется для анализа движения тела по окружности или гармонических колебаний. В электротехнике его используют для описания периодических сигналов или анализа электрических колебаний. Волновая оптика использует cosинус для расчетов интерференции и дифракции световых волн.

Также cosинус угла широко используется в математическом моделировании и компьютерной графике. Он позволяет реализовывать различные эффекты, такие как прозрачность, освещение и тени, создавая более реалистические изображения и анимацию.

Практические применения косинуса

Косинус в геометрии

Косинус широко используется в геометрии для вычисления расстояний, углов и других параметров треугольников и многоугольников. Он помогает нам понять и анализировать формы и структуры объектов в пространстве.

Косинус в физике

В физике косинус используется для моделирования и анализа различных физических явлений. Он позволяет нам изучать движение, взаимодействие объектов и предсказывать результаты экспериментов.

Косинус в компьютерной графике

В компьютерной графике косинус применяется для создания реалистичных 3D моделей, анимации и эффектов. Он помогает определить положение, освещение и цвет объектов на экране, что делает изображения и видео более привлекательными и реалистичными.

Как найти значение функции косинуса градуса?

Для нахождения значения функции косинуса градуса необходимо выполнить следующие шаги:

Убедитесь, что угол выражен в градусах.
Найдите значение косинуса на основе таблицы или калькулятора.
Если таблицы или калькулятора нет, используйте приближенное значение с помощью формулы или программного кода.

Допустим, у нас есть угол 30 градусов. Чтобы найти значение косинуса этого угла, мы можем использовать таблицу значений тригонометрических функций или специальный калькулятор. В таблице или калькуляторе мы найдем значение, соответствующее 30 градусам. Например, значение косинуса 30 градусов равно 0.866.

Если у вас нет доступа к таблице или калькулятору, вы можете использовать приближенное значение косинуса с помощью формулы или программного кода. Для этого вы можете использовать ряд Маклорена для приближенного вычисления косинуса угла. Формула будет выглядеть следующим образом:

Если вы работаете с программированием, вы можете воспользоваться специальными математическими функциями или библиотеками, которые предоставляют возможность вычислить значение косинуса угла по его аргументу в градусах.

Теперь, когда вы знаете, как найти значение функции косинуса градуса, вы можете приступить к решению задач, требующих вычисления косинуса угла. Помните, что использование правильного значения косинуса является важным при выполнении математических расчетов и измерений.