Многомерные пространства

Значение 3D прямоугольников в различных областях

3D прямоугольники имеют широкое применение в различных областях, включая компьютерную графику, архитектуру и дизайн. Благодаря своей трехмерной форме, они предоставляют возможность визуализации и моделирования объектов, которые имеют прямоугольное основание и высоту.

Компьютерная графика:

• 3D прямоугольники используются для создания и анимации объектов в компьютерных играх и фильмах. Они позволяют создавать реалистичные сцены и персонажей, добавлять текстуры и освещение.
• Также 3D прямоугольники используются в 3D моделировании и виртуальной реальности. Они позволяют создавать и манипулировать трехмерными моделями, отображать их в разных ракурсах и углах обзора.
• В архитектуре 3D прямоугольники используются для создания трехмерных моделей зданий и интерьеров. Это позволяет архитекторам представить проекты клиентам и визуализировать конечный результат.

Дизайн и искусство:

• 3D прямоугольники могут использоваться в дизайне упаковки, логотипов и рекламных материалов. Они добавляют объемности и глубины дизайну, делая его более привлекательным и запоминающимся.
• Также 3D прямоугольники могут быть использованы в скульптуре и инсталляциях. Они помогают создавать абстрактные формы и экспериментировать с объемом и структурой.
• Видеоигры и интерактивные искусство также активно используют 3D прямоугольники для создания трехмерных объектов и сцен.

Научные исследования и образование:

• 3D прямоугольники могут быть использованы для визуализации и анализа данных в научных исследованиях. Например, в медицине они используются для моделирования органов и тканей, что помогает в диагностике и планировании лечения.
• В образовании 3D прямоугольники могут быть использованы для обучения трехмерной геометрии и математике. Они помогают студентам лучше понять и визуализировать геометрические формы и свойства.

Таким образом, 3D прямоугольники играют важную роль во многих областях, обеспечивая возможность создания, моделирования и визуализации трехмерных объектов и сцен.

Определение и примеры

Примером геометрического тела является куб. Куб имеет шесть равных равносторонних граней, восемь вершин и двенадцать ребер. Другим примером геометрического тела является цилиндр. У цилиндра есть два основания, которые представляют собой круги, и боковая поверхность, которая представляет собой плоскость, параллельную основаниям. Цилиндр также имеет ребра, вершины и высоту.

Кроме куба и цилиндра, в группу геометрических тел входят также сфера, пирамида, конус, параллелепипед, призма и многие другие.

Название	Описание	Примеры
Куб	Фигура с шестью равными равносторонними гранями	Рубикова головоломка
Цилиндр	Тело, у которого два основания представляют собой круги, а боковая поверхность — плоскость, параллельная основаниям	Банка из-под газировки
Сфера	Тело, все точки которого равноудалены от центра	Мяч для боулинга
Пирамида	Тело, у которого одно из оснований является многоугольником, а боковые грани — треугольниками, соединяющими вершины основания с одной точкой — вершиной пирамиды	Египетская пирамида Хеопса
Конус	Тело, у которого одно основание является кругом, а боковая поверхность состоит из всех линий, соединяющих точки на окружности основания с вершиной конуса	Хвойное дерево
Параллелепипед	Тело, у которого все грани прямоугольники, а противоположные грани параллельны	Книга
Призма	Тело, у которого два основания являются одинаковыми многоугольниками, а боковые грани — прямоугольники, соединяющие соответствующие стороны оснований	Дом

Что представляет собой группа геометрических тел

Группа геометрических тел состоит из различных трехмерных фигур, которые имеют определенные свойства и характеристики.

В эту группу входят следующие тела:

• Параллелепипед — трехмерная фигура, у которой все грани являются прямоугольниками.
• Пирамида — многогранник с одной вершиной и множеством граней, которые сходятся к этой вершине.
• Цилиндр — тело, ограниченное двумя параллельными плоскостями (основаниями) и боковой поверхностью, представляющей собой закругленный прямоугольник.
• Конус — геометрическое тело, имеющее одно основание и вершину, к которой сходятся все стороны этого основания.
• Шар — сферическое тело, все точки поверхности которого равноудалены от центра.
• Тор — геометрическое тело, представляющее собой поверхность, получаемую вращением окружности вокруг своей оси.

Эти геометрические тела имеют различные формы и свойства. Они широко применяются в геометрии, физике, инженерии и других науках для моделирования и решения различных задач.

Примеры из группы геометрических тел

Группа геометрических тел включает в себя разнообразные объекты с определенными геометрическими формами и свойствами. Некоторые примеры таких тел:

1. Параллелепипед — это тело, имеющее шесть прямоугольных граней. Он образуется, когда на каждой стороне прямоугольника построена грань-прямоугольник, параллельная данной стороне.
2. Сфера — это тело, все точки которого находятся на одинаковом расстоянии от центра. Сфера обладает свойством симметрии и не имеет граней.
3. Цилиндр — это тело, имеющее две круглые грани, параллельные друг другу, и боковую поверхность, состоящую из плоской кривой.
4. Конус — это тело, у которого одна грань представляет собой плоскую кривую, а вторая грань — круг.
5. Пирамида — это тело, у которого одна грань является многоугольником, а все остальные грани — треугольники, соединяющие вершины многоугольника с одной точкой.

Это лишь некоторые примеры из многообразия геометрических тел, которые существуют в математике и геометрии.

Плоские геометрические фигуры

Круг — это геометрическое место точек на плоскости, расстояние от которых до его центра, не превышает заданного числа, называемого радиусом этого круга. Основной математической характеристикой круга является радиус.

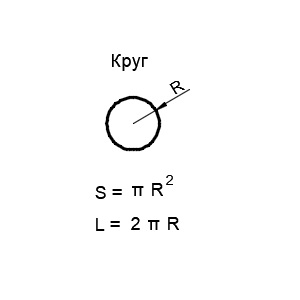
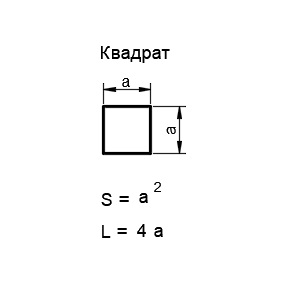
2. Квадрат

Квадрат — это четырёхугольник, у которого все углы и все стороны равны. Основной математической характеристикой квадрата является длина его стороны.

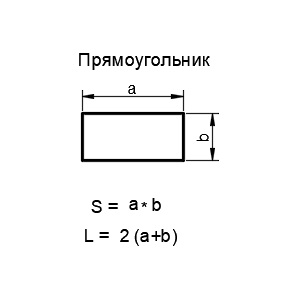
3. Прямоугольник

Прямоугольник — это четырехугольник, у которого все углы равны 90 градусам (прямые). Основными математичскими характеристиками прямоугольника являются длины его сторон.

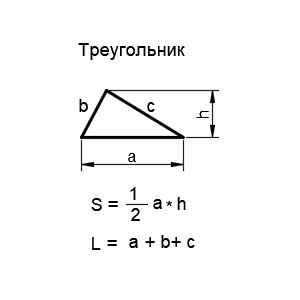
4. Треугольник

Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки (вершины треугольника), не лежащие на одной прямой. Основными математическими характеристиками треугольника являются длины сторон и высота.

5. Трапеция

Трапеция — это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Основными математическими характеристиками трапеции являются длины сторон и высота.

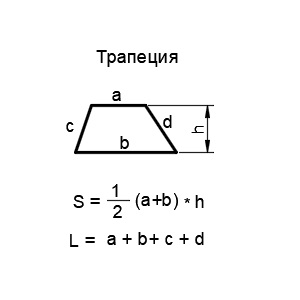
6. Параллелограмм

Параллелограмм — это четырёхугольник, у которого противоположные стороны параллельны. Основными математическими характеристиками параллелограмма являются длины его сторон и высота.

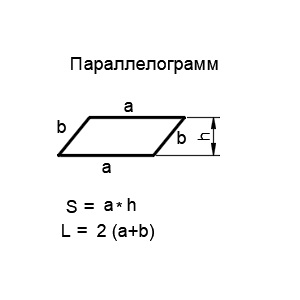
Ромб — это четырехугольник, у которого все стороны, а углы его вершин не равны 90 градусам. Основными математическими характеристиками ромба являются длина его стороны и высота.

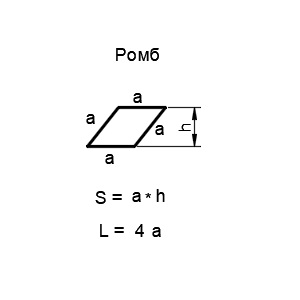
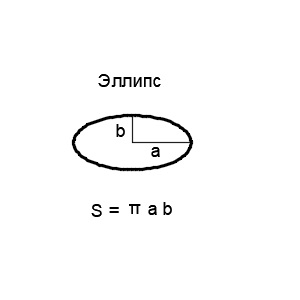
8. Эллипс

Эллипс — это замкнутая кривая на плоскости, которая может быть представлена как ортогональная проекция сечения окружности цилиндра на плоскость. Основными математическими характеристиками окружности являются длина его полуосей.

Что такое шар?

Свойство	Описание
Радиус	Расстояние от центра шара до любой точки его поверхности.
Диаметр	Удвоенное значение радиуса. Это самая длинная прямая линия, которую можно провести внутри шара, и она проходит через его центр.
Объем	Количество пространства, занимаемого шаром. Формула для вычисления объема шара: V = (4/3)πr³, где V — объем, r — радиус, π — математическая константа, примерно равная 3,14.
Площадь поверхности	Общая площадь всех поверхностей шара. Формула для вычисления площади поверхности: S = 4πr², где S — площадь поверхности, r — радиус, π — математическая константа, примерно равная 3,14.

Шары используются в различных областях, включая математику, физику, геометрию, астрономию, механику и технику. Они являются основными объектами при рассмотрении законов движения, взаимодействия и свойств материи.

В технике шары применяются в шариковых подшипниках, шариковых клапанах, а также в создании шаровых моделей и макетов для демонстрации определенных процессов и явлений. В астрономии шары используются для моделирования планет и других небесных тел, а также в исследовании структуры и эволюции Вселенной.

Кроме того, шары широко используются в различных видов спорта, таких как футбол, баскетбол, гольф и других, где они являются основными мячами для игры.

Определение шара

Параметр	Описание
Радиус	Расстояние от центра шара до любой точки его поверхности.
Диаметр	Удвоенное значение радиуса. Равен расстоянию между двумя точками на поверхности шара, проходящими через его центр.
Объем	Количество пространства, занимаемое шаром.
Площадь поверхности	Площадь внешней поверхности шара. Вычисляется по формуле S = 4πr^2, где r — радиус шара.

Шары находят широкое применение в различных областях, таких как геометрия, физика, инженерия, астрономия и технические науки. Они используются для моделирования сферических объектов, расчетов объемов, создания шаровых сегментов и сферических зон, а также для создания шарообразных конструкций в архитектуре и дизайне.

Структура шара

Основной элемент шара — сфера. Сфера представляет собой поверхность, все точки которой находятся на одинаковом расстоянии от ее центра. Она является внешней границей шара и определяет его форму.

Внутри сферы находится объем шара, который заполнен воздухом, газом или жидкостью. Этот объем представляет собой пространство, ограниченное сферической поверхностью.

Центр шара является точкой, которая находится в середине сферы. От центра до любой точки на сфере все расстояния одинаковые и равны радиусу шара — расстоянию от центра до поверхности.

Шары могут быть разных размеров и иметь разные радиусы в зависимости от их предназначения и области применения. Они широко используются в научных и технических областях, а также в различных игровых и спортивных занятиях.

Физические свойства шара

Основные физические свойства шара включают его диаметр, радиус и площадь его поверхности. Диаметр шара — это линия, проходящая через его центр и заканчивающаяся на противоположных сторонах поверхности. Радиус шара — это расстояние от центра до любой точки на его поверхности.

Площадь поверхности шара можно вычислить, используя формулу:

S = 4πr²

где S — площадь поверхности, π (пи) — математическая константа, примерное значение равно 3.14159, r — радиус шара.

Важной физической характеристикой шара является его объем. Объем шара можно определить по формуле:. V = (4/3)πr³

V = (4/3)πr³

где V — объем шара, π (пи) — математическая константа, примерное значение равно 3.14159, r — радиус шара.

Шары широко используются в различных областях, таких как геометрия, физика, астрономия и технические науки. Благодаря своим уникальным свойствам, шары могут быть использованы для моделирования и изучения различных процессов и явлений в природе и искусстве.

Приемы моделирования объектов

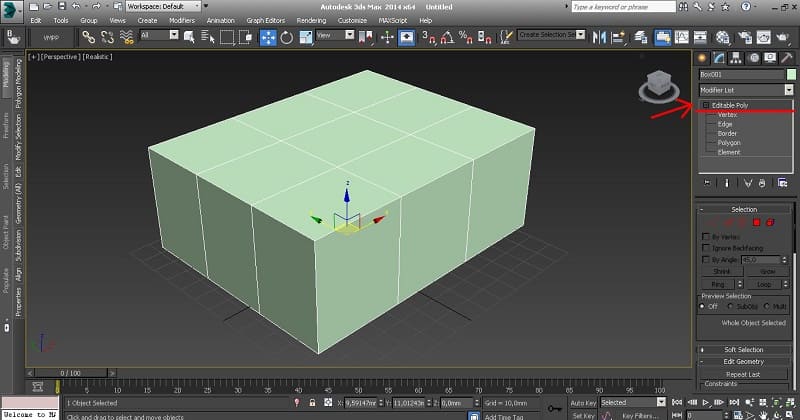
Конструирование с помощью вершин

Основу сетки составляют прямоугольные ячейки, каждая имеет свои вершины, с их помощью происходит редактирование. Что бы создать другой объект, необходимо произвести манипуляции с точками вершин.

 

В качестве наглядного примера, используется куб, затем, активировав F9, не снимая выделения, переходят в режим редактирования вершин. Задействовав инструмент Move Tool, верхние точки перемещаются, так, что бы примитив принял другую форму. При необходимости сохранить симметрию, удобней всего воспользоваться инструментом Scale Tool.  Воспользовавшись различными инструментами можно добиться совершенно уникальных результатов, например, при вращении, вершинах приобретут спиралевидную форму.

Кроме всего прочего, для вершин существует уникальный метод стёсывания, позволяющий создавать множество граней из одной.

Использование рёбер в проектировании

Этот метод схож с предыдущим, редактирование рёбер осуществляется по тому же принципу, что и с вершинами. На практике это работает следующим образом: в качестве базового элемента создаётся куб, при нажатии клавиш F10 активизируется редактор рёбер. Далее, в качестве примера вытягивается одна и противоположных граней ребра. После чего, появится дополнительная плоскость, такую же операцию можно повторить и с соседними рёбрами.

Проектирование моделей с помощью полигонов

Сразу стоит отметить, это наиболее распространённый метод создания сложных объёмных конструкций. В этом случае работа проводится с полигонами, производя различные манипуляции можно менять форму, размер, создавать более сложные объекты. Как и в предыдущих примерах, редактирование происходит по аналогичному сценарию. Активизировав клавишу F11, запускается редактирование полигонов, предварительно выделив один из примитивов, можно работать с гранями, меняя их положение.

Дополнительно доступно множество приёмов по преобразованию граней.

 

При разбивании грани на две части, создаётся ещё одно ребро. После активации команды правка, курсор мыши изменится, после этого стоит выделить вершины нового ребра и выйти из режима правки, кликнув на пустом поле. После этого можно совершать любые действия относительно новых рёбер.

Общая характеристика

В мире имеется множество предметов с формой параллелепипеда. Люди обычно не задумываются об этом, но архитектура и различные массивные строения состоят из нескольких граней. Выглядеть параллелепипед может по-разному в зависимости от типа.

Основные понятия и классификация

Определение параллелепипеда, пирамиды, куба и других многогранников было известно с древнейших времен. Основными характеристиками являются простота и значимость.

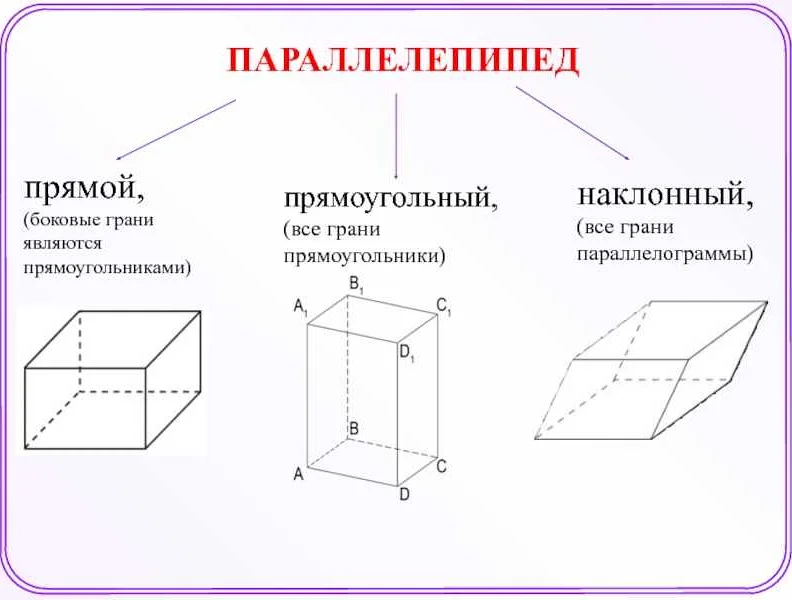
Выведенные формулы V и S значимы для решения различных задач с практическим содержанием и доказательства теорем (по чертежам). Виды параллелепипеда:

1. Прямой. Четыре боковые грани имеют углы по 90 градусов.
2. Прямоугольный. Каждая сторона фигуры является прямоугольной.
3. Наклонный.
4. Двугранный, трехгранный. Состоит из нескольких граней под углом 90 градусов.
5. Наклонный, диагональный. Боковые грани не перпендикулярны основаниям.
6. Ромбоэдр. Стороны являются одинаковыми ромбами.
7. Куб. Параллелепипед с равными (квадратными) сторонами.

Две стороны параллелепипеда, не имеющие общего ребра, называются противоположными, а содержащие единую линию — смежными. С точки зрения плоскостей, расположенных параллельно, внутри пересекаются три их пары. Эти вершины соединяет отрезок — диагональ. Длина трех ребер правильного многогранника называется измерением. Главным условием является общая вершина.

При решении задач важно понятие высоты — перпендикуляра, опущенного из любой вершины на обратную сторону. Грань, на которую опускается высота, считается основанием

Свойства параллелепипеда:

• любые стороны являются параллелограммами (с симметрией);
• стороны, расположенные друг против друга, будут параллельными и равными.

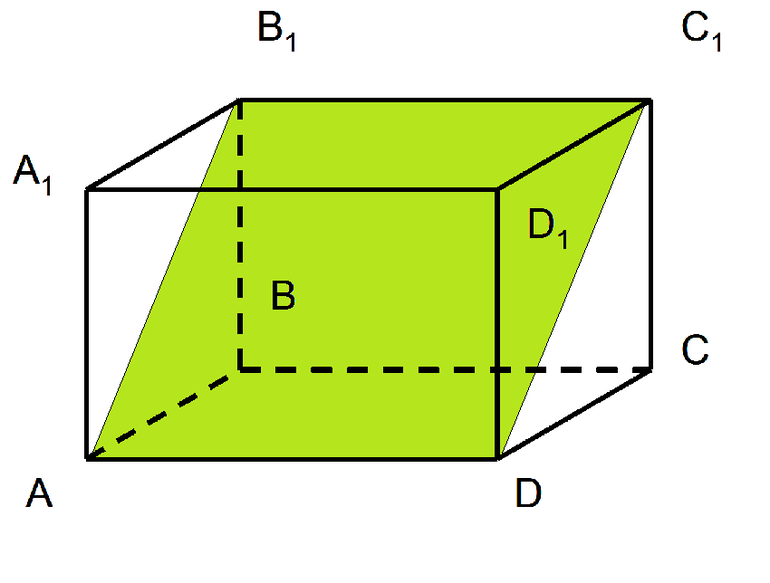
Кирпич — отличный пример прямоугольного параллелепипеда (ПП). Также его форму имеют девятиэтажные панельные дома, шифоньеры, шкафы-купе, контейнеры для хранения продуктов и прочие предметы быта.

Грани параллелепипеда спереди и сзади равнозначны, также как верхняя и нижняя стороны, но не равны, поскольку не противоположные, а смежные.

Формулы и анализ

Для ПП верно мнение, что его объем равен величине тройного произведения векторов трех сторон, исходящих из единой вершины. Формулы для ПП:

1. V=a*b*c.
2. S б =2*c*(a+b).
3. S п =2*(a*b+b*c+a*c).

Особым случаем параллелепипеда, в котором все стороны квадраты, является куб. Если любую из сторон обозначить буквой a, то для поверхности и объема используются формулы: S=6*a*2, V=3*а. В них V — объем фигуры, a — длина грани.

Последняя разновидность параллелепипеда — прямой тип. Его основанием будет параллелограмм, а основанием ПП — прямоугольник. Формулы, используемые в математике и геометрии: Sб=Ро*h, Sп=Sб+2Sо, V=Sо*h.

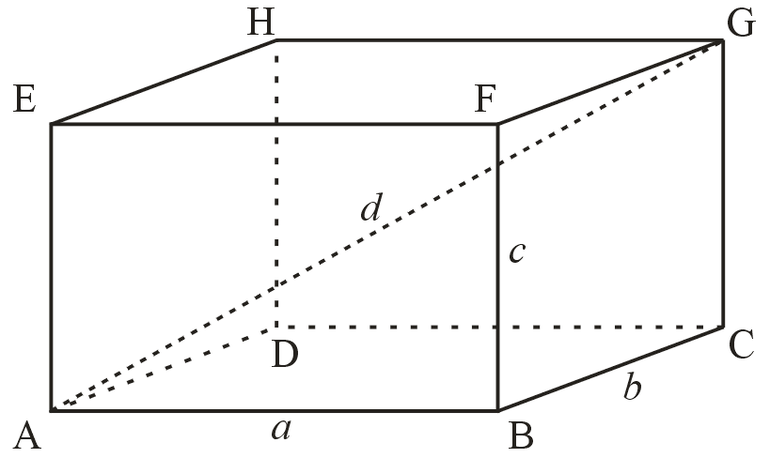
Диагональ ПП равна сложению квадратов его измерений: d2 = a2 + b2 + c2. Эта формула получается из теоремы Пифагора.

∆BAD — прямоугольный, поэтому BD2 = AB2 + AD2 = b2 + c2.

∆BDD1 является прямоугольным, значит, BD12 = BD2 + DD12. Нужно подставить значение: d2 = a2 + b2 + c2.

Стандартная формула: V= Sосн*h. Расшифровка обозначений: V — объем параллелепипеда, Sосн — площадь основания, h — высота.

S находится так же, как показатель параллелограмма или прямоугольника. При решении тестов и экзаменационных задач легче вычислять показатели призмы, в основе которой находится прямой угол. Также может пригодиться формула расчета стороны параллелепипеда Sбок = P*h, где:

• Sбок — площадь параллелепипеда;
• Р — периметр;
• h — высота, перпендикулярная основанию.

Свойства параллелепипеда 5 класс

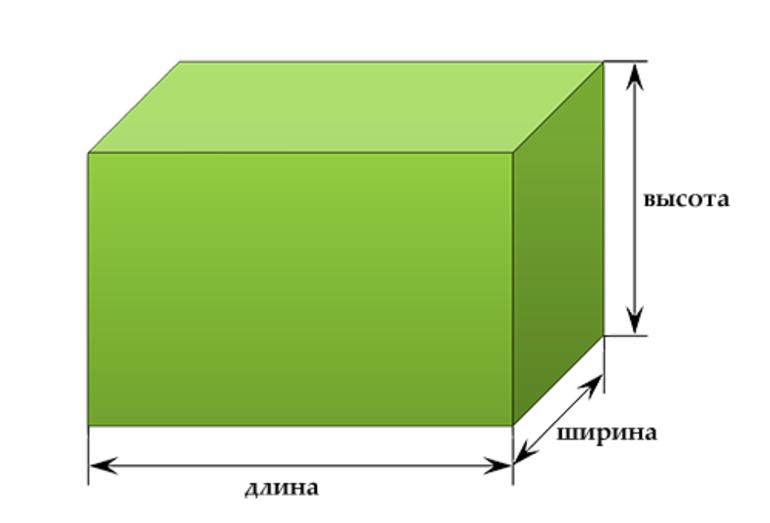
Параллелепипед — это геометрическое тело, у которого все грани являются прямоугольниками, а противоположные грани параллельны.

У параллелепипеда есть несколько свойств:

1. Параллельные грани: у параллелепипеда все грани являются прямоугольниками, и каждая грань параллельна своей противоположной грани.
2. Ребра и рёберная сетка: у параллелепипеда шесть рёбер, а рёберная сетка параллелепипеда образована всеми его рёбрами.
3. Диагонали: параллелепипед имеет три пары противоположных диагоналей. Всего у параллелепипеда шесть диагоналей.
4. Базы: основания параллелепипеда — это две противоположные параллельные грани.
5. Высота: высотой параллелепипеда называется расстояние между его основаниями. Она перпендикулярна плоскости основания и проходит через центр масс параллелепипеда.
6. Объём: объём параллелепипеда равен произведению длины, ширины и высоты.

Свойства параллелепипеда помогают нам лучше понять его форму и особенности. Изучение этих свойств позволяет решать задачи, связанные с параллелепипедом и использовать его в практических ситуациях.

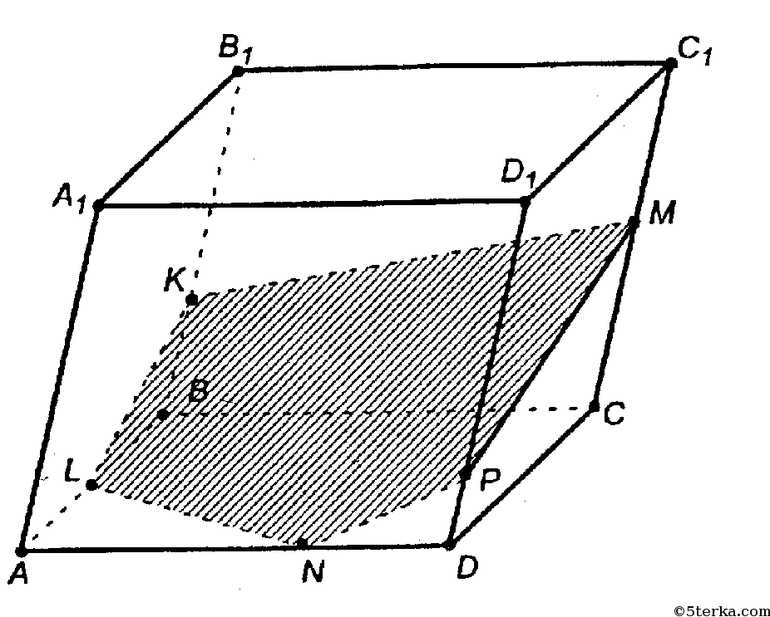
Свойства параллелепипеда, какими обладают противолежащие грани

Вне зависимости от вида параллелепипеда, все они обладают 4 свойствами:

1. Противолежащие грани равны друг другу и попарно параллельны.
2. Все 4 диагонали шестигранника пересекаются в одной точке, которой делятся пополам. Любой отрезок, проходящий через середину диагонали, и концы которого принадлежат поверхности, также делится пополам.
3. Фигура симметрична относительно середины диагонали.
4. Квадрат длины диагонали равен сумме квадратов трех измерений.

Прямоугольный параллелепипед обладает всеми этими свойствами и несколькими специфичными, свойственными только ему.

1. Все стороны — прямоугольники.
2. Все углы, состоящие из двух граней, равны 90°.
3. Любую сторону можно принять за основание.
4. Если все ребра равны и перпендикулярны, то такой шестигранник считается кубом.

Виды объемных прямоугольников

Объемный прямоугольник, известный также как параллелепипед, является фигурой, состоящей из шести прямоугольных граней. Прямоугольник может иметь различную форму, размеры и соотношение сторон. На основании этих характеристик можно выделить несколько видов объемных прямоугольников, которые часто используются в математике и инженерных расчетах.

• Куб — это объемный прямоугольник, у которого все стороны равны между собой.
• Квадратный параллелепипед — это прямоугольный параллелепипед, у которого две пары смежных сторон равны между собой.
• Прямоугольный параллелепипед — это прямоугольный объемный прямоугольник любых размеров и пропорций.

Одним из важных понятий, связанных с объемными прямоугольниками, является их объем. Объемный прямоугольник можно выразить через длину, ширину и высоту, используя формулу: объем = длина x ширина x высота. Также можно использовать площадь одной из граней и высоту, чтобы найти объем: объем = площадь грани x высота.

Общая характеристика

Предметы в геометрическом изображении состоят из отдельных частей: точек, линий, лучей, отрезков и вершин. Отдельно взятый предмет имеет свое предназначение.

Основные понятия о составляющих

Когда все точки фигуры принадлежат одной плоскости, она является плоской. К ней относятся отрезок, прямоугольник. Существуют геометрические объекты, не являющиеся разновидностью плоскости, — куб, шар, пирамида, призма.

Минимальным объектом геометрии является точка. Определение того, какой она должна быть известно из школьного математического курса. Учебник характеризует ее как объект, не имеющий измерительных особенностей. Точка (Т) не содержит стандартных свойств: высоты, длины, радиуса, важным является только ее расположение. Обозначается числом или большой заглавной буквой. Например, точка называется D, E, F или 1, 2, 3. Несколько точек бывают отмечены разными цветами или буквами для удобного различия.

Линия состоит из множества точек. Измеряется длина этого составляющего объекта и обозначается маленькими буквами (abc).

Виды линий:

• Замкнутая. Когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.
• Разомкнутая. Начало и окончание не соединяются.
• Прямая. Обозначается буквой а или b.
• Ломаная. Заключается в соединенных отрезках не под углом 180 градусов. Линия обозначается перечислением всех вершин.
• Кривая.Отличная от прямой линии.

Существуют подвиды прямой линии: пересекающиеся, содержащие общую точку и когда две прямые линии соединяются в одной точке.

Луч в математике представляет часть прямой, имеющей начальную точку, но не имеющую конец. Это продолжение в одну сторону. Если Т разделяет линию пополам — получается два луча. Лучевые линии совпадают, когда расположены на одной прямой, начинаются в точке или направляются в одну сторону.

Отрезок представляет составную часть прямой, ограниченной двумя точками — она имеет начало и конец, поэтому измеряется. Длина отрезка представляет расстояние между его первой и последней точками. Через одну Т проводится бесконечное число линий, а через две — кривые и только одна прямая.

Стандартные объекты

К основным фигурам геометрии на плоскости относятся прямоугольник, треугольник, квадрат, многоугольник и круг. Прямоугольник выглядит как фигура, состоящая из четырех сторон и четырех прямых углов (ПУ). Противоположные стороны равны между собой. В математике прямоугольник обозначается четырьмя латинским заглавными буквами. Все ПУ расположены под 90 градусов. Прямоугольник с равными, одинаковыми сторонами называется квадратом.

Фигура, имеющая 3 стороны и столько же углов (вершин), называется треугольником. Существует классификация этой фигуры по типу У.

Виды треугольника в зависимости от угла (У):

• Прямой. Один У будет прямым, два — менее 90 градусов.
• Острый. Градусная мера больше 0, но меньше 90 гр.
• Тупой. Один У тупой, два других будут острыми.

Радиус круга — промежуток от середины окружности до любой ее точки. Диаметр — это отрезок, соединяющий две точки окружности, проходящий через ее середину.

Параллелепипед — это призма, у которой основанием является параллелограмм. Когда все ребра параллелепипеда равны, получается куб.

Многогранная фигура, у которой одна грань является многоугольником, а остальные грани (боковые) — треугольники с общей вершиной, называется пирамидой.

Семиугольник (гептагон) — это многоугольник с 7 углами. Многоугольник представляет замкнутую ломанную линию.

Основные фигуры перечислены, но геометрия включает еще сложные объекты, использующиеся в различных областях жизни.

Основные аспекты применения объемных прямоугольников в строительстве

Объемные прямоугольники широко используются в строительстве благодаря своей простоте и универсальности. Они представляют собой трехмерную фигуру, состоящую из шести прямоугольных граней. В строительстве объемные прямоугольники применяются для создания основных элементов зданий, таких как стены, потолки и полы.

Основными преимуществами использования объемных прямоугольников в строительстве являются:

• Простота конструкции. Объемные прямоугольники не требуют сложных математических расчетов и специальных навыков для их создания и монтажа.
• Универсальность. Объемные прямоугольники могут быть использованы для строительства различных видов зданий, начиная от жилых домов и заканчивая промышленными сооружениями.
• Прочность. Благодаря своей конструкции из прямоугольных граней, объемные прямоугольники обладают высокой прочностью и устойчивостью к различным нагрузкам.
• Эффективность. Использование объемных прямоугольников позволяет сэкономить время и ресурсы при строительстве, так как они легко монтируются и не требуют дополнительной обработки или отделки.

Использование объемных прямоугольников в строительстве позволяет более эффективно использовать пространство, обеспечивая максимальную функциональность и комфорт в зданиях. Они широко применяются как в строительстве новых зданий, так и в реконструкции и ремонте существующих помещений.

Однако, необходимо учитывать, что для правильного использования объемных прямоугольников в строительстве требуется соответствующий проект и компетентный подход к их размещению и сборке. Кроме того, необходимо учитывать все строительные нормы и стандарты, чтобы обеспечить безопасность и долговечность создаваемой конструкции.

Объемные геометрические фигуры

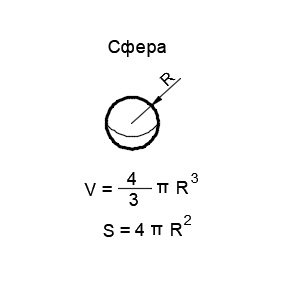
Шар — это геометрическое тело, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой шара является его радиус.

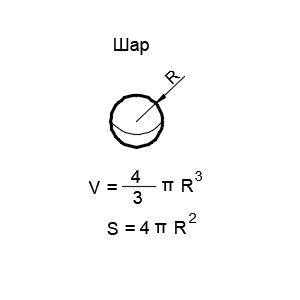
Сфера — это оболочка геометрического тела, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой сферы является её радиус.

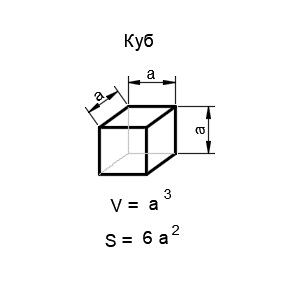
Куб — это геометрическое тело, представляющее собой правильный многогранник, каждая грань которого представляет собой квадрат. Основной математической характеристикой куба является длина его ребра.

4. Параллелепипед

Параллелепипед — это геометрическое тело, представляющее собой многогранник, у которого шесть граней и каждая из них прямоугольник. Основными математическими характеристиками параллелепипеда являются длины его ребер.

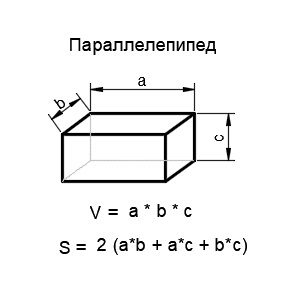
5. Призма

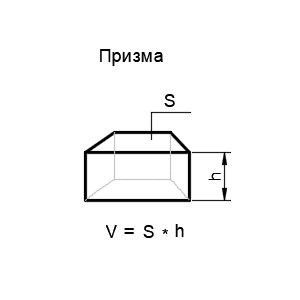
Призма — это многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани параллелограммами, имеющими общие стороны с этими многоугольниками. Основными математическими характеристиками призмы являются площадь основания и высота.

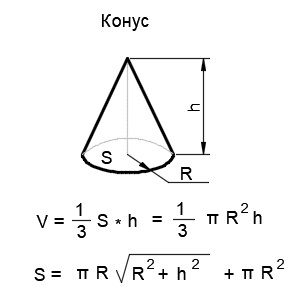
Конус — это геометрическая фигура, полученная объединением всех лучей, исходящих из одной вершины конуса и проходящих через плоскую поверхность. Основными математическими характеристиками конуса являются радиус основания и высота.

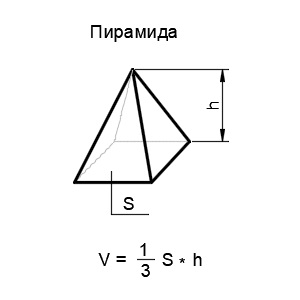
7. Пирамида

Пирамида — это многогранник, основанием которого является произвольный многоугольник, а боковые грани являются треугольниками, имеющие общую вершину. Основными математическими характеристиками пирамиды являются площадь основания и высота.

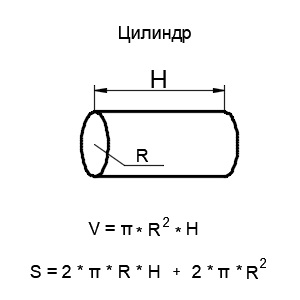
8. Цилиндр

Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Основными математическими характеристиками цилиндра являются радиус основания и высота.

Быстро выполнить эти простейшие математические операции можно с помощью наших онлайн программ. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлены все геометрические фигуры, которые наиболее часто встречаются в геометрии для представления объекта или его части на плоскости или в пространстве.

Существует бесконечное множество форм. Формой называют внешнее очертание предмета.

Изучение форм можно начинать с самого раннего детства, обращая внимание своего ребенка на окружающий нас мир, который состоит из фигур (тарелка – круглая, телевизор – прямоугольный). Уже с двух лет малыш должен знать три простые фигуры – круг, квадрат, треугольник.
Сначала он их должен просто показывать, когда вы это просите

А в три года уже называть их самостоятельно и отличать круг от овала, квадрат от прямоугольника

Уже с двух лет малыш должен знать три простые фигуры – круг, квадрат, треугольник.
Сначала он их должен просто показывать, когда вы это просите. А в три года уже называть их самостоятельно и отличать круг от овала, квадрат от прямоугольника.

Чем больше упражнений на закрепление форм будет выполнено ребенком, тем больше новых фигур он запомнит.

Будущий первоклашка должен знать все простые геометрические фигуры и уметь составлять из них аппликации.

Что такое точка?

Как только маленький ребенок берет в ручки карандаш, он уже замечательно умеет рисовать геометрическую фигуру. Какую? – удивитесь вы. Это точка.

Точка – наименьшая, простейшая фигура геометрии, никак не измеряется.

 И строить её умеет даже маленький ребенок.

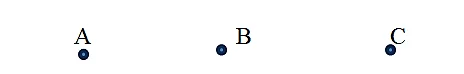
Обозначать точки в математике, принято большими буквами латиницы.

Произносится:точка А, точка В, точка С.

Следующее понятие, которое мы рассмотрим, знакомо каждому с самого детства. Нет ничего проще, чем нарисовать прямую линию. Многие успешно рисовали их на новых обоях, мебели. А оказывается – она одна из основных фигур геометрии.