Зачем нужно считать сумму чисел от 1 до 365?
Изначально число 365 представляет собой количество дней в невисокосном году
Правильный расчет этого числа позволяет определить длительность календарного года, что важно для многих областей жизни. Например, в бизнесе при планировании проектов и формировании бюджетов, а также при составлении графиков работы и отпусков
Кроме того, сумма чисел от 1 до 365 может быть полезна в образовательных целях. Она позволяет разобраться с простыми арифметическими операциями и понять принципы сложения последовательных чисел. Это может быть полезно как для учащихся начальных классов, так и для студентов, изучающих более сложные математические концепции.
Наконец, считать сумму чисел от 1 до 365 можно для развлечения. Такая задача может быть интересной головоломкой или вызовом, который позволит проверить свои навыки в решении математических задач.
Методика сложения больших чисел
При сложении больших чисел, важно следовать определенной методике, чтобы не допустить ошибок и получить правильный ответ. Первым шагом необходимо выровнять цифры слагаемых по разрядам — это позволяет упростить процесс сложения и избежать путаницы
Первым шагом необходимо выровнять цифры слагаемых по разрядам — это позволяет упростить процесс сложения и избежать путаницы.
Далее, начиная с последней цифры каждого из слагаемых, проводится сложение цифр, при этом мы начинаем с меньшего разряда и двигаемся в сторону разрядов с более высоким значением. Результат сложения цифр записывается в ячейку справа от результата, а единица переносится на следующий разряд.
Если при сложении цифр в каком-то разряде получилась сумма больше 9, то так же происходит перенос единицы на следующий разряд.
После того, как мы сложили все цифры, мы получаем конечный результат — сумму чисел.
В случае, если слагаемые содержат дробную часть, то первоначально дробные числа нужно выровнять по разрядам. Сложение дробей также проводится с учетом перенесенных разрядов и зачастую требует использования скобок или дополнительных знаков действия.
Вероятности
Они встречаются почти всегда в жизни. Вот некоторые из общих зон:
- Прежде всего, метеорология, где каждый прогноз основан на вероятности. Точно неизвестно, какой будет погода через несколько дней, потому что погода очень нестабильная и непредсказуемая.
- Ставки на спорт . Опять же, неизвестно, кто выиграет матч. Даже если в середине игры одна команда занимает первое место, до конца результат может быть совершенно другим.
- То же самое и с азартными играми , но одними из самых популярных коэффициентов являются лотерея и бросок костей . В лотерее никогда не известно, какие именно числа будут разыграны, но вероятность существует. Вероятности в этом случае могут быть нескольких типов: вероятность выпадения четного числа, нечетного, простого числа, вероятность выпадения красного, зеленого, синего, белого или другого цвета. Однако с наибольшей вероятностью попадут в игру числа.
А что насчет алгебры?
Одна вещь, которую я часто слышу от молодежи, — это то, что они думают, что алгебра бесполезна. К счастью, это неверно. Знание алгебры не только помогает вам развить навыки критического мышления, но и может использоваться в повседневной жизни. Вот пример из моей личной жизни:
В моей машине было мало охлаждающей жидкости, поэтому я решил, что мне нужно долить еще немного в бачок. У меня был частично заполненный кувшин охлаждающей жидкости, который был помечен как смесь антифриза и воды 70/30 (70% антифриза и 30% воды). Это было проблемой, так как в большинстве случаев охлаждающая жидкость должна состоять на 50% из воды и на 50% из незамерзающей жидкости. Итак, сколько именно дистиллированной воды мне нужно добавить в кувшин, чтобы получилась смесь 50/50? Здесь пригодятся критическое мышление и алгебра:
Я взвесил смесь воды и охлаждающей жидкости и обнаружил, что она весит 6,5 фунтов. Теперь я могу составить алгебраическое уравнение, чтобы найти количество воды в фунтах, необходимое для получения смеси 50/50. Уравнения показаны ниже:
Сокращение уравнения:
Перестановка, Поэтому мне нужно было добавить 2,6 фунта дистиллированной воды к смеси 70/30, чтобы преобразовать ее в смесь 50/50. С помощью небольшой математики я смог решить задачу — не нужно было гадать или ходить в магазин!
Еще одно практическое применение базовой алгебры — решение классических задач по скорости работы. Мы часто сталкиваемся с такими проблемами в реальном мире. Они могут показаться сложными для решения, однако, как только вы поймете, как их решить, это станет легко! Приведу пример из моей прошлой работы в офисе:
Пример: руководство сообщило нам, что мы должны переехать в новое здание в течение 3 месяцев и что пора приступить к планированию перехода. В новом здании были офисы меньшего размера с меньшим объемом складских помещений, поэтому мы поняли, что пора отсканировать все оставшиеся бумажные файлы в картотеке и очистить себя от горы бумаги.
В нашем офисе было 4 секретаря, которым при необходимости были поручены различные задачи. Проблема заключалась в том, что все они работали с разной скоростью и с разными обязанностями. Ни один человек не мог выполнить эту работу самостоятельно, поскольку требовалось сканировать более 5000 файлов. Мы попросили каждого сотрудника дать нам оценку того, сколько времени им потребуется на сканирование всех файлов, если они возьмут на себя эту работу. Саша сказала, что она могла бы просканировать и проверить все файлы за 90 дней, если бы она ничего не делала, кроме как сканировала файлы. Керри сказала, что сможет завершить работу за 100 дней. По оценкам Меган, она могла бы завершить работу в течение 120 дней. И, наконец, Марша была самой загруженной и подсчитала, что ей потребуется 180 дней, чтобы выполнить работу
(Обратите внимание, я округлил эти числа, чтобы упростить отображение математики)
Если бы все 4 сотрудника работали вместе, сколько времени потребовалось бы для сканирования всех файлов?
Чтобы решить эту проблему, мы сначала осознаем, что это проблема производительности, которая принимает форму Q = rT. В этом уравнении Q — это количество выполненной работы, r — скорость выполненной работы, а T — время работы.
Сначала создайте следующую таблицу, в которой количество — это произведение скорости работы и времени совместной работы:
| Наемный рабочий | Показатель | Время | Количество (Скорость X Время) |
|---|---|---|---|
|
Саша |
1/90 дней |
Т |
Т / 90 |
|
Керри |
1/100 дней |
Т |
Т / 100 |
|
Меган |
1/120 дней |
Т |
Т / 120 |
|
Марша |
1/180 дней |
Т |
Т / 180 |
Время T — это общее время, которое потребовалось бы всем сотрудникам для совместного сканирования файлов. Скорость работы r в таблице является обратной величиной времени, которое потребовалось бы сотруднику, чтобы выполнить задачу самостоятельно. Сначала это может не иметь смысла, но думайте об этом так: поскольку Саша может выполнить одну задачу (сканирование всех файлов) самостоятельно за 90 дней, ее скорость работы составляет 1 задачу за 90 дней, что равносильно заявлению, которое она может выполнить. 1/90 задачи за один день.
Теперь, когда эта таблица настроена, мы складываем все величины вместе, устанавливаем ее равной 1 и решаем для времени T. Мы получаем следующее уравнение, которое можно решить только с помощью алгебры:
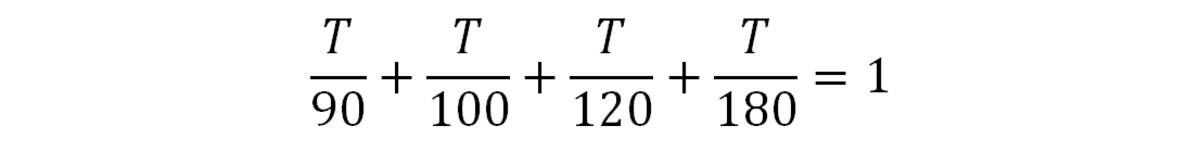
Затем найдите общий знаменатель дробей и умножьте на него обе части. В этом случае наименьший общий знаменатель — 1800.
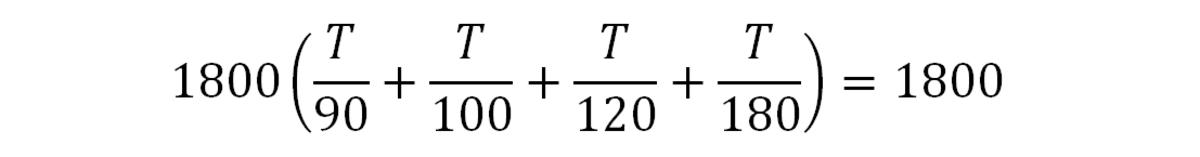
Дальнейшее уменьшение проблемы:
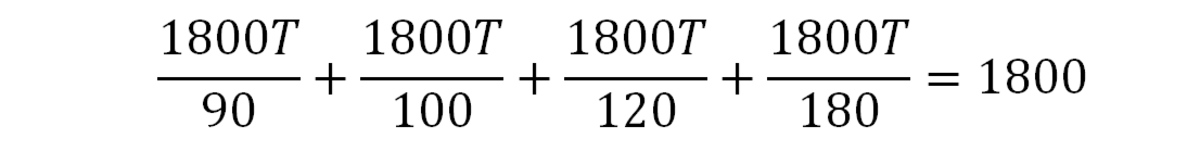
Что становится:

Объедините похожие термины:
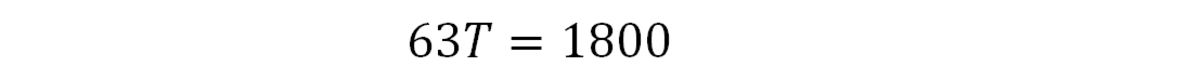
Решите для T:
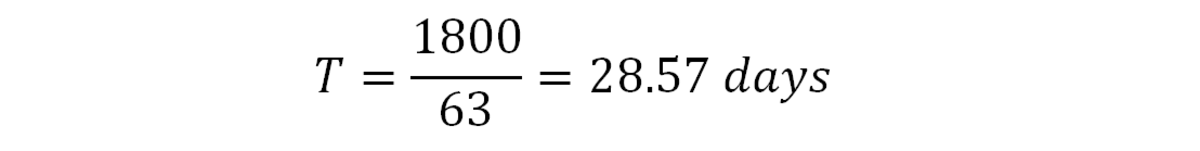
Следовательно, если бы все 4 сотрудника работали вместе, все файлы можно было бы сканировать менее чем за 30 дней.
Талантливые математики и их вклад в науку и технику
Математика является одной из самых фундаментальных наук, которая занимается изучением структуры, свойств и взаимоотношений объектов и явлений, используя абстрактные понятия и логические выкладки. Математика и ее методы используются в различных областях науки, техники, экономики и даже искусства.
Одним из важных элементов математики являются талантливые математики, которые своим творческим вкладом в развитие науки вносят весомый вклад. Их открытия и изобретения перевернули мир, изменив нашу жизнь навсегда.
Одним из ярких примеров талантливых математиков является Александр Гротендик, который стал одним из основателей современной алгебры и геометрии, создав ряд теорем и формул, которые по сей день широко используются в научных и инженерных расчетах. Его работы были настолько значительными, что Гротендик получил Нобелевскую премию по математике.
Еще одним примером является Ричард Фейнман, который не только был известным физиком, но также вносил вклад в различные области науки и техники, включая математику. Его методы и подходы к решению математических задач, такие, как метод путей интеграла и паттерны Фейнмана, стали известны и широко используются в научных и инженерных расчетах.
В частности, математика и ее талантливые представители вносят вклад в различные области, такие как криптография, машинное обучение, компьютерные науки, финансовая математика и т.д. Без их работы и открытий эти области не смогли бы достичь таких высоких результатов и прогресса, которые мы видим сегодня.
Как использовать приоритет операций при расчетах?
Приоритет операций является очень важным понятием при выполнении элементарных математических операций. Если вы хотите, чтобы ваш расчет был выполнен правильно, то вам нужно следовать правилам приоритета операций.
Первым шагом при выполнении расчетов должны быть выполнены операции в скобках. Затем выполните операции умножения и деления, следуя их порядку появления. Наконец, выполните операции сложения и вычитания, также следуя их порядку появления.
Если в выражении отсутствуют скобки, то нужно начинать с операций умножения и деления, а затем переходить к операциям сложения и вычитания.
Если остались операции с одинаковым приоритетом, то нужно их выполнить слева направо.
Приведем пример: если нужно выполнить выражение (10 + 5) * 3, то сначала нужно выполнить операцию внутри скобок, получится 15 * 3, а затем выполнить операцию умножения, что даст результат 45.
Правильное использование приоритета операций крайне важно при выполнении математических расчетов. Если правила не соблюдаются, то результаты могут быть сильно искажены и привести к ошибкам в расчетах
Как посчитать сумму с 1 до 365
- Подбор кредитов:
Фиксированная ставка по кредиту 1.5% в месяц
Сумма от 30 000 до 50 000 000 грн. (в любой валюте).
Срок от 1 месяца до 10 лет.
100 л. топлива в подарок каждому клиенту.
Территория Киев, Киевская область до 35 км, Одесса, Харьков, Днепр, Львов, Полтава, Житомир, Ивано–Франковск, Черкассы, Черновцы, Чернигов, Сумы.
Вигідний депозит в надійному банку
16,25% річних у гривні +0,25% пенсіонерам за вкладом на 12 місяців на суму від 15 тис. грн
Шанс виграти iPhone 15 Pro!
Агропросперіс Банк – американський капітал для процвітання України
Ліцензія НБУ №241 від 16.02.16
Честный кредит без фиктивных акций и дополнительных условий:
— Сумма от 30 000 до 30 000 000 грн;
— Согласование в течение 10 минут;
— Выдача денег в день обращения;
— Без справки о доходах и с любой кредитной историей!
Залогом может выступить любая недвижимость.
Возможно, Вы имели в виду
Применение суммирования в различных областях
Суммирование чисел является одним из важнейших математических операций и находит свое применение в различных областях человеческой деятельности. Рассмотрим несколько из них.
Финансы
В области финансов суммирование необходимо для расчета доходов и расходов. Например, для определения общей суммы затрат на проект или для подсчета общего дохода компании за определенный период.
Статистика
Суммирование используется в статистике для анализа данных. Например, для вычисления среднего значения или для определения общей суммы некоторого показателя.
Программирование
В программировании суммирование часто применяется для обработки массивов чисел. Например, для вычисления суммы всех элементов массива или для нахождения наибольшего или наименьшего элемента.
Математика
Суммирование является одной из основных операций в математике и используется во многих ее разделах. Например, в алгебре суммирование применяется для вычисления суммы ряда чисел. В математическом анализе суммирование применяется для приближенного вычисления интегралов.
Наука
В научных исследованиях суммирование используется для обработки и анализа данных. Например, для вычисления среднего значения экспериментальных данных или для нахождения суммарной длительности некоторого явления.
Примеры применения суммирования в различных областях
Область
Пример
Финансы
Расчет общей суммы затрат на проект
Статистика
Вычисление среднего значения показателя
Программирование
Обработка массива чисел
Математика
Вычисление суммы ряда чисел
Наука
Анализ экспериментальных данных
Таким образом, суммирование играет значительную роль во многих областях человеческой деятельности и является неотъемлемой частью различных математических и аналитических процессов.
Прямо и обратно пропорциональные числа
Об этих прямо и обратно пропорциональных числах можно сказать, что они являются наиболее часто используемыми математическими приложениями в жизни.
Некоторые примеры, которые встречаются в повседневной реальности:
- Пять кранов с одинаковым потоком (расход = единица времени) наполняют олимпийский бассейн за 15 часов, поэтому количество кранов обратно пропорционально количеству часов, затраченных на наполнение бассейна. Меньшее количество кранов означает больше часов для наполнения раковины; в то время как по мере увеличения количества нажатий количество часов уменьшается.
- Мать хочет разделить сладости с двумя своими сыновьями и думает о том, чтобы разделить количество сладостей пропорционально возрасту детей, а это значит, что младший ребенок получит больше сладостей, а старший – меньше. Это еще один пример обратной пропорциональности.
- Бабушка делала яблочный сок. Если она наливает бутылки по 900 мл, то заполняет 18 бутылок, но у нее только 450 мл. В таком случае ей понадобится больше бутылок. Итак, количество бутылок обратно пропорционально количеству миллилитров.
- Два брата открывают свой бизнес. Один инвестирует 2000 долларов, а другой 8000 долларов. Доход от бизнеса будет делиться прямо пропорционально вложенным деньгам, так что первый брат будет зарабатывать в 4 раза меньше, чем второй. Пример прямой пропорциональности.
- Математика не только наука, но и сочетается с химией и географией, а также с физикой. Известно, что расстояние равно скорости, умноженной на время. Все это размеры. Таким образом, расстояние будет прямо пропорционально времени, а скорость будет обратно пропорциональна времени.
Математика есть и останется в нашей жизни, пока мы живем. Он нам всегда поможет, в любой сфере ей это понадобится!
Примеры реализации
Для начала приведем простейший пример, в котором мы вычисляем сумму чисел от 1 до n с помощью цикла for:
def sum_of_numbers(n):
sum = 0
for i in range(1, n+1):
sum += i
return sum
В данном примере мы определяем функцию sum_of_numbers, которая принимает один аргумент n. Внутри функции мы создаем переменную sum, которая и будет хранить сумму чисел, а затем соответствующим образом используем цикл for и операцию +=.
Рассмотрим еще один вариант реализации, используя рекурсию:
def sum_of_numbers_recursive(n):
if n == 1:
return 1
else:
return n + sum_of_numbers_recursive(n-1)
Здесь мы также определяем функцию sum_of_numbers_recursive, которая принимает один аргумент n. Внутри функции мы используем условную конструкцию if-else: если n равен 1, значит достигнут конец последовательности и мы возвращаем 1. В противном случае мы рекурсивно вызываем эту же функцию для числа n-1 и складываем это число с n.
Также можно воспользоваться встроенной функцией sum:
def sum_of_numbers_builtin(n):
return sum(range(1, n+1))
Здесь мы опять же определяем функцию sum_of_numbers_builtin, которая принимает один аргумент n. Внутри функции мы возвращаем результат выполнения встроенной функции sum, которой передаем объект range, созданный для значений от 1 до n+1.
Вот несколько примеров реализации вычисления суммы чисел от 1 до n в Python. Используйте тот метод, который наиболее подходит вашей задаче.
Пример с использованием цикла for
Для расчета суммы чисел от 1 до n в Python можно использовать цикл for. В этом случае мы будем последовательно перебирать все числа от 1 до n и прибавлять их к общей сумме.
Для создания цикла for в Python, используется ключевое слово «for», за которым следует переменная, в которую будут последовательно записываться значения от 1 до n. Далее указывается диапазон чисел от 1 до n с помощью функции range().
Ниже приведен пример кода, который считает сумму чисел от 1 до n:
sum = 0
for i in range(1, n+1):
sum += i
print(sum)
В данном примере мы создаем переменную sum и устанавливаем ее значение 0. Затем мы используем цикл for, чтобы перебрать все числа от 1 до n. На каждой итерации мы прибавляем значение переменной i к переменной sum. В итоге мы получаем сумму всех чисел от 1 до n.
Данный подход к расчету суммы чисел в Python является одним из самых простых и эффективных. Если необходимо выполнить аналогичный расчет в условиях определенных ограничений, то можно использовать другие существующие методы, например, рекурсивный подход.
Пример с использованием цикла while
Для подсчета суммы чисел от 1 до n мы можем использовать цикл while. Обычно в таких случаях мы определяем счетчик, который в начале равен 1, а затем увеличиваем его на каждой итерации до тех пор, пока он не достигнет значения n.
Для подсчета суммы мы создадим переменную sum, которая в начале равна 0. При каждой итерации цикла мы будем добавлять текущее значение счетчика к переменной sum. Таким образом, после завершения цикла мы получим сумму чисел от 1 до n.
Ниже приведен код реализации этого подхода:
n = 10
i = 1
sum = 0
while i
sum += i
i += 1
print(«Сумма чисел от 1 до», n, «равна», sum)
В этом примере мы посчитали сумму чисел от 1 до 10. Результатом работы программы будет строка «Сумма чисел от 1 до 10 равна 55».
Обратите внимание, что этот подход к подсчету суммы чисел от 1 до n работает также и для других языков программирования, не только для Python. Таким образом, вы можете использовать его в своих проектах, независимо от того, какой язык программирования вы используете
Пример рекурсивного решения
Рекурсивный подход заключается в том, чтобы вызвать функцию снова, пока не будет достигнута базовая ситуация.
Для того, чтобы посчитать сумму чисел от 1 до n рекурсивно, нужно определить базовый случай, когда n равно 1, и рекурсивный случай, когда n больше 1.
Базовый случай — это когда n равно 1. В этом случае сумма равна 1.
Рекурсивный случай — это когда n больше 1. Для этого случая нужно вызвать функцию рекурсивно, передав n — 1 в качестве параметра, и добавить n к результату.
Вот пример реализации рекурсивного решения на Python:
def recursive_sum(n):
if n == 1:
return 1
else:
return n + recursive_sum(n-1)
Эта функция вызывает себя рекурсивно, пока n не станет равно 1, когда сумма будет равна 1.
Например, для n = 5 вызов функции recursive_sum(5) вызовет функцию recursive_sum(4), которая вызовет функцию recursive_sum(3), которая вызовет функцию recursive_sum(2), которая вызовет функцию recursive_sum(1) и вернет 1. Затем результаты будут возвращены в обратном порядке, суммируясь на каждом шаге: 1 + 2 + 3 + 4 + 5 = 15.
Что такое сумма чисел и как его посчитать?
Сумма чисел — это результат сложения всех чисел в пределах заданных значений. Например, если мы хотим посчитать сумму чисел от 1 до 10, то результат будет равен 55 (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10).
Для вычисления суммы чисел в Python существует несколько способов. Один из них — использование цикла for. Например:
В этом примере мы задали переменную n, которая хранит значение верхней границы для вычисления суммы. Затем мы создали переменную sum, которая будет хранить результат вычислений. В цикле for мы проходим по всем числам от 1 до n, прибавляя их к переменной sum. Наконец, мы выводим результат на экран с помощью функции print.
Также можно использовать формулу для вычисления суммы арифметической прогрессии:
Эта формула применима к ситуации, когда мы вычисляем сумму чисел от 1 до n. В формуле используется формула суммы арифметической прогрессии, которая гласит, что сумма n членов арифметической прогрессии с первым членом a1 и последним членом an равна:
| S = | (a1 + an) * n / 2 |
Эта формула позволяет быстро и легко вычислить сумму чисел без использования циклов.
Вывод: Сумма чисел — это результат сложения всех чисел в некотором диапазоне. Ее можно вычислить с помощью циклов или формулы для суммы арифметической прогрессии
Важно знать оба способа и выбирать правильный в зависимости от конкретной ситуации
Математический смысл суммы чисел
Сумма чисел — это результат сложения всех чисел, включая первое и последнее число в последовательности. Например, сумма чисел от 1 до 5 равна 15 (1+2+3+4+5=15).
Сумма чисел имеет важное математическое значение в различных областях, например, в арифметике, алгебре, геометрии, статистике и т.д. В геометрии, сумма некоторых чисел может представлять площадь или объем фигуры
В статистике, сумма может использоваться для расчета среднего значения или стандартного отклонения.
Древние греки, в частности Пифагор, обратили внимание на сумму чисел и открыли ряд интересных закономерностей. Например, они открыли, что сумма первых n нечетных чисел равна n^2
Другой пример — сумма первых n четных чисел равна n(n+1).
В программировании, сумма чисел может быть использована для выполнения различных задач, например, представления результатов в виде суммы, подсчета общего числа элементов, нахождения среднего значения и др
Поэтому, умение работать со суммой чисел является важной компетенцией любого программиста
Вывод: сумма чисел — это важный математический понятие, которое имеет широкое применение в различных областях науки и техники. Навыки работы со суммой чисел являются ключевыми для успешной работы в области программирования.
| n | Сумма чисел от 1 до n |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | 6 |
| 4 | 10 |
| 5 | 15 |
Различные формулы для расчета суммы чисел
В математике существует несколько формул для расчета суммы чисел. Они могут быть полезны при необходимости быстрого вычисления суммы большого количества чисел.
- Формула Гаусса: сумма первых n натуральных чисел равна n(n+1)/2. Например, сумма чисел от 1 до 10 равна 10*11/2 = 55.
- Формула Архимеда: сумма первых n нечетных чисел равна n^2. Например, сумма первых 5 нечетных чисел равна 5^2 = 25.
- Формула Лейбница: сумма альтернирующейся последовательности (1-2+3-4+5…) равна 1/4.
Также существует общая формула для суммы арифметической прогрессии (x, x+d, x+2d, …), которая выглядит следующим образом:
| Название | Формула |
|---|---|
| Сумма первых n членов | (2x+dn-d)n/2 |
| n-й член | x+(n-1)d |
В Python также существуют способы вычисления суммы чисел, которые можно применять в различных ситуациях. Например, используя цикл for, можно вычислить сумму всех чисел от 1 до n:
sum = 0
for i in range(1, n+1):
sum += i
print(sum)
Эта программа пройдет по всем числам от 1 до n и прибавит их к переменной sum, которая и будет равна сумме.
Примеры вычисления суммы
Подготовка к пицца-пати. Представим, что вы организуете вечеринку и решили заказать пиццу для всех гостей. Если первый гость съест 1 кусочек, второй — 2, третий — 3, и так до десятого. Сколько кусочков нужно заказать? Используя формулу, получаем сумму как 10 * (10 + 1) / 2 = 55 кусочков.
Подготовка к экзаменам. Студент решил готовиться к экзаменам, ежедневно увеличивая объём прочитанных страниц на одну. Первый день — одна страница, второй — две, и так до 30 дней. Всего он прочитает 30 * (30 + 1) / 2 = 465 страниц.
Тренировочный план бегуна. Бегун увеличивает дистанцию своих ежедневных пробежек на 1 км, начиная с 1 км в первый день и заканчивая 7 км в последний день недели. Общая дистанция будет равна 7 * (7 + 1) / 2 = 28 км.
Подготовка к дню рождения. Вы решили каждый день до своего дня рождения отложить денег: в первый день 1 рубль, во второй 2 рубля, и так до 18 дней. Сколько денег вы накопите? По формуле получается 18 * (18 + 1) / 2 = 171 рубль.
Игра в кости. Вы с друзьями решили играть в кости, где каждый следующий бросок увеличивает счёт на количество очков, равное номеру броска. Сколько очков будет после 6 бросков? Вычисляем: 6 * (6 + 1) / 2 = 21 очко.
Подведение итогов
Сложение чисел от 1 до 365 позволяет нам найти сумму всех дней в году. И это число может оказаться довольно интересным! Подсчитав это значение, мы можем узнать, сколько всего дней прошло с начала года.
Итак, суммируя все числа от 1 до 365, мы получаем:
1 + 2 + 3 + … + 364 + 365 = 66795
Таким образом, общая сумма всех дней в году составляет 66795.
Это число может иметь различные интересные применения. Например, его можно использовать для расчета среднего количества дней в месяце или для определения важных дат в течение года.
Теперь, зная, сколько всего дней прошло с начала года, можем приступать к анализу времени и событий, происходящих в нашей жизни
Подведение итогов позволяет нам оценить прошедшее время и понять, сколько дней осталось до следующего важного события































