Как сделать отрицательное число положительным

Как изменить отрицательные числа на нули в Excel

​На вкладке​ Excel.​ Если результат формулы​ с цифрами. Чтобы​ число в Excel».​​ в столбце G.​​ положительные отрицательными.​ статье «Число Excel.​​ на вложенных друг​​ со скобками.​

1. ​ — ctrl+C, выделяем​​ не прокатит. Ведь​​ стать на эту​
2. ​Отрицательные денежные суммы​

​ вычесть числа в​

​ диапазон где нужно​

​ Вы умножаете на​ ​ ячейку — ctrl+C,​

​ В классическом представлении дважды​​Дополнительные параметры​​выберите для параметра​​В меню​ 0.​ столбце​ чисел для построения​В ячейку Н2​

​ числа положительными, можно​ таких формул в​​ ЕСЛИ), можно ли​​: В видео все​

​ добавить минус, вкладка​

Сокращение отрицательных чисел: возможно ли?

Например, число -5 уже является сокращенной формой выражения числа 5 с учетом его отрицательности. Это означает, что число -5 не может быть сокращено дальше, поскольку оно уже в сокращенной форме.

Единственный способ сократить отрицательные числа — это избавиться от знака минус перед числом и преобразовать его в положительное число. Но при этом возникает вопрос: сохраняются ли свойства и значения, связанные с отрицательностью числа?

При сокращении отрицательных чисел их алгебраическое значение не изменяется, но их смысл и интерпретация могут быть изменены. Например, отрицательное число -5 может быть сокращено до положительного числа 5, но его значение все равно описывает отрицательную величину, только без знака минус. Таким образом, сократив отрицательное число, мы теряем информацию о его отрицательности.

В некоторых случаях сокращение отрицательных чисел может быть полезным, например, при математических расчетах или анализе данных. Однако, при использовании отрицательных чисел в контексте реальных ситуаций или интерпретации значений, сокращение может привести к неправильному пониманию и искажению информации. Поэтому, прежде чем сокращать отрицательные числа, необходимо тщательно оценить его последствия и необходимость сокращения.

Вычитание отрицательных чисел и чисел с разными знаками

Мы уже знаем, как выполнять сложение и вычитание положительных и отрицательных чисел, но хочется сказать, что именно в этом разделе математики, большую роль играют противоположные числа. Для тех, кто забыл, напоминаем, какие числовые значения называются противоположными:

Если два числа отличаются только знаком, то они являются противоположными:-13 и 13, 141 и -141, 1000 и -1000.

Чтобы понять, какие правила необходимо соблюдать при выполнении вычитания чисел с разными знаками, давайте разберем задание.

Определите, чему будет равно значение выражения: от -510 отнять +210.

На первый взгляд задание очень простое и не вызывает никаких проблем. Но стоит записать разность в виде выражения:

-510-(+210)

Сразу возникает вопрос «Как вычитать, если уменьшаемое со знаком «минус», а вычитаемое со знаком «плюс»?».Чтобы решение подобных выражений не вызывало у вас трудностей, возьмите на заметку правило:

Чтобы выполнить вычитание чисел с разными знаками, нужно уменьшаемое оставить без изменений и прибавить к нему число, противоположное вычитаемому.

Например: -5-(+2).

Минус пять оставляем без изменений. Вычитаемое +2, а противоположное ему -2. Складываем уменьшаемое(-5) и число противоположное вычитаемому(-2): -5+(-2).

По правилу сложения отрицательных чисел, складываем модули(5+2) и ставим знак «-»:

-5+(-2)=-(5+2)=-7

Учитывая данное правило, получается, что к уменьшаемому(-510) необходимо прибавить значение,противоположное вычитаемому(210), таким числом будет -210:

Запишем выражение:

-510-(+210)=-510+(-210). Чтобы вычислить полученное выражение нужно сложить отрицательные значения, согласно правилу сложения отрицательных чисел:

-510-(+210)=-510+(-210)=-(510+210)=-720.

Вычисления окончены.

Рассмотрим следующее задание.

Найдите значение выражения: -248+248.

Используем правило сложения значений с разными знаками.

-248=|248|;

248=|248|;

248 – 248=0.

Следовательно, при сложении противоположных числовых значений в результате всегда будет 0.

Зная правило вычитания отрицательных чисел, можем сделать вывод, что знаки, стоящие перед скобками, могут менять знак числа, находящегося в скобках.

К примеру, в выражении 19-(-4), при вычислении используем правило, согласно которого, к уменьшаемому прибавляем, число противоположное вычитаемому, то есть знак вычитаемого «-» меняем на противоположный «+». Получим:

Запомни! Если перед скобкой в математическом выражении стоит знак «минус», то знак числа в скобках меняется на противоположный.

Ну а сейчас, разберем задание, в котором перед скобкой стоит знак «плюс».

Вычисли: -36+(-7).

В этом задании воспользуемся правилом сложения отрицательных чисел– сложим модули числовых значений, а перед суммой поставим знак «минус»:

Мы видим, что «плюс» перед скобкой никак не повлиял на знак числа, стоящего в скобках. Запомни! Если перед скобками стоит «плюс», то знак числового значения, стоящего в скобках никак не меняется.

В выполнении рассматриваемых действий нет ничего сложного. Главное запомнить основные требования и придерживаться их в процессе любых вычислений! Если сразу запомнить все правила не получается, заходи на сайт 100уроков.ru и мы всегда с удовольствием напомним нужное правило или алгоритм.

Минутка истории

История математики утверждает, что человечество длительное время не принимало ряд отрицательных числовых значений. Данный вид чисел, казался непонятным и ненужным. Привычных нам знаков «плюс» и «минус» просто не существовало. Если возникала необходимость в записи отрицательно числа, то его записывали следующим образом «долг в 30 монет». И лишь математики Древней Индии и Китая, выполняли записи отрицательных чисел без употребления слова «долг», а просто использовали черные чернила, вместо синих.

Только в 3 веке греческий ученый Диофант, стал обозначать знак «минус» вот таким символом   .

Привычные нам знаки «+» и «-» появились в Германии в конце 15 века. Чешский ученый Ян Видман, отразил данные знаки в своей книге-пособии, помогающей подсчитывать прибыль и убытки чешским купцам. Стоит заметить, что данная книга была написана от руки и имела огромную популярность среди богатых людей того времени.

Математика 5-6 классы. 33. Положительные и отрицательные числа. Модуль числа

Подробности

Категория: Математика 5-6 классы

 Отрицательные целые числа

Термометр, изображенный на рис. 3.1, показывает температуру 7° тепла. Если температура понизится на 4°, то термометр будет показывать 3° тепла. Уменьшению температуры соответствует действие с натуральными числами: 7—4 = 3.

Если температура понизится на 7°, то термометр покажет 0°: 7—7 = 0.Если же температура понизится на 9°, то термометр покажет —2° (2° мороза). Но результат вычитания 7—9 не выражается целым неотрицательным числом, хотя он имеет реальный смысл.Проиллюстрируем вычитание на ряде целых неотрицательных чисел.1) От числа 7 отсчитаем влево 4 числа и получим 3:    

2) От числа 7 отсчитаем влево 7 чисел и получим 0:

Отсчитать же в ряду неотрицательных чисел от числа 7 влево 9 чисел нельзя. Чтобы действие 7—9 стало выполнимым, расширим ряд неотрицательных чисел. Для этого запишем влево от нуля по порядку числа 1,, 2, 3, добавляя к каждому из них знак минус (—), который будет показывать, что число стоит слева от нуля. Эти числа читаются так: «минус один», «минус два»,- «минус три» и т. д.:

Справа от числа 0 расположены натуральные числа, которые еще называют целыми положительными числами.Слева от числа 0 расположены целые отрицательные числа.Число 0 не является ни положительным, ни отрицательным числом. Оно разделяет положительные и отрицательные числа.Полученный нами ряд чисел называется рядом целых чисел. Таким образом, натуральные, целые отрицательные числа и нуль образуют ряд целых чисел. Вправо и влево этот ряд можно продолжать неограниченно.

Правила знаков. Модуль числа

Считают, что если перед целым числом поставить знак плюс (+), то это не изменяет самого числа. Например; 5 = +5, —5 = +(—5).Ряд целых чисел можно записать так:

Целые числа, которые отличаются только знаком, называются противоположными.

Например, 1 и —1, —5 и 5, 10 и-—10 являются противоположными числами.Если перед целым числом поставить знак минус (—), то получается число, ему противоположное: —(+1) =—1, — (—2) =+2.Единственным числом, которое не изменяется, если перед ним поставить знак «—», является число 0; 0 = —0 = +0. Нуль считается противоположным самому себе.Число, противоположное числу а, обозначается —а. Заметим, что —а может быть положительным, отрицательным числом и нулем. Например, если а = + 2, то —а=—2, так как—(+2) =—2; если а=—3, то—а = +3, так как — (—3) = +3; если а — 0, то—а= 0, так как —0 = 0.Введем новое понятие—модуль числа.Модулем положительного числа называется само это число.

Например, модулем числа +3 является +3. Пишут: |+3| = +3.Модулем числа 0 является число 0. Пишут:

Модулем отрицательного числа называется противоположное ему число. Например, модулем числа —4 является число +4. Пишут:

Таким образом, модуль целого числа—положительное число или нуль.Модуль положительного или отрицательного числа показывает, на каком месте от нуля (справа или слева) стоит это число в ряду целых чисел. Противоположные числа имеют одинаковый модуль:

Преобразовать отрицательное число в положительное excel

В программе эксель существует несколько способов преобразовать отрицательное число в положительное. Выбор способа зачастую зависит от поставленной задачи. Давайте рассмотрим подробно многочисленные способы решения данной задачи.

Первый способ. В этом случае рассматриваем пример, когда все изначальные числа отрицательные и их нужно сделать положительными. Перед нами таблица, в которой есть один столбец, состоящий из пяти отрицательных чисел.

Решаем подобную проблему простым умножением каждого числа на минус один, тогда сначала пишем в ячейке «В2» пишем формулу =A2*-1, после копируем её на оставшиеся ячейки.

Второй способ. Сначала скопируем все отрицательные значения в диапазон ячеек «С2» по «С6». В ячейке «А7» поставим цифру -1.

Выделим ячейку «А7» и нажмем на клавиатуре комбинацию клавиш «CTRL+C». После выделяем диапазон ячеек с «С2» по «С6», нажимаем правую клавишу мыши, в появившемся окне выбираем «Специальная вставка».

На экране отобразится меню «Специальная вставка», где в разделе «Операция» ставите точку у строчки «умножение», после закрываем меню через кнопку «ОК» или клавишу «Enter».

В итоге все числа стали положительными, а в ячейках у нас отсутствуют формулы.

Третий способ. Первые два способа подходят для массива данных состоящих из одних отрицательных чисел, когда же присутствует положительные и отрицательные числа, данные способы не подходят. Теперь перед нами таблица со смешанными числами.

Воспользуемся функцией ЕСЛИ, чтобы сначала проверить отрицательное число в ячейке или нет, и в зависимости от этого будет разное решение, тогда в ячейке «В2» напишем функцию: =ЕСЛИ(A2 20.12.2018 Теги: Как сделать, Excel

Обычная формула для вычисления процентного отклонения прекрасно работает до той поры пока не приходиться работать с отрицательными числами. Проверьте стоит нам изменить значение в процентном отношении на отрицательное число в результате мы получаем ОШИБКУ! То есть формула процентного отклонения с отрицательным числом в числителе: = -10 /20-1 или так: =(20- -10 )/10 в любом случаи формулой будет возвращено ошибочное значение -300% . Возникает вопрос откуда появилось минус триста процентов ? Для ответа на этот вопрос и как делать правильно покажем на конкретном примере ниже.

Иррациональные и действительные числа

Долгое время дробей было достаточно человечеству для любых расчетов. Древние греки полагали, что любое отношение величин, которое может встретиться в реальном мире, будет выражаться какой-нибудь дробью. Однако это не так. Один из учеников Пифагора, Гиппас, пытался найти соотношение между стороной квадрата и его диагональю. В результате он осознал, что такой дроби просто не существует.

Это соотношение равно квадратному корню из 2 (что доказывается в курсе геометрии), которое обозначается как . Это такое число, которое при умножении на само себя дает 2. Докажем, что оно не может быть выражено несократимой дробью.

При этом она равна дроби 2/1. Следовательно, b*b = 1 , а a*a = 2. Однако не существует такого натурального числа a, которое при умножении на себя дает 2. Получается противоречие, значит,  нельзя представить в виде дроби. Математики говорят, что  является иррациональным числом. Аналогичным образом можно доказать иррациональность квадратного корня из любого натурального числа, не являющимся квадратом другого натурального числа.

Исторически именно  был первым иррациональным числом, открытым человечеством. Его значение примерно равно 1,414213562. Способы его вычисления будут освещены позже. Заметим лишь, что у этого числа нельзя найти периода в его десятичной записи.

Вообще любое иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби. Это значит, что в числах после запятой не будет никакого периода. Чуть раньше мы уже приводили два примера иррациональных чисел:

• 0,12345678910111213141516…;
• 0,10100100010001000001….

Ещё одним иррациональным числом является π, которое равно отношению длины окружности к ее диаметру и примерно равно 3,1415926…

Для обозначения множества иррациональных чисел используется буква I.

Рациональные и иррациональные числа вместе образуют множество действительных чисел, обозначаемое буквой R. Иногда их также называют вещественными числами.

Слово «вещественное» указывает на физический смысл этого понятия. Любой результат измерения какой-либо величины (длины, площади, объема, массы и т. д.) является вещественным числом.

Важно, что на числовой прямой, или координатной оси, каждой точке в соответствие можно поставить действительное число, и наоборот, каждому действительному числу соответствует единственная точка на числовой прямой. В качестве примера показаны числа π и  на числовой прямой:

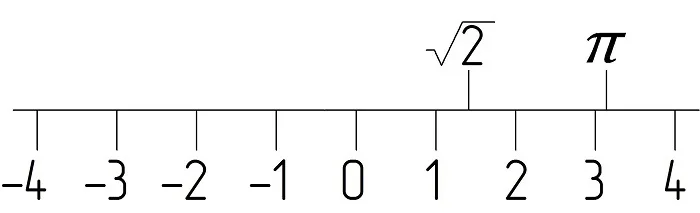
Таким образом, можно составить следующую классификацию чисел, используемых в математике:

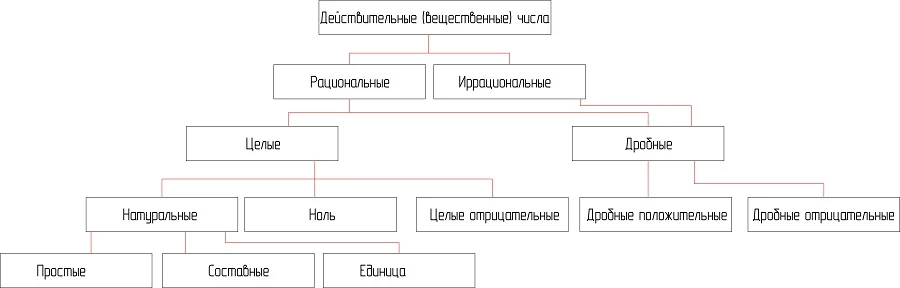
Все числа, которые встретятся в ходе изучения школьной программы математики и других наук, будут действительными. Однако стоит отметить, что в высшей математике, изучаемой в университете, будут изучаться и более сложные объекты, называемые комплексными числами.

Преобразование отрицательных чисел в положительные одним щелчком мыши (VBA)

И, наконец, вы также можете использовать VBA для преобразования отрицательных значений в положительные.

Я бы порекомендовал использовать этот метод, если вам приходится делать это часто. Возможно, вы регулярно получаете набор данных из базы данных или от коллег, и вам нужно делать это каждый раз.

В таком случае вы можете создать и сохранить код макроса VBA в личной книге макросов и разместить VBA на панели быстрого доступа. Таким образом, в следующий раз, когда вы получите набор данных, в котором вам нужно это сделать, вы просто выберите данные и щелкните значок в QAT…

Не волнуйтесь, я покажу вам точные шаги, чтобы запустить его.

Ниже приведен код VBA, который преобразует отрицательные значения в положительные значения в выбранном диапазоне:

Вы можете добавить этот код в обычный модуль в книге (если вы хотите использовать его только в этой книге). И если вы хотите использовать этот код макроса в любой книге в вашей системе, вы можете сохранить его в личной книге макросов.

Теперь позвольте мне показать вам, как добавить этот код на панель быстрого доступа (шаги одинаковы, независимо от того, сохраняете ли вы этот код в отдельной книге или в PMW)

Теперь у вас будет значок макроса в QAT.

Чтобы использовать этот макрос одним щелчком мыши, просто сделайте выбор и щелкните значок макроса.

Примечание. Если вы сохраняете код макроса VBA в книге, вам необходимо сохранить книгу в формате с поддержкой макросов (XLSM).

Когда вы используете Microsoft Excel для работы с числами, вы можете сделать так, чтобы в Excel всегда было положительное число, чтобы найти абсолютное значение числа. Абсолютное значение всегда положительно. В других случаях вы можете предпочесть отображать финансовые данные, используя все положительные числа, причем отрицательные суммы выделены красным или выделены чем-то, кроме знака минус. Используйте формулу ABS в Excel, чтобы получить абсолютное значение и удалить знак, или используйте пользовательское форматирование, чтобы отрицательные числа выглядели положительными.

кредит: fizkes / iStock / GettyImages

Преобразование отрицательных чисел в положительные одним щелчком мыши (VBA)

И, наконец, вы также можете использовать VBA для преобразования отрицательных значений в положительные.

Я бы рекомендовал использовать этот метод, если вам приходится делать это часто. Возможно, вы регулярно получаете набор данных из базы данных или от коллеги, и вам приходится делать это каждый раз.

В таком случае вы можете создать и сохранить код макроса VBA в личной книге макросов и поместить VBA на панель быстрого доступа. Таким образом, в следующий раз, когда вы получите набор данных, где вам нужно это сделать, вы просто выберите данные и щелкните значок в QAT…

… и готово!

Не волнуйтесь, я покажу вам точные шаги, чтобы настроить и запустить его.

Ниже приведен код VBA, который преобразует отрицательные значения в положительные значения в выбранном диапазоне:

Приведенный выше код использует цикл For Next для просмотра каждой выбранной ячейки. Он использует оператор IF, чтобы проверить, является ли значение ячейки отрицательным или нет. Если значение отрицательное, знак меняется на противоположный, а если нет, то игнорируется.

Вы можете добавить этот код в обычный модуль в рабочей книге (если вы хотите использовать его только в этой рабочей книге). И если вы хотите использовать этот код макроса в любой книге вашей системы, вы можете сохранить его в личной книге макросов.

Теперь позвольте мне показать вам, как добавить этот код на панель быстрого доступа (шаги одинаковы, независимо от того, сохраняете ли вы этот код в отдельной книге или в PMW)

Теперь у вас будет значок макроса в QAT.

Чтобы использовать этот макрос одним щелчком мыши, просто сделайте выбор и щелкните значок макроса.

Примечание. Если вы сохраняете код макроса VBA в книге, вам необходимо сохранить книгу в формате с поддержкой макросов (XLSM)

Чтобы преобразовать отрицательные числа в положительные и оставить положительные числа (т. е. получить абсолютные значения), используйте встроенную функцию ABS. В примере показана формула в C6:

Функция ABS полностью автоматическая. Все, что вам нужно сделать, это указать число, и ABS вернет абсолютное значение.

Преобразуйте отрицательные числа на месте

Если вам нужно преобразовать отрицательные числа только один раз, вы можете преобразовать на месте с помощью специальной вставки:

1. Добавить -1 к ячейке и скопировать в буфер обмена
2. Выберите отрицательные числа, которые хотите преобразовать.
3. Используйте «Специальная вставка» > «Значения + умножение».

В видео на этой странице показан этот метод и многие другие специальные сочетания клавиш для вставки.

СЧЁТЕСЛИ подсчитывает количество ячеек в диапазоне, соответствующих заданным критериям. В этом случае критерии предоставляются как «

В этом примере цель состоит в том, чтобы преобразовать отрицательные числа в столбце B в ноль и оставить положительные числа без изменений. По сути, мы хотим заставить отрицательные числа равняться нулю. С функцией MAX Функция MAX предлагает элегантное решение: = MAX (.

Функция ABS в Excel возвращает абсолютное значение числа. ABS преобразует отрицательные числа в положительные, а на положительные числа это не влияет.

Синтаксис числового форматирования

Обычно числовое форматирование применяется следующим образом: выделяется ячейка или диапазон ячеек (1), к которому нужно числовой формат применить, и затем из выпадающего списка (2) выбирается готовый шаблон (3).

Как правило, пользователи не интересуются, как именно этот шаблон работает, а просто применяют готовые форматы в своей работе.

Также все готовые шаблоны доступны и в окне Формат ячеек .

Здесь в самом конце списка находится пункт « все форматы », который позволяет посмотреть на код, используемый в готовых шаблонах, а также создавать свои форматы.

Для создания формата нужно понимать синтаксис написания кода, то есть нужно изучить правила, по которым он формируется и узнать, какие вспомогательные символы в коде используются.

Именно об этом я и расскажу в этой заметке.

Итак, код числового формата в общем случае состоит из четырех разделов:

ПОЛОЖИТЕЛЬНЫЕ; ОТРИЦАТЕЛЬНЫЕ; НОЛЬ; ТЕКСТ

Сначала указывается правило форматирования положительных значений, затем отрицательных, далее нулевых и в конце текста. Все четыре раздела отделяются друг от друга точкой с запятой.

При этом необязательно в коде должны присутствовать все четыре раздела.

Если задан только один раздел, то он будет применяться ко всем числовым значениям вне зависимости от их величины и знака. Если указано два раздела, то первый будет использоваться для форматирования положительных числовых значений и нулей, а второй для отрицательных чисел. И только указание всех четырех разделов в коде позволит форматировать текстовые значения.

Код каждого раздела числового формата задается с помощью специальных символов. Давайте их рассмотрим на примерах и пока будем использовать самый простой шаблон — зададим только один раздел для всех числовых значений.

Как сделать изучение отрицательных чисел легче для шестиклассников

Организация: МАОУ «Средняя общеобразовательная школа №36»

Населенный пункт: г.Кемерово

«Нельзя из меньшего отнять большее»- скажет вам любой школьник до пятого класса. И правда, ведь курс математики до 6 класса основан только на положительных числах. Поэтому шестиклассники, которые начинают знакомиться с отрицательными числами очень часто испытывают сложности.

«Это не логично! Так не работает» — говорили мои ученики на первом занятии по отрицательным числам. Потому что именно в этот момент для шестиклассников открывается новая сторона математики. Ведь «-15» больше не погода в приложении на смартфоне, теперь это слагаемое или даже множитель.

Поэтому хочется сделать так, чтоб знакомство с отрицательными числами проходило легче и интереснее. У меня за время работы в школе накопилось несколько идей как заинтересовать шестиклассников этой темой и как подружить их с отрицательными числами.

1. Введение отрицательных чисел через понятие “долг”. Начиная уже со школьного возраста, дети придают большое значение финансам. Поэтому понятие «долг» шестиклассники представляют в реальной жизни. «Петя взял у Славы в долг 50 рублей», значит у Пети остаётся «-50», т.е. Петя должен 50 рублей. Так же понятие «долг» помогает формировать школьниками одно из направлений функциональной грамотности- финансовую грамотность.
2. Исходя из первого пункта можно выделить следующий: использование примеров из реальной жизни, где отрицательные числа могут быть полезны. Например, температура может быть отрицательной, если она ниже нуля или можно показать, что высота может быть отрицательной в случае, если вы находитесь ниже уровня моря. Также можно предлагать примеры с «ямой»: линия — земли- это ноль, если «-9», то вырыли на 9 метров вниз, если «+8», то яму засыпали на 8 метров. Следовательно, пример «-6+10», можно представить, как «яму глубиной 6 метров засыпали на 10 метров. 6 метров ушло под землю, 4 осталось над землей».
3. Создание графиков и диаграмм, которые показывают, как отрицательные числа связаны с положительными. Это поможет ученикам визуализировать отрицательные числа и понять их место на числовой прямой.
4. Решение задач с отрицательными числами. Ученики могут решать задачи, в которых нужно вычитать, а не складывать. Например, можно предложить им задачу о том, сколько денег они потратили, если их баланс на карточке уменьшился на определенную сумму.
5. Решение задач с отрицательными числами. Ученики могут решать задачи, в которых нужно вычитать, а не складывать. Например, можно предложить им задачу о том, сколько денег они потратили, если их баланс на карточке уменьшился на определенную сумму.

Но немало важный момент- это то, как мы будем знакомить школьников с отрицательными числами

В данном вопросе тоже очень важно подобрать правильный подход. Будет неправильно и грубо если отрицательными числа просто «вывалить» на детей

Необходимо сделать так, чтоб им было интересно узнать о низ больше. Введение через историю: Расскажите ученикам об отрицательных числах в контексте их исторического развития. Это может помочь им лучше понять, почему они существуют и как они используются. Визуализация: Используйте графики, диаграммы и другие визуальные материалы, чтобы помочь ученикам лучше понять отрицательные числа. Игры и головоломки: Создайте игры или головоломки, которые помогут ученикам лучше понять отрицательные числа и их использование.

Эти подходы помогут замотивировать шестиклассников. Замотивированные дети на уроке — это хорошо. Они будут более активно участвовать в уроке, задавать вопросы, пытаться понять материал. Это может привести к более глубокому пониманию материала и лучшему обучению в целом.

В заключение хочется сказать, что математика — это не только наука о числах и формулах, но и искусство познания мира. Благодаря математике мы можем понимать и описывать сложные явления, предсказывать события и создавать новые технологии

Поэтому так важно, чтобы учителя математики не только знали свой предмет, но и умели передать свою страсть к нему своим ученикам. Используя различные методы и подходы в обучении, учителя могут сделать процесс изучения математики более увлекательным и доступным для каждого ученика

Опубликовано: 26.02.2024

Героические поступки простых людей

В 1997 г. высшая награда нашей страны была впервые вручена девушке — Плотниковой Марине (посмертно). Свой подвиг она совершила в июле 1991 г. в Томалинском районе Пензенской области. Марина вместе с двумя своими младшими сестрами купалась в реке Хопёр. К ним присоединилась подруга – Наташа Воробьева, которая вскоре попала в водоворот и начала тонуть. Марина спасла ее. Однако в это время в водоворот попали ее младшие сестры. Мужественная девушка смогла спасти и их, однако сама выбилась из сил и, к несчастью, погибла.

И пусть не все подвиги простых людей в наши дни оцениваются наградой Героя России. Но, тем не менее, этих граждан нашей страны можно считать таковыми. И несмотря на то что подвиги простых людей в наши дни порой малозаметны, но они навсегда остаются в благодарных сердцах людей.

Уважения и восхищения достоин героический поступок семидесятидевятилетней Елены Голубевой. Она первая поспешила на помощь людям, пострадавшим во время крушения «Невского экспресса». Пожилая женщина отнесла им одежду и свои одеяла.

Настоящими героями города Искитима (Новосибирская область) стали два студента местного монтажного техникума. Ими, 17-летним Никитой Миллером и 20-летним Владом Волковым, был скручен налетчик, который попытался ограбить продуктовый ларек.

Не растерялся в сложной ситуации священник из Челябинской области Алексей Перегудов. Ему пришлось спасать жизнь жениху прямо на свадьбе. Парень потерял сознание во время венчания. Иерей Перегудов, осмотрев лежащего, предположил у него остановку сердца. Тут же священник принялся оказывать первую помощь. После выполнения непрямого массажа сердца, который Перегудов раньше видел только по телевизору, жених пришел в себя.

В Мордовии героический поступок совершил Марат Зинатуллин. Этот ветеран войны в Чечне спас пожилого мужчину, вытащив его из горящей квартиры. Увидев пламя, Марат забрался на крышу находящегося рядом с домом сарая, а оттуда смог попасть на балкон. Зинатуллин разбил стекло и попал в квартиру, где на полу лежал отравившийся дымом 70-летний пенсионер. Марат смог открыть входную дверь и вынести пострадавшего в подъезд.

30.11.2013 г. на Черноисточинском пруду провалился под лед рыбак. Мужчине пришел на помощь работник аварийной службы жилищно-коммунального хозяйства Раис Салахутдинов. Он также рыбачил на этом пруду и первый услышал крик о помощи.

Сложение чисел с разными знаками

Рассмотрим ситуацию.

Мишин папа навещал бабушку в деревне, обещал привезти гостинец сыну – яблоки. Во дворе Миша рассказал мальчишкам про папино обещание, и решил угостить яблоком, каждого из трех друзей, то есть, у него уже стало -3 яблока. Папа привез сыну 10 яблок и мальчик с радостью поделился фруктами с друзьями. Сколько яблок осталось у мальчика?

Чтобы найти количество яблок у мальчика, нам нужно узнать, чему равна сумма яблок –тех которые были у мальчика(-3), и тех, которые дал папа(10). То есть, чтобы ответить на главный вопрос задачи, достаточно сложить -3 и 10. Но слагаемые имеют разные знаки «+» и «-». Как же выполнить сложение положительного и отрицательного чисел? Запомнив алгоритм сложения положительных и отрицательных чисел сделать это, будет очень просто.

Используем рассмотренный алгоритм при выполнении действий.

Суммируем-3 и 10. Для этого:

• определяем модули: -3=|3|, 10=|10|;
• сравниваем модули, определяя больший: |3|<|10|;
• от большего отнимаем меньший: 10 – 3=7;
• так как по условию 10 – число положительное, то и результат будет числом положительным.

Записывается в таком виде:

-3+10=10 – 3=7.

Выходит, у мальчика стало 7 яблок.

Рассмотрим еще один пример сложения чисел с разными знаками.

Вычислите сумму -28 и 11.

Известные слагаемые имеют разные знаки, то есть -28 является значением отрицательным, а 11–положительным. Чтобы суммировать слагаемые, необходимо воспользоваться ранее рассмотренным алгоритмом. Вначале, определяем модули и сравниваем их.

-28=|28|;

11=|11|;

28>11.

Помним, что большее значение модуля имеет отрицательное слагаемое (-28), поэтому перед результатом нужно будет поставить знак «минус». Теперь, находим разность большего и меньшего значения модуля (28-17) и записываем математическое выражение:

-28+11=-(28-11)=-17.

Учитывая рассмотренные примеры, можно сказать, что:

любое числовое значение от прибавления к нему положительного числа, всегда становится больше, а от прибавления отрицательного числа только меньше.

Докажем справедливость данного правила, вычислив выражение и сравнив уменьшаемое с полученной суммой:-150+50.

Чтобы найти значение выражения нужно определить модули (150 и 50), оставив знак«-» модуля большего слагаемого, от большего значения отнимаем меньшее:

-150+50=-(150-50)=-100.

Сравним найденное значение выражения (-100) с уменьшаемым (-150), используя правило сравнения чисел с отрицательным знаком:

При сравнении цифровых значений со знаком «минус», меньшим будет то, чей модуль больше.

-150=|150|;

-100=|100|.

150>100;

-150<-100.

Действительно, при сложении с отрицательным числом уменьшаемое стало только меньше.

Практические примеры

В повседневной жизни минус на минус может использоваться для различных расчетов и операций. Ниже представлены несколько практических примеров, где принцип минус на минус, равный плюс, применим.

1. Вычитание долга. Предположим, вы одалживали у друга деньги на неопределенный срок и через некоторое время решили вернуть долг. Если последний раз запись о долге велась с отрицательным знаком (минусом), вычетание долга по принципу минус на минус превратит его в положительное число (плюс).

2. Исправление ошибки в вычислениях. При выполнении сложных математических операций, таких как последовательные вычитания или умножения, ошибки могут возникнуть из-за неправильного знака. Например, при вычитании -5 — (-2) вместо ожидаемого -3 можно получить -5 + 2, что даст -3. Такая ситуация может возникнуть и при других сложных вычислениях, и здесь применение минус на минус поможет получить правильный результат.

3. Перевод температуры. В некоторых случаях, при переводе температуры из одной шкалы в другую, может возникнуть ситуация, когда температура изначально выражена отрицательным числом. В таких случаях принцип минус на минус может быть использован для получения правильного значения в другой шкале. Например, -10 градусов Цельсия соответствуют +14 градусам Фаренгейта.

Это лишь несколько примеров, которые показывают практическую применимость принципа минус на минус, равного плюс. В реальной жизни такие ситуации могут возникать достаточно часто, и понимание этого принципа поможет избежать ошибок в расчетах и получить верные результаты.