Все треугольники и их названия. свойства треугольника

Определение косинуса двойного угла через синус двойного угла:

Как найти косинус, синус и тангенс угла в непрямоугольном треугольнике?

Для нахождения косинуса, синуса и тангенса угла в непрямоугольном треугольнике можно использовать формулы, которые основаны на соотношениях между сторонами треугольника. Косинус угла равен отношению прилежащего катета к гипотенузе, синус угла равен отношению противолежащего катета к гипотенузе, а тангенс угла равен отношению противолежащего катета к прилежащему катету. Для нахождения этих функций, необходимо знать длины сторон треугольника или иметь другие данные о треугольнике.

где α — значение угла в непрямоугольном треугольнике.

Косинус двойного угла также может быть найден с использованием рядов или таблицы значений функций углов треугольника. Для нахождения косинуса двойного угла можно использовать следующую формулу:

Сумма углов треугольника

В невырожденном треугольнике существуют разные типы углов:

1. Острые углы — углы, меньшие 90°;
2. Прямой угол — угол, равный 90°;
3. Тупой угол — угол, больший 90°, но меньший 180°.

Теорема о сумме углов треугольника утверждает, что в невырожденном треугольнике сумма углов всегда равна 180°. Это свойство можно доказать несколькими способами, например через параллельные линии или с использованием проекций.

Сумма углов в треугольнике можно найти с помощью формулы α + β + γ = 180°, где α, β и γ — углы треугольника.

Пользуясь этой формулой, можно определить тип треугольника по его углам:

• Треугольник с тремя острыми углами называется остроугольным, если все его углы меньше 90°;
• Треугольник с одним прямым углом называется прямоугольным;
• Треугольник с одним тупым углом называется тупоугольным.

Кроме того, сумма углов треугольника связана с его высотой. В прямоугольных треугольниках, высота проходит через прямой угол, а в остроугольных и тупоугольных треугольниках, высоты опускаются из вершин на стороны треугольника.

Также, сумма углов треугольника связана с площадью треугольника. С помощью высоты можно вычислить площадь треугольника по формуле S = 1/2 * a * h, где a — основание треугольника, h — высота. Или можно воспользоваться формулой S = 1/2 * b * c * sin(α), где b и c — боковые стороны треугольника, α — угол между ними.

В общем случае, треугольник можно классифицировать по различным свойствам, таким как равные стороны, равные углы, соотношение между сторонами внутри треугольника (например, теорема Пифагора), подобие с другими треугольниками и т.д.

Связь невырожденного треугольника с другими геометрическими фигурами

Невырожденный треугольник обладает рядом свойств и связей с другими геометрическими фигурами:

1. Прямоугольный треугольник: Если один из углов невырожденного треугольника равен 90 градусов, то такой треугольник называется прямоугольным. В прямоугольном треугольнике один из углов является прямым углом, а вторые два угла являются остроугольными или тупыми. Такой треугольник имеет множество интересных свойств, включая теорему Пифагора.

2. Равносторонний треугольник: Если все стороны невырожденного треугольника равны между собой, то такой треугольник называется равносторонним. У равностороннего треугольника все три угла равны 60 градусам, и он обладает множеством уникальных свойств, таких как равенство высот, биссектрис и медиан.

3. Равнобедренный треугольник: Если две стороны невырожденного треугольника равны между собой, то такой треугольник называется равнобедренным. У равнобедренного треугольника два угла равны между собой, а оставшийся угол может быть разным. Такой треугольник обладает рядом интересных свойств, таких как равенство биссектрис, связанных с основанием треугольника, и равенство углов при вершине.

4. Треугольник равноугольный: Если все углы невырожденного треугольника равны между собой, то такой треугольник называется равноугольным или равнобедренным. В равноугольном треугольнике все углы равны между собой и равны 60 градусам. Такой треугольник обладает множеством интересных свойств, включая равенство высот, биссектрис и медиан.

5. Треугольник подобный: Невырожденный треугольник может быть подобным другому треугольнику, если их соответствующие углы равны между собой. Подобные треугольники имеют пропорциональные стороны и подобные углы, что позволяет строить аналогии в их свойствах и отношениях.

Эти связи невырожденного треугольника с другими геометрическими фигурами являются основой для решения геометрических задач и доказательства теорем. Они позволяют строить связи и обобщения между различными фигурами и углублять понимание геометрии.

Нормированное векторное пространство

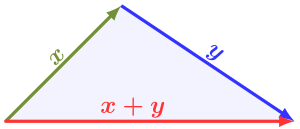Неравенство треугольника для норм векторов.

В нормированное векторное пространство V, одно из определяющих свойств норма это неравенство треугольника:

‖Икс+у‖≤‖Икс‖+‖у‖∀Икс,у∈V{ displaystyle displaystyle | x + y | leq | x | + | y | quad forall , x, y in V}

то есть норма не больше суммы норм двух векторов. Это также называется субаддитивность. Чтобы любая предлагаемая функция вела себя как норма, она должна удовлетворять этому требованию.

Если нормированное пространство евклидов, или, в более общем смысле, строго выпуклый, тогда ‖Икс+у‖=‖Икс‖+‖у‖{ Displaystyle | х + у | = | х | + | у |} если и только если треугольник, образованный Икс, у, и Икс + у, является вырожденным, то естьИкс и у находятся на одном луче, т.е. Икс = 0 или у = 0, илиИкс = α y для некоторых α > 0. Это свойство характеризует строго выпуклые нормированные пространства, такие как ℓ_п пространства с 1 < п < ∞. Однако есть нормированные пространства, в которых это неверно. Например, рассмотрим самолет с ℓ₁ норма ( Манхэттенское расстояние ) и обозначить Икс = (1, 0) и у = (0, 1). Тогда треугольник, образованныйИкс, у, и Икс + у, невырожден, но

‖Икс+у‖=‖(1,1)‖=|1|+|1|=2=‖Икс‖+‖у‖.{ Displaystyle | х + у | = | (1,1) | = | 1 | + | 1 | = 2 = | х | + | у |.}

Примеры норм

Абсолютное значение как норма для реальная линия. Чтобы быть нормой, неравенство треугольника требует, чтобы абсолютная величина удовлетворять для любых реальных чисел Икс и у:

|Икс+у|≤|Икс|+|у|,{ Displaystyle | х + у | Leq | х | + | у |,}

что он делает.

Доказательство:

−|Икс|≤Икс≤|Икс|{ displaystyle — left vert x right vert leq x leq left vert x right vert}

−|у|≤у≤|у|{ displaystyle — left vert y right vert leq y leq left vert y right vert}

После добавления

−(|Икс|+|у|)≤Икс+у≤|Икс|+|у|{ Displaystyle — ( влево верт х вправо верт + влево верт у вправо верт) Leq х + у Leq влево верт х вправо верт + влево верт у вправо vert}

Используйте тот факт, что |б|≤а⇔−а≤б≤а{ displaystyle left vert b right vert leq a Leftrightarrow -a leq b leq a}(с участием б заменяется Икс+у и а от |Икс|+|у|{ displaystyle left vert x right vert + left vert y right vert}), у нас есть

|Икс+у|≤|Икс|+|у|{ Displaystyle | х + у | Leq | х | + | у |}

Неравенство треугольника полезно в математический анализ для определения наилучшей верхней оценки размера суммы двух чисел в терминах размеров отдельных чисел.

Существует также более низкая оценка, которую можно найти с помощью обратное неравенство треугольника в котором говорится, что для любых действительных чисел Икс и у:

|Икс−у|≥||Икс|−|у||.{ displaystyle | x-y | geq { bigg |} | x | — | y | { bigg |}.}

Внутренний продукт как норма в внутреннее пространство продукта. Если норма возникает из внутреннего произведения (как в случае евклидовых пространств), то неравенство треугольника следует из Неравенство Коши – Шварца следующим образом: данные векторы Икс{ displaystyle x} и у{ displaystyle y}, и обозначив внутренний продукт как ⟨Икс,у⟩{ Displaystyle langle х, у rangle}:

‖Икс+у‖2{ Displaystyle | х + у | ^ {2}}	=⟨Икс+у,Икс+у⟩{ displaystyle = langle x + y, x + y rangle}
	=‖Икс‖2+⟨Икс,у⟩+⟨у,Икс⟩+‖у‖2{ displaystyle = | x | ^ {2} + langle x, y rangle + langle y, x rangle + | y | ^ {2}}
	≤‖Икс‖2+2|⟨Икс,у⟩|+‖у‖2{ Displaystyle Leq | х | ^ {2} +2 | langle x, y rangle | + | y | ^ {2}}
	≤‖Икс‖2+2‖Икс‖‖у‖+‖у‖2{ Displaystyle Leq | х | ^ {2} +2 | х | | у | + | у | ^ {2}} (по неравенству Коши – Шварца)
	=(‖Икс‖+‖у‖)2{ Displaystyle = влево ( | х | + | у | вправо) ^ {2}}.

Неравенство Коши – Шварца превращается в равенство тогда и только тогда, когда Икс и улинейно зависимы. Неравенство⟨Икс,у⟩+⟨у,Икс⟩≤2|⟨Икс,у⟩|{ displaystyle langle x, y rangle + langle y, x rangle leq 2 | langle x, y rangle |}превращается в равенство для линейно зависимых Икс{ displaystyle x} и у{ displaystyle y}тогда и только тогда, когда один из векторов Икс или у это неотрицательный скаляр другого.

Извлечение квадратного корня из окончательного результата дает неравенство треугольника.

п-норма: обычно используемой нормой является п-норма:

‖Икс‖п=(∑я=1п|Икся|п)1п ,{ Displaystyle | х | _ {p} = left ( sum _ {i = 1} ^ {n} | x_ {i} | ^ {p} right) ^ {1 / p} ,}

где Икс_я компоненты вектора Икс. Для п = 2 то п-норма становится Евклидова норма:

‖Икс‖2=(∑я=1п|Икся|2)12=(∑я=1пИкся2)12 ,{ Displaystyle | х | _ {2} = влево ( сумма _ {я = 1} ^ {п} | х_ {я} | ^ {2} вправо) ^ {1/2} = влево ( sum _ {i = 1} ^ {n} x_ {i} ^ {2} right) ^ {1/2} ,}

который Теорема Пифагора в п-размеры, очень частный случай, соответствующий внутренней норме продукта. Кроме случая п = 2, то п-норма не внутренняя норма продукта, потому что она не удовлетворяет закон параллелограмма. Неравенство треугольника для общих значений п называется Неравенство Минковского. Он принимает вид:

‖Икс+у‖п≤‖Икс‖п+‖у‖п .{ displaystyle | x + y | _ {p} leq | x | _ {p} + | y | _ {p} .}

Таблицы и графики функции cos

Функция cos отображает значения косинуса угла в непрямоугольном треугольнике. Чтобы упростить нахождение значений этой функции, были разработаны таблицы и графики.

Таблица функции cos представляет собой упорядоченный набор значений угла и соответствующих ему значений косинуса. Зная значение угла, можно быстро определить соответствующий ему косинус, что упрощает расчеты в задачах trigonometry. Также таблица cos позволяет найти обратную функцию — арккосинус (или арккосинус), что полезно при решении уравнений, связанных с косинусом угла.

График функции cos представляет собой графическое представление значений косинуса угла от угла. Он позволяет визуально оценить изменение функции cos и выделить особые точки, такие как максимум и минимум. График также позволяет сравнить функцию cos с другими тригонометрическими функциями, такими как синус и тангенс.

Таблицы и графики функции cos широко применяются в математике, физике, инженерии и других областях, где требуется работа с углами и тригонометрическими функциями. Они являются незаменимыми инструментами для решения задач со связанными углами и сторонами непрямоугольных треугольников, а также для проведения анализа колебаний, смены сезонов и других явлений, связанных с периодическими процессами.

Значимость невырожденных треугольников

Невырожденные треугольники являются основным строительным блоком геометрии и имеют большое значение в различных научных и практических областях. Они широко используются в архитектуре, инженерии, физике, графике и других науках.

Вот несколько основных причин, почему невырожденные треугольники являются важными:

1. Определение формы и размера: Невырожденные треугольники обладают четко определенной формой и размером. Используя их в качестве основного элемента для построения, архитекторы и инженеры могут создавать прочные и устойчивые сооружения. Например, пирамиды в Египте и готические соборы в Европе строятся на основе треугольников.
2. Вычисления и измерения: Треугольники являются одной из наиболее изученных геометрических фигур. Их свойства и формулы используются для вычислений и измерений в различных областях. Например, в геодезии треугольники используются для определения расстояний и углов на земной поверхности.
3. Графическое моделирование и анимация: Треугольники используются как основные элементы в компьютерной графике и анимации. В трехмерной графике объекты обычно представляются в виде множества треугольников, которые затем обрабатываются компьютером для создания реалистичных изображений и анимации.
4. Триангуляция: Треугольники играют важную роль в геометрии и алгоритмах триангуляции. Триангуляция представляет собой разбиение геометрической фигуры на невырожденные треугольники. Этот процесс используется в различных областях, таких как картография, сеточное моделирование и компьютерная графика.
5. Перспектива и пропорции: Треугольники используются для создания эффекта перспективы и определения пропорций в изображении. В искусстве и дизайне треугольники могут использоваться для создания глубины и тримерного вида, а также для соблюдения пропорций и гармонии в композиции.

Таким образом, невырожденные треугольники играют важную роль в различных областях, от строительства и наук о материалах до компьютерной графики и искусства. Понимание и использование треугольников позволяют нам лучше понять и описать мир вокруг нас.

Свойства различных типов треугольников

Как упоминалось ранее, существует три типа треугольников в зависимости от их углов: остроугольные, прямоугольные и тупоугольные. Каждый из этих треугольников обладает уникальными свойствами, которые делают их важными в различных ситуациях.

Тип треугольника	Свойства
Остроугольный треугольник	Все углы меньше 90 градусов. Сумма углов 180 градусов. Все стороны не равны.
Прямоугольный треугольник	Один угол равен ровно 90 градусам. Сумма углов 180 градусов. Сторона, противоположная прямому углу, называется гипотенузой, и это самая длинная сторона. Две другие стороны называются катетами.
Тупоугольный треугольник	Один угол больше 90 градусов. Сумма углов 180 градусов. Сторона, противоположная тупому углу, является самой длинной стороной.

Понимание свойств различных типов треугольников необходимо для решения задач в математике, физике и технике. Если вы строите мост, рассчитываете траекторию спутника или просто решаете геометрическую задачу, треугольники играют решающую роль во многих областях науки и техники.

Основные величины и их формулы

Все геометрические фигуры имеют свои характеристики и собственную величину. Самыми распространёнными являются такие величины как площадь и периметр. Они используются в повседневной жизни, в строительстве и в других областях. Например, во время ремонта или нового строительства, количество необходимых материалов и объём работ не определить, не вычислив заранее площадь и периметр.

Периметр

Периметром называется замкнутая граница плоской геометрической фигуры, которая отделяет её внутреннюю область от внешней. Периметр есть у любой замкнутой геометрической фигуры:

На рисунке периметры выделены красной линией. Периметр окружности часто называют длиной.

Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.

Обозначается заглавной латинской P.

Площадь

Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой, то есть та часть плоскости, которая находится внутри периметра. Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь. 

На рисунке площади фигур окрашены различными цветами.

Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм2, см2, м2, км2 и т. д. S (square) — знак площади.

Вычисление периметра и площади

Периметр — это длина замкнутого контура геометрической фигуры. Можно, конечно, измерить линейкой длины всех сторон и сложить их. Но лучше воспользоваться специальными формулами для вычисления периметра, это значительно упростит задачу.

• Квадрат: периметр = 4 * сторона.
• Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.
• Неправильный многоугольник: периметр = сумме всех сторон многоугольника.
• Круг: длина окружности = 2 * π * радиус = π * диаметр (где π – это число пи (константа, примерно равная 3,14), радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности, диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности).

Для вычисления площади фигуры также потребуется соответствующая формула. К разным фигурам применяются разные формулы. Для вычисления площади стандартных геометрических фигур можно воспользоваться следующими формулами:

• Параллелограмм: площадь = основание * высота
• Квадрат: площадь = сторона 1 * сторона 2
• Треугольник: площадь = ½ * основание * высота
• Круг: площадь = π * радиус² (где радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя).

Итак, мы перечислили основные и самые распространённые геометрические фигуры и их свойства. Образовательная платформа iSmart поможет вашему ребёнок изучить основные геометрические фигуры, их виды, названия и свойства с помощью увлекательных заданий. Преимущества занятий на умных тренажёрах iSmart:

• интерактивные задания больше похожи на игру;
• их можно отрабатывать многократно и они не будут повторяться;
• платформа сформирует индивидуальную траекторию обучения на основе диагностики знаний;
• достаточно всего 20 минут занятий в день, чтобы в короткий срок увидеть прогресс в обучении.

Кроме того, занятия помогут вам освободить своё время, ведь ребёнок сможет заниматься самостоятельно, а родитель — получать отчёты и наблюдать за динамикой обучения. Метод обучения iSmart основан на последних научных практиках: микрообучение и поведенческий анализ.

Образовательная платформа iSmart предлагает подготовку к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.

Что такое треугольник

Рассмотрим понятие треугольника. Пусть на плоскости дана трехзвенная замкнутая ломаная. Тогда эта ломаная разделяет множество оставшихся точек плоскости на ограниченную и неограниченную фигуры. При этом ограниченная фигура называется частью плоскости, ограниченной данной ломаной. Например, на рисунке 59, а изображена часть плоскости, ограниченная трехзвенной замкнутой ломаной ABC.

Определение. Треугольником называется геометрическая фигура, состоящая из трехзвенной замкнутой ломаной и части плоскости, ограниченной этой ломаной.

Вершины ломаной называются вершинами треугольника, а звенья ломаной — сторонами треугольника.

Точки треугольника, не принадлежащие его сторонам, называются внутренними.

Треугольник, вершинами которого являются точки А, В и С, обозначается следующим образом:

АВС
BСА
CАВ

На рисунке 59, а изображен треугольник ABC. Точки А, В и С — вершины этого треугольника, а отрезки AB, ВС и АС — его стороны. На рисунке 59, B показан треугольник AFD, содержащийся в грани куба.

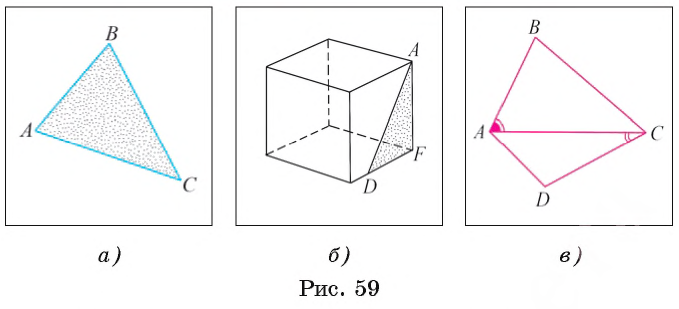
Углы АBС, АСВ и САВ (см. рис. 59, а) называются внутренними углами треугольника ABC или просто углами треугольника. Иногда они обозначаются одной буквой:

A,
B,
CСтороны и углы треугольника называются его элементами.

На рисунке 59, в изображены треугольники ABC и ACD, у которых общая сторона АС. Угол ВАС — внутренний угол треугольника ВАС,

ACD

Периметром треугольника называется сумма длин всех его сторон. Периметр треугольника ABC обозначается P_ABC.

Конструкции, имеющие треугольную форму, применяются при строительстве архитектурных сооружений, мостов и жилых зданий. Например, при постройке крыш некоторых домов используются стропила, имеющие форму треугольников (рис. 60, а).

Для треугольников, как и любых геометрических фигур, определяется понятие их равенства.

Два треугольника называются равными, если их можно совместить наложением, т. е. можно совместить их вершины, стороны и углы.

Рассмотрим пример. Если лист бумаги, имеющий форму прямоугольника, разрезать на две части, как показано на рисунке 60, б, то мы получим модели равных треугольников. Непосредственно можно убедиться, что полученные части можно наложить одна на другую так, что они совместятся.

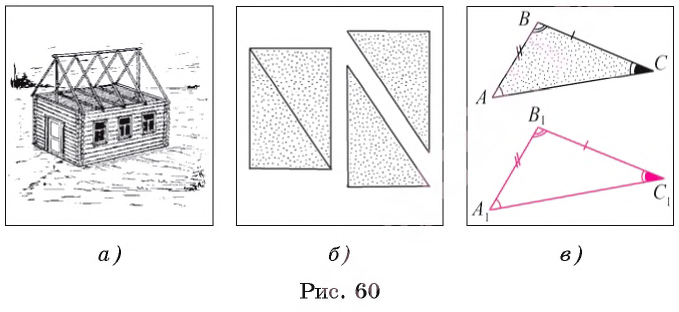
Два равных треугольника ABC и A₁B₁C₁(рис. 60, в) можно совместить так, что попарно совместятся их вершины, стороны и углы. Другими словами, если два треугольника равны, то стороны и углы одного треугольника соответственно равны сторонам и углам другого треугольника. Подчеркнем, что:

• в равных треугольниках против соответственно равных сторон лежат равные углы;
• в равных треугольниках против соответственно равных углов лежат равные стороны.

Например, в равных треугольниках ABC и A₁B₁C₁, изображенных на рисунке 60, в, против равных сторон ВС и В₁С₁лежат равные углы А и А₁. Против равных углов С и С₁ лежат равные стороны AB и A₁B₁.

Если треугольники ABC и A₁B₁C₁ равны, то это обозначается следующим образом:

ABC
A₁B₁C₁

Заметим, что для установления равенства треугольников необязательно их совмещать один с другим, а достаточно сравнить некоторые их элементы (стороны и углы).

Для доказательства равенства треугольников пользуются соответствующими теоремами (признаками), которые позволяют на основании равенства некоторых элементов треугольников делать вывод о равенстве самих треугольников.

Вопросы

1. Что такое треугольник?
   
2. Виды треугольников?
   
3. В чем особенность египетского треугольника?
   
4. Где применяется египетский треугольник?
   > Математика 8 класс
   

Строительство с применением египетского треугольника древний способ, активно используемый до сих пор современными строителями. Название получил благодаря древнеегипетским сооружениям, хотя известно, что история его начинается задолго до этого периода.

Но, скорее всего, свойства уникальной фигуры не были оценены в те времена, пока не появился Пифагор, сумевший проанализировать и оценить изящные формы фигуры.

Египетский треугольник известен еще с древних времен. Он был и остается популярен в строительстве и архитектуре много веков.

Считается, что создал геометрическую конструкцию великий греческий математик Пифагор Самосский. Благодаря ему сегодня мы можем использовать все свойства геометрической постройки в области строения.

Зарождение идеи

Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.

Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.

Из истории

Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.

Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса
, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51 о 50’.

Строение

Задача намного облегчается, если использовать транспортир или треугольник. Но, раньше применялись только шнуры и веревке, разделенные на отрезки. Благодаря отметкам на веревке можно было с точностью воссоздать прямоугольную фигуру. Строителям заменяла транспортир и угольник веревка, для чего отмечали узлами на ней 12 частей и складывали треугольник с отрезками 3,4,5. Прямой угол получался без затруднений. Эти знания помогли создать множество сооружений, в том числе пирамиды.

Свойства египетской треугольной фигуры подчиняются истине – квадрат гипотенузы равен квадратам двух катетов. Эта теорема Пифагора знакома каждому со школьной поры. Например, умножаем 5х5 и получаем гипотенузу равную числу 25. Квадраты обоих катетов равны 16 и 9, что в сумме дает цифру 25.

Благодаря таким свойствам, треугольник нашел применение в строительстве. Можно взять любую деталь, с целью провести линию прямого направления с условием, что ее длина должна быть кратной пяти. После этого заметить один край и прочертить от него линию кратную четырем, а от другого кратную трем. При этом каждый отрезок должен быть длиной минимум четыре и три. Пересекаясь, они образовывают один прямой угол в 90 градусов. Другие углы равны 53,13 и 36,87 градусам.

Свойства

Определение невырожденного треугольника в геометрии основано на том, что углы треугольника суммируются в 180 градусов, каждая сторона больше нуля, и сумма двух сторон всегда больше третьей стороны. Любая грань треугольника является отрезком, соединяющим две его вершины.

Примерами невырожденных треугольников могут служить треугольник со сторонами 3, 4 и 5, а также треугольник с углами 30, 60 и 90 градусов.

Равенство суммы углов треугольника 180 градусам.

Стандартное определение треугольника в геометрии — это фигура, образованная тремя сторонами и тремя вершинами. Каждая сторона соединяет две вершины, а каждый угол образуется двумя сторонами, исходящими из одной вершины. Углы треугольника также могут быть классифицированы как острые (меньше 90 градусов), прямые (равные 90 градусам) или тупые (больше 90 градусов).

Признак невырожденного треугольника — это условие, при котором сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Иначе говоря, треугольник должен быть «закрытой» фигурой, а не прямой линией или точкой.

Важным свойством невырожденного треугольника является равенство суммы углов треугольника 180 градусам. Это значит, что сумма всех внутренних углов треугольника равна 180 градусам. Например, если у нас есть треугольник с углами 60 градусов, 70 градусов и 50 градусов, то их сумма будет равна 180 градусам.

Сумма длин двух сторон треугольника всегда больше длины третьей стороны.

В геометрии треугольник представляет собой плоскую фигуру, образованную тремя отрезками, называемыми сторонами треугольника. Каждая сторона треугольника является гранью этой фигуры, а точки их пересечения – вершинами. Сумма длин двух сторон определенного треугольника всегда больше длины третьей стороны и служит важным признаком для определения невырожденного треугольника.

Позвольте рассмотреть пример, чтобы увидеть это свойство в действии. Предположим, что у нас есть треугольник с сторонами длиной 5, 7 и 10 единиц. Чтобы проверить, выполняется ли свойство суммы длин двух сторон, необходимо сложить длины двух самых коротких сторон:

Стороны треугольника	Сумма длин двух сторон
5, 7, 10	5 + 7 = 12

Как видим, сумма длин двух сторон треугольника равна 12. Затем сравниваем эту сумму с длиной третьей стороны:

Стороны треугольника	Сумма длин двух сторон	Длина третьей стороны
5, 7, 10	12	10

Как можно заметить, сумма длин двух сторон (12) больше длины третьей стороны (10), что подтверждает наше утверждение о том, что сумма длин двух сторон треугольника всегда больше длины третьей стороны.

Сумма длин двух сторон треугольника является важным свойством, она влияет на множество других характеристик треугольника, таких как его площадь, углы и отношения между сторонами.

Высоты треугольника пересекаются в одной точке — ортоцентре.

Одним из важных свойств треугольника является то, что все высоты треугольника пересекаются в одной точке, которая называется ортоцентром. Именно ортоцентр является точкой пересечения трех высот треугольника.

Ортоцентр имеет много геометрических свойств и является ключевой точкой в задачах треугольника. Он лежит внутри или на границе треугольника, в зависимости от его типа и положения высот. Более того, ортоцентр может быть использован для определения других важных элементов треугольника, таких как окружность Эйлера и описанная окружность.

Одно из основных свойств ортоцентра заключается в том, что отрезки, соединяющие ортоцентр с вершинами треугольника, перпендикулярны соответствующим сторонам. Это означает, что углы между сторонами треугольника и этими отрезками равны 90 градусам.

Еще одним важным признаком ортоцентра является его связь с площадью треугольника. Для любого треугольника, площадь треугольника ABC равна произведению половины основания BC на высоту, проведенную из вершины A:

SABC = 0.5 * BC * HA, где SABC — площадь треугольника ABC, BC — основание треугольника, HA — высота, проведенная из вершины A.

Таким образом, ортоцентр треугольника имеет большое значение и определение его свойств позволяет углубить понимание треугольника в геометрии. Благодаря своей особенной природе, ортоцентр является важным элементом в решении задач и определении основных характеристик треугольника.

Значение понятия «Невырожденный треугольник»

Невырожденный треугольник — это треугольник, который имеет конечные стороны и углы, а также положительную площадь. Такой треугольник является основным объектом изучения геометрии и математики.

Значит, треугольник, который не является невырожденным, будет иметь одну или несколько из следующих характеристик:

• Одна или несколько сторон имеют нулевую длину. В этом случае треугольник превращается в отрезок или точку.
• Одна или несколько сторон имеют отрицательную длину. Это может происходить, когда точки, задающие стороны треугольника, расположены в неправильном порядке.
• Сумма длин двух сторон меньше третьей стороны. Такой треугольник называется вырожденным, и он не может существовать в двумерном пространстве.
• Один или несколько углов равны 0 или 180 градусов. Такие углы называются вырожденными углами и не отличаются от прямой линии или плоскости.

Имея эти определения в виду, мы можем утверждать, что для треугольника с конечными сторонами и положительной площадью справедливо понятие «невырожденный треугольник». Это базовое понятие является основой для изучения свойств и характеристик треугольников в геометрии.

Основные характеристики невырожденного треугольника

Что значит невырожденный треугольник? Невырожденный треугольник — это треугольник, у которого все три стороны положительной длины и никакие три точки, задающие его вершины, не лежат на одной прямой.

Вот основные характеристики, которые отличают невырожденный треугольник:

• Три стороны: невырожденный треугольник имеет три стороны, каждая из которых имеет положительную длину и является отрезком прямой между двумя вершинами.
• Три вершины: треугольник имеет три вершины, которые являются точками пространства или плоскости. Вершины образуют углы друг с другом.
• Три угла: треугольник состоит из трех углов, которые образуются между сторонами. Сумма всех углов в невырожденном треугольнике равна 180 градусам.
• Площадь: невырожденный треугольник имеет площадь, которая можно вычислить с использованием формулы Герона или других методов.
• Периметр: периметр невырожденного треугольника — это сумма всех его сторон. Он также может быть вычислен с помощью известных значений длин сторон.

Невырожденный треугольник является одной из основных фигур в геометрии. Он имеет множество свойств и характеристик, которые могут быть использованы для изучения его свойств и применения в различных математических и физических задачах.

Различия невырожденного треугольника от вырожденного

Треугольник — это геометрическая фигура, состоящая из трех отрезков, которые соединяются между собой в трех точках. Однако не все треугольники являются невырожденными, и это имеет свои особенности и значения.

Невырожденный треугольник (также известный как обычный треугольник) — это треугольник, у которого все три стороны имеют разную длину и все три угла не равны нулю и не равны 180 градусов. Невырожденный треугольник значит, что он имеет достаточно размеров и формы, чтобы считаться полноценным и функциональным треугольником.

Основное отличие невырожденного треугольника от вырожденного заключается в его свойствах и определениях. Невырожденный треугольник имеет три разные стороны и три угла, которые в сумме равны 180 градусов. Каждая сторона невырожденного треугольника соединяет две точки, и каждый угол образуется между двумя сторонами. Такой треугольник может быть измерен и описан с помощью геометрических формул и правил.

В то же время, вырожденный треугольник имеет особые свойства и определения. Он представляет собой треугольник, у которого все три стороны соединены в одной точке, а все три угла равны нулю или 180 градусов. Это значит, что его стороны и углы не образуют полноценной фигуры у треугольника и не могут быть измерены с помощью геометрических формул.

Таким образом, различия между невырожденным и вырожденным треугольниками заключаются в их свойствах и определениях. Невырожденный треугольник является полноценной геометрической фигурой с тремя разными сторонами и углами в сумме, равной 180 градусов, в то время как вырожденный треугольник не обладает такими свойствами и не может быть измерен с помощью геометрических формул.

Примеры использования формулы вычисления косинуса в непрямоугольном треугольнике

Формула вычисления косинуса в непрямоугольном треугольнике позволяет определить значение косинуса угла треугольника по значениям его сторон.

Рассмотрим несколько примеров использования этой формулы:

1. Пример 1:

   Рассмотрим треугольник ABC, в котором известны значения сторон a = 5, b = 3 и угол γ = 60°.

   Для вычисления косинуса этого угла можно использовать формулу:

   cos(γ) = (a^2 + b^2 — c^2) / (2ab)

   Подставляем известные значения в формулу:

   cos(60°) = (5^2 + 3^2 — c^2) / (2 * 5 * 3)

   cos(60°) = (25 + 9 — c^2) / 30

   Решаем уравнение:

   30 * cos(60°) = 25 + 9 — c^2

   Раскрываем скобки и упрощаем:

   15 = 34 — c^2

   c^2 = 34 — 15

   c^2 = 19

   c ≈ √19

   Таким образом, значение стороны c приближенно равно √19.

2. Пример 2:

   Рассмотрим треугольник XYZ, в котором известны значения сторон x = 4, y = 7 и угол α = 45°.

   Для вычисления косинуса этого угла можно использовать формулу:

   cos(α) = (x^2 + y^2 — z^2) / (2xy)

   Подставляем известные значения в формулу:

   cos(45°) = (4^2 + 7^2 — z^2) / (2 * 4 * 7)

   cos(45°) = (16 + 49 — z^2) / 56

   Решаем уравнение:

   56 * cos(45°) = 16 + 49 — z^2

   Раскрываем скобки и упрощаем:

   28√2 = 65 — z^2

   z^2 = 65 — 28√2

   z ≈ √(65 — 28√2)

   Таким образом, значение стороны z приближенно равно √(65 — 28√2).

3. Пример 3:

   Рассмотрим треугольник PQR, в котором известны значения сторон p = 9, q = 6 и угол β = 30°.

   Для вычисления косинуса этого угла можно использовать формулу:

   cos(β) = (p^2 + q^2 — r^2) / (2pq)

   Подставляем известные значения в формулу:

   cos(30°) = (9^2 + 6^2 — r^2) / (2 * 9 * 6)

   cos(30°) = (81 + 36 — r^2) / 108

   Решаем уравнение:

   108 * cos(30°) = 117 — r^2

   Раскрываем скобки и упрощаем:

   54√3 = 117 — r^2

   r^2 = 117 — 54√3

   r ≈ √(117 — 54√3)

   Таким образом, значение стороны r приближенно равно √(117 — 54√3).

Тригонометрические функции в непрямоугольном треугольнике

В непрямоугольном треугольнике можно определить значения синуса и косинуса углов с помощью рядов. Так, значения синуса угла А будут равны сумме ряда:

А значения косинуса угла А равны сумме ряда:

Тангенс угла А определяется как отношение синуса к косинусу того же угла:

Точность вычислений тригонометрических функций через ряды зависит от количества взятых членов ряда. Чем больше членов ряда учтено, тем более точные результаты можно получить. Однако при приближении значения угла А к 0, 180, 360 и другим значениям кратным углов, формулы тригонометрических функций через ряды могут выдать неудовлетворительные результаты, так как значения функций здесь определяются через деление на ноль.