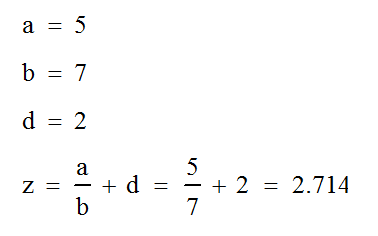Функция арктангенса в excel

Шаг 3: Ввести формулу для арктангенса

Для вычисления арктангенса в Mathcad необходимо использовать специальную функцию «arctan», которая принимает на вход значение аргумента и возвращает соответствующий результат.

Чтобы ввести формулу для арктангенса в Mathcad, выполните следующие действия:

Откройте новый документ Mathcad или выберите существующий.
Создайте новую ячейку, в которой будет располагаться формула для арктангенса.
Напишите следующую формулу: arctan(x), где x — значение аргумента, для которого нужно вычислить арктангенс.
Заполните ячейку соответствующим значением аргумента (x).
Выполните расчет, нажав на кнопку «Вычислить» или нажав клавишу Enter.
Получите результат вычисления арктангенса в ячейке.

Теперь вы знаете, как ввести формулу для арктангенса в Mathcad и вычислить его значение.

Как записать арктангенс в MathCad

Для записи арктангенса в MathCad следует использовать функцию arctg, arctgx или atan. Все они являются синонимами и используются для вычисления арктангенса числа. Вводится функция арктангенса следующим образом: arctg(x), arctgx(x) или atan(x), где x — число, для которого необходимо найти арктангенс.

Например:

arctg(0) равен 0;
arctg(1) равен π/4 радиан;
arctg(-1) равен -π/4 радиан;
arctg(√3) равен π/3 радиан.

Также можно вычислить арктангенс в градусах, для этого нужно за функцией arctg(x) добавить модификатор deg:

С какого устройства вы смотрите видео на YouTube?

С компьютераС телефона

arctg(1)deg равен 45°;
arctg(√3)deg равен 60°.

Кроме того, арктангенс можно записать в виде логарифма:

arctg(x) = ln((1+x)/(1-x))/(2i), где i — мнимая единица. Эта формула позволяет вычислить арктангенс как комплексную функцию.

Использование арктангенса в MathCad позволяет решать широкий спектр задач, связанных с тригонометрическими функциями и вычислениями.

Шаг 3: Включаем режим «Градусы» на калькуляторе

Для того чтобы включить режим «Градусы» на калькуляторе Windows 10, следуйте этим простым инструкциям:

Откройте калькулятор, нажав на кнопку «Пуск» и вводя «калькулятор» в поле поиска. Затем выберите приложение «Калькулятор».
Нажмите на кнопку «Вид» в верхнем левом углу калькулятора.
В раскрывающемся меню выберите «Инженерный калькулятор», чтобы открыть расширенные функции калькулятора.
Нажмите на кнопку «Режим» в верхней части калькулятора. В появившемся меню выберите «Градусы».

Теперь калькулятор будет работать в режиме «Градусы», что позволит вам вычислять арктангенс и другие тригонометрические функции с использованием градусов вместо радиан.

📸 Видео

Mathcad Prime. Урок 4 — тригонометрические функции MathcadСкачать

Вычисление аркфункцийСкачать

Вычисление простых выражений в MathCAD 14 (4/34) Часть 1Скачать

4. MathCad. Функции, функции пользователя, производные и первообразныеСкачать

Как работать с программой mathCadСкачать

Научитесь считать в Mathcad Express за 1 часСкачать

Математика это не ИсламСкачать

Программа MathCAD. Урок 10. Работа с матрицами в MathCADСкачать

Дискретные переменные в MathCAD 14 (9/34)Скачать

Аппроксимация данных произвольной функцией в Mathcad. Функция genfitСкачать

Плоский график функции в MathCAD 14 (10/34)Скачать

Другие математические функции в Excel

Excel – это мощный инструмент, который позволяет выполнять различные математические операции. Кроме функции Арктангенс, Excel предлагает множество других математических функций, которые могут быть полезны в работе с таблицами.

Функция МОД – вычисляет остаток от деления одного числа на другое. Она может использоваться, например, для определения четности или нечетности числа.

Функция СРЗНАЧ – вычисляет среднее арифметическое значение ячеек в заданном диапазоне. Она часто используется для анализа статистических данных.

Функция МАКС и МИН – вычисляют наибольшее и наименьшее значение в заданном диапазоне соответственно. Они могут быть использованы для поиска экстремальных значений в таблице.

Функция СУММ – вычисляет сумму ячеек в заданном диапазоне. Она часто используется для расчета общих значений.

Функция ОКРУГЛ – округляет заданное число до указанного количества знаков после запятой.

Это далеко не все математические функции, которые предлагается использовать в Excel. Каждая функция может быть полезной в зависимости от требуемых целей таблицы.

Как записать арктангенс в маткаде

Система MathCAD содержит большой набор встроенных элементарных функций. Функции задаются своими именами и значениями аргумента, заключёнными в круглых скобках. Функции, как и переменные, и числа, могут входить в состав математических выражений. В ответ на обращение к ним, функции возвращают вычисленные значения. Ниже представлены некоторые из этих функций.

1.2.1 Тригонометрические функции

sin (z) — синус . cos (z) — косинус tan (z) — тангенс . sec (z) — секанс csc (z) — косеканс . cot (z) — котангенс

1.2.2 Гиперболические функции

sinh (z) — гиперболический синус cosh(z) — гиперболический косинус tanh(z) — гиперболический тангенс sech(z) — гиперболический секанс csch(z) — гиперболический косеканс coth(z) — гиперболический котангенс

1.2.3 Обратные тригонометрические функции

asin (z) — арксинус acos(z) — арккосинус atan(z) — арктангенс

1.2.3 Обратные тригонометрические функции

asin (z) — арксинус acos(z) — арккосинус atan(z) — арктангенс

1.2.4 Обратные гиперболические функции

asinh (z) — обратный гиперболический синус acosh(z) — обратный гиперболический косинус atanh(z) — обратный гиперболический тангенс

1.2.5 Показательные и логарифмические функции

exp (z) — экспоненциальная функция ln (z) — натуральный логарифм log (z) — десятичный логарифм

1.2.6 Функции с условиями сравнения

ceil (x) — наименьшее целое, большее или равное х floor(x) — наибольшее целое, меньшее или равное х mod(x,y) — остаток отделения х/у со знаком х angle(x,y) — положительный угол с осью х для точки с координатами (х,у)

MathCAD. MatLab

Если этого не сделать, то • atan(X) – возвращает арктангенс для каждого элемента X. Для действи тельных значений X atan(X) находится в области [–?/2, . Пример: >> Y=atan(1) Y= 0.7854 • atan2 (Y, X) – возвращает массив P той же размерности что X и Y, содер жащий поэлементно арктангенсы отношения вещественных частей Y и X. Мнимые части игнорируются. Элементы P находятся в интервале [–?, . Специфический квадрант определен функциями sign(Y) и sign(X). Это

174 Программные средства математических вычислений отличает полученный результат от результата atan(Y/X), который огра ничен интервалом [–?/2, . Пример: >> atan2(1,2) ans = 0.4636 Встроенные элементарные функции 175 • cos(X) – возвращает косинус для каждого элемента X. Пример: >> X=; >> cos(X) ans = 0.5403 >> Y = cot(2) Y= -0.4577 -0.4161 -0.9900 • cot(X) – возвращает котангенс для каждого элемента X. Пример: • csc(O) – возвращает косеканс для каждого элемента X. Пример: >> X=; >> Y = csc(X) Y= 1.0998 -1.0006 -1.0428 1.1985 1.1884 7.0862 • sec(X) – возвращает массив той же размерности, что и X, состоящий из секансов элементов X. Пример: >> X=[pi/10 pi/3 pi/5]; >> sec(X) ans = 1.0515 2.0000 1.2361 Рис. 3.2. Графики четырех тригонометрических функций • sin(X) – возвращает синус для каждого элемента X. Пример: >> X=[pi/2 pi/4 pi/6 pi]; >> sin(X) ans = 1.0000 0.7071 0.5000 тронных устройств. Следующая программа строит графики для таких комбина ций, создающих из синусоиды три наиболее распространенных сигнала – прямо угольные, пилообразные и треугольные импульсы1 : % I?ia?aiia iino?iaiey a?aoeeia neaiaeia x=-10:0.01:10; subplot(2,2,1),plot(x,0.8*sin(x)). xlabel(\’0.8*sin(x)\’) subplot(2,2,2),plot(x,0.8*sign(sin(x))). xlabel(\’0.8*sgn(sin(x))\’) subplot(2,2,3),plot(x,atan(tan(x/2))). xlabel(\’atan(tan(x/2))\’) subplot(2,2,4),plot(x,asin(sin(x))). xlabel(\’asin(sin(x))\’) 0.0000 • tan(X) – возвращает тангенс для каждого элемента X.

Зачем использовать арктангенс в MathCad?

Арктангенс позволяет определить угол, чей тангенс равен определенному значению. Это полезно в различных областях науки и техники, например:

Тригонометрия и геометрия: Арктангенс используется для определения углов в треугольниках и решения различных геометрических задач.
Электроника и телекоммуникации: В этих областях арктангенс применяется для расчета фазовых сдвигов и углов сигналов в синусоидальных системах.
Робототехника и автоматизация: Арктангенс используется для определения углов поворота и направления движения роботов и автоматических систем.
Научные исследования: Арктангенс применяется в различных областях научных исследований, например, для анализа данных, построения графиков и моделирования физических процессов.

Использование арктангенса в MathCad позволяет эффективно решать математические и инженерные задачи, связанные с определением углов и преобразованием координат.

Как правильно записать Arcctg()

arctg пишется как atan А как записать arcctg? Гугл не помогает.

Нашел, будет acot

Изображения94731 / 64177 / 26122
Регистрация: 12.04.2006
Сообщений: 116,782
Ответы с готовыми решениями:

Как правильно записать F(x)Как правильно записать F(x) чтоб реализовать метод простой итерации

Как правильно записать?Записываю интеграл как есть ,а он выдаёт странное решение,помогите, как правильно записать?

Как правильно записать выражение?Здравствуйте. Есть исходные данные: Есть выражение: Для каждого значения VH нужно получить.

Как записать правильно формулу?не могу записать фор-лу,постоянно что-то горит красным..

Практические примеры использования арктангенса

Арктангенс, или обратная тангенс функция, очень полезна в научных расчётах и инженерных приложениях. Вот несколько примеров использования арктангенса:

Вычисление угла:

Предположим, у нас есть прямоугольный треугольник с катетами a = 3 и b = 4. Чтобы найти угол α между гипотенузой и катетом a, мы можем использовать формулу:

α = atan(a/b) = atan(3/4)

Результатом будет угол α, выраженный в радианах.

Навигация в пространстве:

Предположим, у нас есть мобильный робот, который может двигаться вперёд и поворачивать. Он знает длину прямого пути и угол поворота. Чтобы найти расстояние между двумя точками, на которых оказался робот в результате движения, мы можем использовать формулу:

расстояние = sqrt((a^2) + (b^2))

где a — длина прямого пути, а b — длина пути, смещённого в сторону на угол поворота, выраженный в радианах.

Расчёт экспоненциальной функции:

Арктангенс может использоваться вместе с другими функциями, такими как экспоненциальная функция, для расчёта сложных выражений. Например, мы можем использовать формулу:

y = atan(e^x)

чтобы найти значение y для заданного x.

Это лишь некоторые примеры использования арктангенса в научных расчётах. Эта функция может быть полезной, когда вам нужно работать с углами, навигацией или сложными выражениями.

Расчет угла наклона

Для расчета арктангенса в Маткаде можно использовать функцию atn(x), где x – аргумент функции, выражающий отношение противоположной или вертикальной сторон равнобедренного треугольника к его основанию, или, иначе говоря, отношение изменения координаты «y» к изменению координаты «x».

Пример использования функции atn(x) для расчета арктангенса в Маткаде:

x := 2;
y := 4;
угол_наклона := atn(y/x);

В данном примере переменные «x» и «y» представляют собой координаты точки на плоскости, а переменная «угол_наклона» содержит вычисленное значение арктангенса, представляющее угол наклона.

Таким образом, использование функции atn(x) в Маткаде позволяет легко и точно рассчитать угол наклона для различных научных расчетов и приложений.

Навигационные расчеты

Арктангенс (или арктангенсус) — это обратная функция тангенса, позволяющая определить угол, значение тангенса которого известно. В Маткаде арктангенс вычисляется с помощью функции atan().

Для примера, рассмотрим ситуацию, когда известны значения проекции x и проекции y в прямоугольной системе координат. Для нахождения угла между линией, проходящей через начало координат и точку с координатами (x, y), можно воспользоваться формулой:

угол = atan(y/x)

Для решения данной задачи в Маткаде необходимо записать следующую инструкцию:

Данная инструкция позволяет получить значение угла в радианах. Если необходим результат в градусах, его можно получить, умножив значение на коэффициент:

угол (в градусах) = угол (в радианах) * 180 / Пи

Таким образом, для получения угла в градусах в Маткаде необходимо использовать следующую инструкцию:

Примером использования арктангенса в навигации может служить определение угла направления движения судна относительно некоторой исходной точки. Навигационные расчеты с использованием арктангенса могут быть применены для определения направления широты и долготы, определения корректировок магнитного направления и других задач, в которых требуется определить угол между двумя линиями или плоскостями.

Пример использования в физических экспериментах

Допустим, в физическом эксперименте мы измеряем угол падения света на определенную поверхность и хотим найти угол преломления. Для этого мы можем использовать арктангенс.

Пусть у нас есть измеренный угол падения θ₁, а также известны показатели преломления для двух сред: n₁ — показатель преломления среды, из которой идет свет, и n₂ — показатель преломления среды, в которую происходит преломление. Тогда угол преломления θ₂ можно найти по формуле:

θ₂ = atan(n₁/n₂ * tan(θ₁))

Таким образом, арктангенс позволяет нам рассчитать угол преломления в физическом эксперименте на основе измеренных данных

Это является важной и полезной функцией при моделировании и анализе различных физических явлений

Шаг 2: Импорт библиотек в MATLAB

Чтобы построить функцию арктангенса в MATLAB, нам потребуется импортировать несколько библиотек, которые предоставляют необходимые математические функции.

Первой библиотекой, которую мы импортируем, является библиотека Math. Она предоставляет основные математические функции, такие как sin, cos и tan. Мы можем импортировать эту библиотеку, используя следующую команду:

import java.lang.Math;

Далее, нам нужно импортировать еще одну библиотеку — BigDecimal. Эта библиотека используется для работы с десятичными числами с фиксированной точностью. Мы можем импортировать ее следующей командой:

import java.math.BigDecimal;

После импорта этих библиотек мы сможем использовать функции, необходимые для построения функции арктангенса.

Получение функции арктангенса

Предположим, что имеется некая функция:

\(y=\operatorname {tg}\,x\).

Заметим, что эта функция имеет вид кусочно-монотонной. Такая ситуация наблюдается на любом участке области определения. В результате нельзя назвать функцией:

\(y=\operatorname {arctg}\,x\)

Это связано с нарушением условий однозначности. Проанализируем участок, где функция является возрастающей и имеет каждое значение лишь однажды:

\(\left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right).\)

Отрезок \(y=\operatorname {tg}\,x\) отличается тем, что здесь функция является монотонно возрастающей со всеми своими значениями, которые она принимает только однажды.

Можно сделать вывод, что на отрезке \(\left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)\) имеется обратная функция \(y=\operatorname {arctg}\,x \) с графиком, симметричным графическому изображению \(y=\operatorname {tg}\,x\) на участке \(\left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)\) по отношению к прямой \(y=x\).

Понятие арктангенса

Арктангенс для числа х является значением угла у, которое определено в радианах и характеризуется \(\operatorname {tg} y=x,\quad -{\frac {\pi }{2}}\)

Область определения для функции \(y=\operatorname {arctg}x\) распространяется на всю прямую с числами, не прерывается и обладает ограничениями. Такая функция строго возрастает на графике.

\(\operatorname {tg}\,(\operatorname {arctg}\,x)=x, если при x\in {\mathbb R},\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

\(\operatorname {arctg}\,(\operatorname {tg}\,y)=y\), когда если \(-{\frac {\pi }{2}}<y<{\frac {\pi }{2}}\),

\(D(\operatorname {arctg} \,x)=(-\infty ;\infty )\) (область определения),

\(E(\operatorname {arctg}\,x)=\left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)\) (область значений).

Функция arctg обладает следующими свойствами, которые полезно использовать при расчете:

\(\operatorname {arctg}(-x)=-\operatorname {arctg}x\qquad \)(функция не является четной);
\(\operatorname {arctg} x=\arcsin {\frac {x}{\sqrt {1+x^{2}}}}\);
\(\operatorname {arctg}x=\arccos {\frac {1}{{\sqrt {1+x^{2}}}}},\) если \(x > 0\);
\(\operatorname {arctg} x=\operatorname {arcctg} {\frac {1}{x}}\);
\(\operatorname {arctg} x=-i\operatorname {arth} {ix}\), при \(\operatorname {arth}\) в виде обратного гиперболического тангенса, гиперболического ареатангенса.
\(\operatorname {arth} x=i\operatorname {arctg} {ix}\).

Работа с формулами в PTC Mathcad

Как правило, пользователям приходится осуществлять в PTC Mathcad расчет формул, которые оформляются следующим образом:

Пример выполнения данного ряда функций можно увидеть на рисунке ниже:

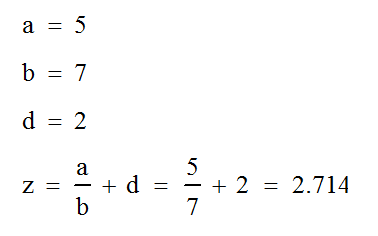
Благодаря этой статье вы узнаете, как функции float и explicit упрощают редактирование формул в процессе работы с программным компонентом PTC Mathcad.

Первым делом нужно определиться с переменными, из которых собственно и состоит конкретная рабочая формула, присвоив им соответствующие численные значения:

После этого можно задать имя итоговой переменной и требуемое выражение:

Обычно панель рабочих символов изначально открывается при запуске системы PTC Mathcad. В противном случае её можно открыть самостоятельно, перейдя на вкладку Вид. Там необходимо будет отыскать специальную Панель инструментов и открыть еще одну вкладку под названием «Символьные». Теперь в строке выражения заданных инструментов достаточно будет выбрать команду explicit. Она автоматически присвоит буквенным параметрам требуемые значения формулы. После выполнения всех этих процедур на рабочем поле отобразится специальный оператор в виде курсора. Рядом высветится уже знакомое слово explicit.

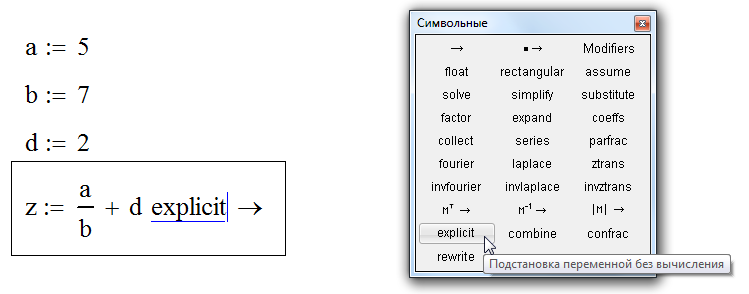
Для грамотного расчета формулы нужно будет вручную ввести команду ALL через запятую от explicit. Она выступит в роли модификатора, который указывает на необходимость подстановки в формулу всех имеющихся переменных. После этого за пределами выражения команды нужно будет нажать левую клавишу мышки, чтобы получить результат расчета:

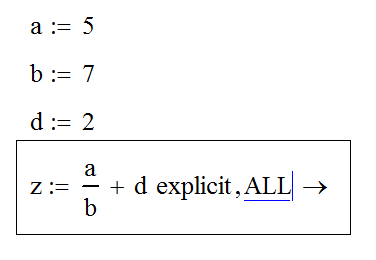
Если вы хотите задать конкретное число знаков после запятой, которое должно отобразиться на экране в результате расчетов, тогда через выражение с помощью курсора можно воспользоваться еще одной полезной функцией – float:

После соответствующей надписи в специально отведенном месте необходимо будет записать требуемое число десятичных разрядов. Таким образом, вы зададите точность расчетов, которая будет сохраняться при любых вычислениях и в случаях подстановки таких результатов в дальнейшие расчеты:

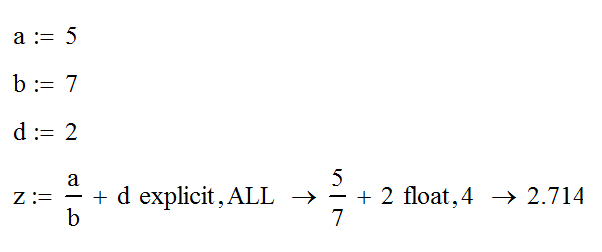
Теперь останется только спрятать ключевые слова и избавиться от стрелок, которые нужно будет в обязательном порядке заменить символами равенства. Аналогичные изменения должны также коснуться имеющихся операторов присваивания. Выделив требуемое выражение с помощью правой клавиши, достаточно будет запустить функцию «Отображать определение как» и в специальном разделе выбрать «Знак равенства», как видно из рисунка ниже:

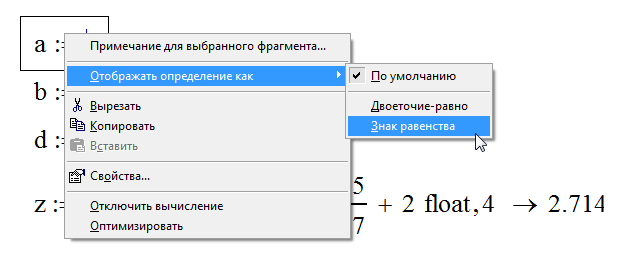
Так непривычные операторы присваивания преобразятся и примут облик знакомого нам всем знака «равно»:

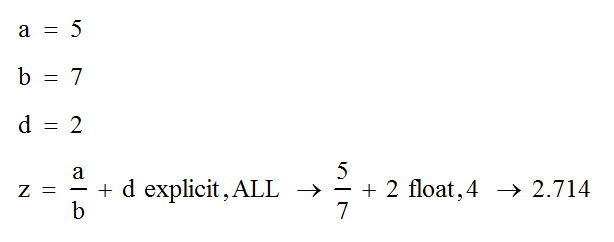
Теперь нужно будет зафиксировать выражение с вычислениями с помощью курсора и тоже задать «Знак равенства» в графе «Отображать вычисления как»:

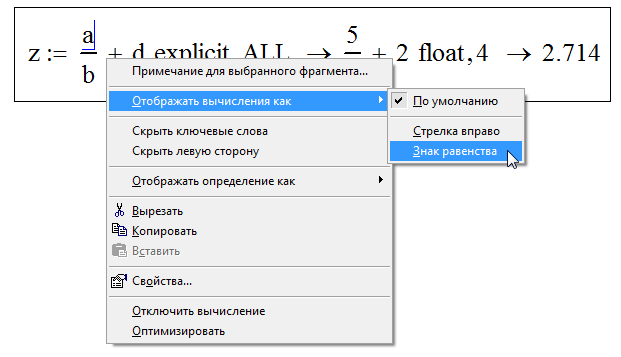
Только на данном этапе расчета стрелки будут автоматически заменены традиционными знаками равенства:

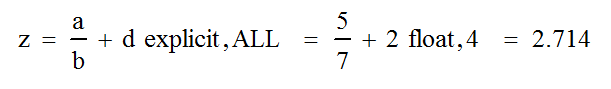
Повторным нажатием правой клавиши в районе выражения вы сможете выполнить функцию «Скрыть ключевые слова»:

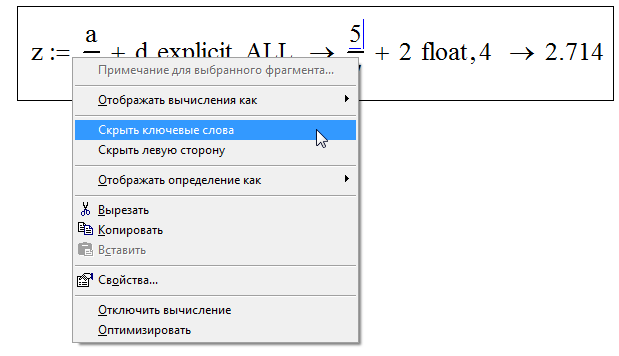
Данная процедура позволит пользователю спрятать лишние команды и функции из виду, чтобы привести формульные выражения к требуемому внешнему виду:

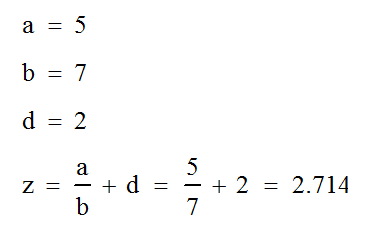
Если вы работаете с PTC Mathcad Prime, порядок подстановки значений в формульную функцию остается без изменений. Единственным недостатком такого программного средства является отсутствие возможности прятать ключевые слова команд и менять внешний вид операторов:

Шаг 1: Определение цели проекта

В данном проекте мы будем работать со встроенными функциями MATLAB, а также реализуем алгоритмы, основанные на ряде Тейлора и других математических подходах. Затем мы сравним и оценим точность полученных результатов, а также скорость работы различных реализаций функции арктангенса.

Для достижения цели проекта мы будем выполнять следующие шаги:

Шаг 1	Определение цели проекта
Шаг 2	Изучение основных свойств функции арктангенса
Шаг 3	Разработка и реализация алгоритма нахождения арктангенса
Шаг 4	Тестирование и сравнение различных реализаций
Шаг 5

Определение цели проекта позволяет нам четко определить направление работы и план действий. Далее мы перейдем к изучению свойств функции арктангенса и выбору подходящего алгоритма для ее реализации.

Почему нужно записывать арктангенс в маткаде?

Арктангенс является одним из элементарных математических функций, которая является обратной функцией тангенса. Записывая арктангенс в маткаде, мы можем проводить различные математические операции с этой функцией и использовать ее в аналитических вычислениях.

Арктангенс, обозначаемый обычно как arctg или atan, является функцией, которая возвращает угол, значение тангенса которого равно заданному числу. Например, если мы хотим найти угол, для которого тангенс будет равен 1, мы можем использовать функцию арктангенса, чтобы получить значение этого угла.

В программе Mathcad, котации для арктангенса могут отличаться в зависимости от версии. В старых версиях программы для обозначения арктангенса используется функция atg, в более современных версиях используются функции atan или arctg.

Запись арктангенса в маткаде позволяет нам выполнять такие операции, как нахождение угла по значению тангенса, нахождение значений функции арктангенса для заданных углов, проведение математических операций с функцией арктангенса и т.д.

Выводы и результаты, полученные при помощи записи арктангенса в маткаде, могут быть использованы в различных областях науки и техники, включая физику, электротехнику, инженерное дело и другие области, где необходимы точные вычисления и аналитические решения.

Шаг 3: Создание переменных и задание начальных значений

На следующем шаге необходимо создать переменные, которые будут использоваться в процессе построения функции арктангенса. В данном примере будут использоваться переменные x, eps, sum и term.

Переменная x будет использоваться для задания значения аргумента функции арктангенса. В этом примере будем считать, что значение аргумента равно 1. Для задания значений переменных можно использовать оператор присваивания, например:

Переменная eps будет использоваться для задания точности вычислений. В данном случае будем считать, что точность равна 0.0001:

Переменные sum и term будут использоваться для вычисления ряда, представляющего функцию арктангенса. Переменная sum будет служить для хранения суммы последовательных членов ряда, а переменная term – для хранения текущего члена ряда:

Теперь, когда переменные созданы и им присвоены начальные значения, можно переходить к следующему шагу – вычислению значения функции арктангенса.

Пример использования функции atan

Функция atan в программе MathCad предназначена для вычисления арктангенса числа

Важно заметить, что в MathCad эту функцию можно записывать как atan, а также в виде arctan

Как записать арктангенс в MathCad с указанием основания?

Для вычисления арктангенса с указанием основания в MathCad вам нужно использовать функцию atan2(). Она принимает два аргумента: y и x, и вычисляет арктангенс отношения y/x.

Вот как выглядит запись функции atan в MathCad:

Где x — число, для которого необходимо найти арктангенс.

Для выполнения вычислений в радианах вместо арктангенса можно использовать функции atan2 или atan2d. Они позволяют определить арктангенс с учетом четверти, в которой находится x и y координаты.

Вот как выглядит запись функции atan2 в MathCad:

Где y и x — координаты точки.

Функции atan2 и atan2d возвращают значение арктангенса в радианах. Если вам нужно получить арктангенс в градусах, можно воспользоваться функцией atan2d.

Например, чтобы найти арктангенс числа 1, вы можете использовать следующую формулу:

Решая эту формулу в MathCad, вы получите результат:

0,7854 радиан (или около 45 градусов).

Также, можно воспользоваться функцией atan2, чтобы найти арктангенс точки с координатами x = 1 и y = 1:

Результат вычисления этой формулы в MathCad будет следующий: