Что такое непериодическая функция: определение и примеры

Введение

Пропорциональные величины

Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:

y = kx,

где k — постоянная величина (коэффициент пропорциональности).

График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая

с осью X угол , тангенс которого равен k:

tg = k (рис.8).

Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = -3.

Линейная функция

Если переменные y и x связаны уравнением 1-ой степени:

где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае — нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.

Обратная пропорциональность

Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением: y = k / x, где k — постоянная величина. График обратной пропорциональности – гипербола (рис.10).

У этой кривой две ветви. Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy= k.

Основные характеристики и свойства гиперболы:

область определения функции: , область значений: ;
функция монотонная (убывающая) при x < 0 и при x > 0, но не монотонная в целом из-за точки разрыва x = 0 (подумайте, почему?);
функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая;
нулей функция не имеет.

Квадратичная функция

Это функция:

где a, b, c — постоянные, .

В простейшем случае имеем:

График этой функции квадратная парабола — кривая, проходящая через начало координат (рис.11). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.

График функции

— тоже квадратная парабола того же вида, что и , но её вершина лежит не в начале координат, а в точке с координатами:

Форма и расположение квадратной параболы в системе координат полностью зависит от двух параметров: коэффициента a при x2 и дискриминанта D.

D = b2 – 4ac.

Эти свойства следуют из анализа корней квадратного уравнения.

Основные характеристики и свойства квадратной параболы:

— область определения функции: ( т.e. ), а область значений: …

(ответьте, пожалуйста, на этот вопрос сами!);

— функция в целом не монотонна, но справа или слева от вершины ведёт себя, как монотонная;

— функция неограниченная, всюду непрерывная, чётная при b = c = 0, и непериодическая;

— при D < 0 не имеет нулей. (А что при ?).

Свойства непериодических функций

1. Отсутствие периода: Основным свойством непериодических функций является отсутствие периода. Это означает, что непериодическая функция не повторяется после некоторого фиксированного интервала времени или значения аргумента. Таким образом, для непериодической функции не существует такого значения, на котором она бы повторяла свое значение.

2. Бесконечная изменчивость: Непериодические функции могут иметь бесконечное число экстремумов, точек перегиба и других особенностей. Это связано с их непредсказуемым и разнообразным поведением на всем протяжении области определения.

3. Большой информационный потенциал: Непериодические функции содержат богатый набор информации об исследуемом явлении. Такие функции могут быть использованы для аппроксимации и моделирования различных процессов и явлений в науке, технике и других областях.

4. Сложность анализа: Из-за отсутствия периода непериодические функции сложнее анализировать и предсказывать, чем периодические. Это связано с их непостоянством и непредсказуемым поведением. Для изучения непериодических функций требуется применение сложных методов математического анализа и численных методов.

5. Уникальность каждой точки: В отличие от периодических функций, в которых значение функции в одной точке совпадает с значением в других точках, каждая точка непериодической функции является уникальной. Это делает непериодические функции более гибкими и мощными инструментами для описания сложных процессов и явлений.

Примеры непериодических функций
Функция
Описание

sin(x)
Тригонометрическая функция с изменяющейся амплитудой и периодом

exp(x)
Экспоненциальная функция с бесконечным ростом

log(x)
Логарифмическая функция с областью определения (0, +∞)

В заключение можно сказать, что непериодические функции представляют собой разнообразные и уникальные математические сущности, которые находят широкое применение в научных и практических областях

Изучение и анализ непериодических функций является важной задачей для понимания сложных процессов и явлений, а также разработки эффективных математических моделей

Иррациональные числа: определение

Иррациональное число — это число, которое невозможно представить в виде дроби m/n, где m — целое число, а n — натуральное. Это определение довольно сухое и формальное — сейчас объясним понятнее.

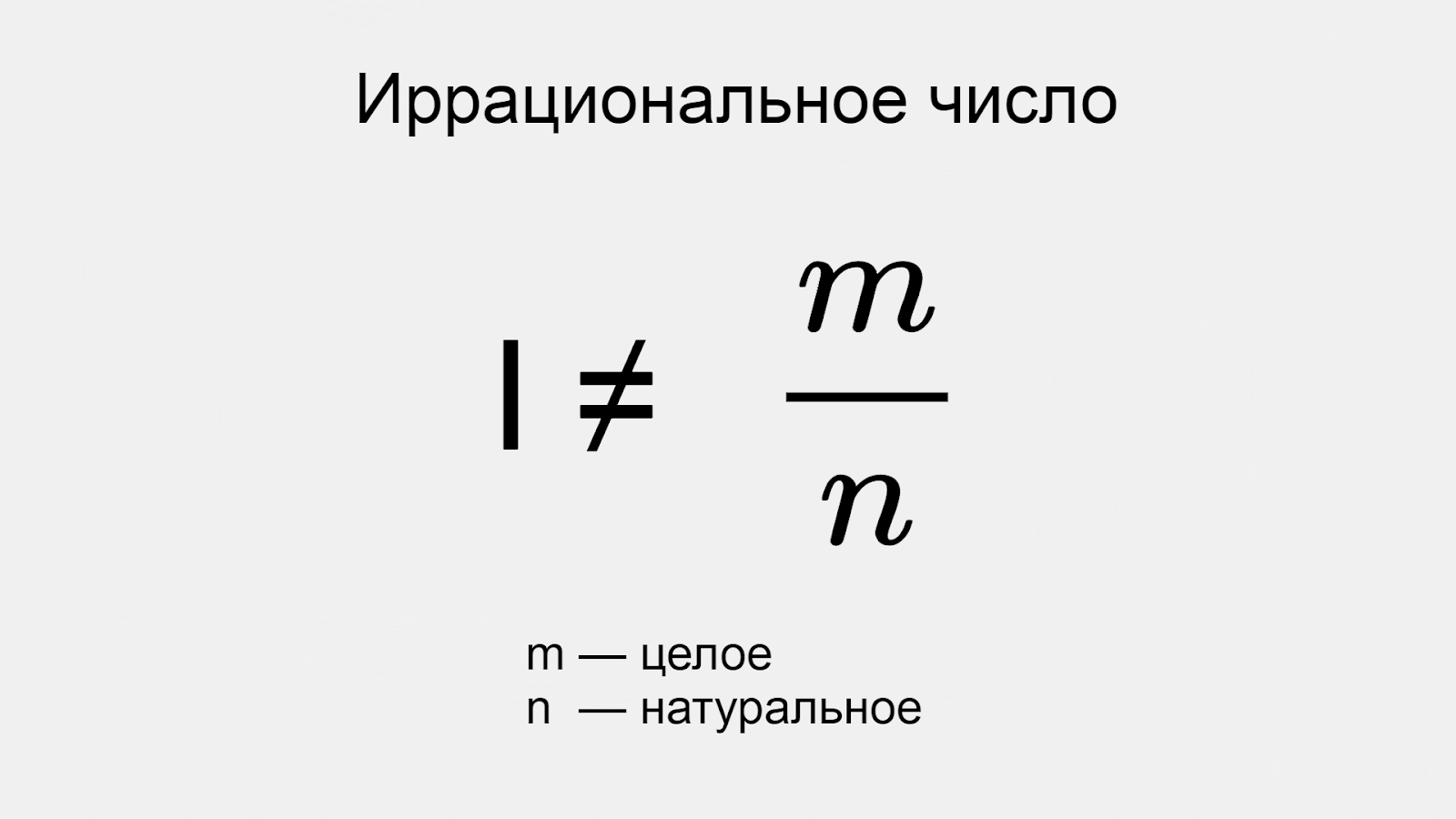
Изображение: Skillbox Media

Простыми словами, иррациональное число — это бесконечная непериодическая дробь. «Бесконечная» означает, что у дроби есть бесконечное количество цифр после запятой. «Непериодическая» — что у этих цифр нет никакой повторяющейся закономерности.

Например, число √2 — иррациональное. Если попробовать извлечь из него корень с помощью калькулятора, получится число 1,4142135623… Цифры после запятой будут высчитываться бесконечно, а в их последовательности не будет никакой логики.

Другие примеры иррациональных чисел:

Число Пи: π = 3,1415926535…
Число Эйлера: e = 2,7182818284…
Золотое сечение: φ = 1,6180339887…
√2 = 1,4142135623…
√3 = 1,7320508075…
√5 = 2,2360679774…
√7 = 2,6457513110…
√11 = 3,3166247903…

Интересный факт

Впервые иррациональное число √2 обнаружил один из учеников Пифагора, когда пытался найти гипотенузу равностороннего треугольника. Это открытие пошатнуло строгие законы математики, которая прежде считалась исключительно точной наукой. Стоит ли говорить, что бесконечные числа в это мировоззрение уж точно не вписывались.

Ещё один известный пример иррационального числа — число π (Пи). Учёные и по сей день соревнуются в попытках вычислить максимальное количество знаков после запятой у этого числа. Так, в 2022 году команда разработчиков из Google побила мировой рекорд, вычислив около 100 трлн знаков, в которых всё так же не находилось повторяющегося периода.

Так как иррациональные числа бесконечны, чисто гипотетически в нём рано или поздно можно встретить свой номер телефона, дату рождения или какую-либо закодированную информацию бесконечное количество раз.

Определение и свойства логарифмической функции

Рассмотрим следующие функции:

Показательная .
Логарифмическая .

Заметим, что данные функции являются взаимно обратными. Графики логарифмической и показательной функций симметричны по отношению к прямой y=x, которая играет роль биссектрисы первой и третьей координатных четвертей.

Логарифмическая функция обладает следующими характерными свойствами:

Область определения:
Значения соответствуют следующему множеству:
Четность/нечетность: функция относится к общему виду.
Период: функция является непериодической.
График логарифмической функции пересекает оси координат в следующих точках:

с осью абсцисс: точка A(1:0)
общие точки с осью ординат отсутствуют

Промежутки знакопостоянства:

0 < a < 1: y > 0 для и y<0 для
a > 1: y > 0для и y<0 для

Монотонность:

0<a<1: функция является убывающей для какого-либо
a>1: функция является возрастающей для какого-либо

У логарифмической функции отсутствуют точки минимума и максимума.

Понятие непрерывности функции.

Определение 1

Функция $f(x)$, определенная в некоторой окрестности точки $a$, называется непрерывной в точке $a$, если
$$
\displaystyle \lim_{x\rightarrow a}f(x)=f(a)\label{ref1}
$$

Таким образом, функция $f$ непрерывна в точке $a$, если выполнены следующие условия:

функция $f$ определена в некоторой окрестности точки $a$, то есть существует число $\delta_0>0$ такое, что $U_{\delta_{0}}(a)\subset D(f)$;
существует $\displaystyle \lim_{x\rightarrow a}f(x)=A$;
$A=f(a)$.

Определение непрерывности функции $f(x)$ в точке $a$, выраженное условием \eqref{ref1}, можно сформулировать с помощью неравенств (на языке $\varepsilon-\delta$), с помощью окрестностей и в терминах последовательностей соответственно в виде

$\forall \varepsilon>0\ \exists\delta>0:\quad\forall x:|x-a| < \delta\rightarrow|f(x)-f(a)| < \varepsilon,$
$\forall \varepsilon>0\ \exists\delta>0:\quad\forall x\in U_{\delta}(a)\rightarrow f(x)\in U_{\varepsilon}(f(a)),$
$\displaystyle\forall\{x_{n}\}:\ \lim_{n\rightarrow\infty}x_{n}=a\rightarrow\lim_{n\rightarrow\infty}f(x_{n})=f(a).$

Назовем разность $x-a$ приращением аргумента и обозначим $\Delta x$, а разность $f(x)-f(a)$ — приращением функции, соответствующим данному приращению аргумента $\Delta x$, и обозначим $\Delta y$. Таким образом,
$$
\Delta x=x-a,\;\Delta y=f(x)-f(a)=f(a+\Delta x)-f(a).\nonumber
$$

При этих обозначениях равенство \eqref{ref1} примет вид
$$
\lim_{\Delta x\rightarrow 0}\Delta y=0.\nonumber
$$

Таким образом, непрерывность функции в точке означает, что бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Пример 1

Показать, что функция $f(x)$ непрерывна в точке $a$, если:

$f(x)=x^3, a=1$;
$f(x)=\displaystyle \frac{1}{x^{2}}, a\neq 0$;
$f(x)=\sqrt{x}, a>0$;
$f(x)=\displaystyle \left\{\begin{array}{lc}x\sin\frac1x,&x\neq0,\\0,&x=0,\end{array}\right.a=0$

$\triangle$Если $x\rightarrow 1$, то по свойствам пределов (\S 10, (11)) получаем $x^3\rightarrow 1$, то есть для функции $f(x)=x^3$ в точке $x=1$ выполняется условие \eqref{ref1}. Поэтому функция $x^3$ непрерывна в точке $x=1$.
Если $x\rightarrow a$, где $a\neq 0$, то, используя свойства пределов (\S 10), получаем $\displaystyle \frac{1}{x}\rightarrow\frac{1}{a},\;\displaystyle \frac{1}{x^{2}}\rightarrow\frac{1}{a^{2}}$, то есть Функция $\displaystyle \frac{1}{x^{2}}$ непрерывна в точке $x=a,\;(a\neq 0)$.
Так как $\displaystyle |\sqrt{x}-\sqrt{a}|=\frac{|x-a|}{\sqrt{x}+\sqrt{a}}$, то отсюда получаем $0\leq|\sqrt{x}-\sqrt{a}|\;<\;\displaystyle\frac{|x-a|}{\sqrt{a}}$. Следовательно, $\sqrt{x}-\sqrt{a}\rightarrow 0$ при $x\rightarrow a$. Это означает, что функция $\sqrt{x}$ непрерывна в точке $a$, где $a>0$.
Функция $f$ определена на $\mathbb{R}$, и при любом $x\in\mathbb{R}$ выполняется неравенство $0\leq|f(x)-f(0)|=|f(x)|\leq|x|$, так как $\left|\sin{\frac{1}{x}}\right|\leq1$ при $x\neq 0$. Следовательно, $\displaystyle \lim_{x\rightarrow 0}f(x)=f(0)=0$, то есть функция $f$ непрерывна в точке $x=0.\quad\blacktriangle$

По аналогии с понятием предела слева (справа) вводится понятие непрерывности слева (справа). Если функция $f$ определена на полуинтервале $(a-\delta,a]$ и $\displaystyle \lim_{x\rightarrow a-0}f(x)=f(a)$, то есть$f(a-0)=f(a)$, то эту функцию называют непрерывной слева в точке $a$.

Аналогично, если функция $f$ определена на полуинтервале $[a,a+\delta)$ и $f(a+0)=f(a)$, то эту функцию называют непрерывной справа в точке $a$.

Например, функция $f(x)=$ непрерывна справа в точке $x=1$ и не является непрерывной слева в этой точке, так как $f(1-0)=0,\;f(1+0)=f(1)=1$.

Очевидно, функция непрерывна в данной точке тогда и только тогда, когда она непрерывна как справа, так и слева в этой точке.

Значимость непериодических чисел в математике

Непериодические числа играют важную роль в математике и имеют множество применений и свойств, которые делают их интересными и полезными.

1. Криптография:

Непериодические числа часто используются при разработке криптографических алгоритмов и систем шифрования. Это связано с их случайной и нерегулярной структурой, которая делает их трудными для предсказания и взлома. Одним из примеров является использование непериодических чисел при создании ключей для шифрования данных.

2. Фракталы:

Непериодические числа со своей неограниченной и непредсказуемой природой также являются важной основой для создания фракталов. Фракталы – это сложные и красивые геометрические фигуры, которые могут быть построены с использованием итерационных процессов, в которых применяются непериодические числа

3. Хаос:

Непериодические числа тесно связаны с понятием хаоса и динамических систем. Многие системы в природе демонстрируют хаос, который может быть описан и анализирован с использованием непериодических чисел. Для прогнозирования таких сложных процессов часто применяются математические модели, в которых используются непериодические числа.

4. Алгоритмы и случайность:

Непериодические числа играют важную роль в алгоритмах и моделировании случайных процессов. Они используются, например, при генерации случайных чисел в компьютерных программированиях и при проведении статистических исследований. Непериодические числа обеспечивают надежность случайности и позволяют получать более точные результаты в различных приложениях.

5. Математические теории:

Непериодические числа являются объектом исследования в различных математических теориях. Так, например, в теории чисел изучаются свойства и структура непериодических десятичных дробей. Исследование непериодических чисел также ведется в теории множеств, топологии и других разделах математики.

Таким образом, непериодические числа имеют широкий спектр применения и значимости в различных областях математики и приложений. Их нерегулярная и непредсказуемая структура делает их полезными для решения сложных задач, создания безопасных систем и моделирования реальных процессов.

Логарифмическая функция — что это в математике

Логарифм обозначают, как .

С помощью логарифма выполняют сложные операции в алгебре. С данным понятием можно столкнуться в разных науках. К примеру, в теории вероятностей, в генетике и физике.

Большое значение это понятие имеет в астрономии. Освещенность звезд зависит от их видимой величины. Данная зависимость также является логарифмической. Кроме того, логарифмическая шкала децибелов позволяет измерять громкость звуков.

Логарифмическая функция имеет вид: . Понятие и формулу активно используют в науке. К примеру, с помощью логарифмической функции выполняют следующие действия:

определение корней дифференциальных уравнений;
классификация значений, которыми обладают такие величины, как частота и интенсивность звука;
аппроксимация неких зависимостей;
изучение теории информации и теории вероятностей.

Свойства иррациональных чисел

У иррациональных чисел, как и у любых других, есть свои свойства. Давайте пройдёмся по каждому из них.

1. Если сложить иррациональное число с рациональным, получится иррациональное число:

π + 2 = 3,1415926535… + 2 = 5,1415926535…

√2 + 3 = 1,4142135623… + 3 = 4,4142135623…

Это же правило действует и при вычитании:

π − 3 = 3,1415926535… − 3 = 0,1415926535…

√7 − 1,645 = 2,6457513110… − 1,645 = 1,0007513110…

2. Если умножить иррациональное число на рациональное, получится иррациональное число:

π ∙ 8 = 3,1415926535… ∙ 8 = 25,1327412287…

√5 ∙ 3 = 2,2360679774… ∙ 3 = 6,7082039324…

3. Если вычесть одно иррациональное число из другого, может получиться рациональное или иррациональное число:

π − π = 3,1415926535… − 3,1415926535… = 0

√3 − √2 = 1,732050807… − 1,4142135623… = 0,3178372451…

4. При сложении или умножении двух иррациональных чисел может получиться рациональное или иррациональное число:

Примеры непериодических функций:

1. Функция единичного импульса (дельта-функция) — это функция, которая имеет значение 0 во всех точках, кроме одной, где она равна бесконечности. Такая функция является непериодической, так как не существует периода, при котором функция повторяется. Примером дельта-функции является функция ультрафиолетового облучения в точке попадания на экран.

2. Функция гауссова пуля также является примером непериодической функции. Эта функция представляет собой кривую в форме колокола, которая имеет пик в центре и затухает по мере удаления от центра. Гауссова пуля часто используется в математическом моделировании и статистике.

3. Функция ступенька Хевисайда – это функция, которая равна 0 при отрицательных значениях аргумента и равна 1 при положительных значениях аргумента. Такая функция является непериодической, так как не повторяется ни при каком периоде аргумента. Ступенька Хевисайда широко используется в системах автоматического управления и теории сигналов.

4. Функция белого шума – это функция, которая представляет собой случайную последовательность значений, в которой каждое значение равно некоторому случайному числу. Такая функция является непериодической, так как не повторяется ни при каком периоде. Белый шум широко используется в телекоммуникациях и обработке сигналов.

Примеры непериодических функций
Функция
Описание

Единичный импульс
Функция, которая имеет значение 0 во всех точках, кроме одной, где она равна бесконечности.

Гауссова пуля
Функция в форме колокола с пиком в центре и затуханием по мере удаления от центра.

Ступенька Хевисайда
Функция, которая равна 0 при отрицательных значениях аргумента и равна 1 при положительных значениях.

Белый шум
Случайная последовательность значений, в которой каждое значение равно случайному числу.

Свойства периодических функций

Периодическая функция — это такая функция, которая имеет общую особенность: ее значения повторяются через определенные промежутки. Основные свойства периодических функций:

Период функции — это такой числовой промежуток, через который функция имеет одинаковые значения. Обозначается T и может быть положительным или отрицательным.
Определение на всей числовой прямой — периодическая функция может быть определена на всей числовой прямой, то есть для любого действительного числа x. Некоторые периодические функции могут иметь ограниченный диапазон определения.
Сдвиг функции — если к периодической функции добавить константу, то график функции сдвинется вправо или влево, но останется периодическим. Например, функция f(x) = sin(x) имеет период 2π, а функция f(x) = sin(x + π/2) имеет тот же период, но график сдвинут влево на π/2.
Функция с минимальным периодом — каждая периодическая функция имеет минимальный период, через который ее значения повторяются. Минимальный период может быть найден путем нахождения наименьшего положительного значения T, для которого f(x + T) = f(x) для всех x.
Сумма и произведение периодических функций — если f(x) и g(x) — периодические функции с периодом T, то их сумма f(x) + g(x) и произведение f(x) * g(x) также являются периодическими функциями с тем же периодом T.

Понимание свойств периодических функций позволяет более глубоко исследовать и анализировать их характеристики и поведение на числовой прямой.

Что такое монотонность, как построить график

Функция является монотонной на каком-то отрезке при возрастании или убывании в определенном промежутке. Таким образом, монотонность функции определяется в виде ее однообразия.

Можно сказать, что функция возрастает при:

Условие выполняется для любых двух точек определенного интервала, которые характеризуются соотношением:

x2 > x1

Таким образом, больший аргумент соответствует большему значению функции. График при этом изображают на координатной плоскости снизу вверх.

Функция является убывающей при:

В этом случае на определенном интервале две точки характеризуются следующим соотношением:

x2 > x1

Тогда больший аргумент соответствует меньшему значению функции. Следовательно, график будет расположен сверху вниз.

Смягченными условиями для записанных формулировок являются неубывающие и невозрастающие функции. В первом случае справедливо неравенство , а во втором — . Тогда подобные функции на заданном промежутке обозначают в виде монотонности функции на интервале.

Строгая монотонность представляет собой подвид обычной монотонности. Функция является постоянной, то есть немонотонной, при условии, что для нее не характерно убывание или возрастание.

Логарифмическая функция — строго монотонна. Если основание логарифмической функции а>1, то она возрастает. Когда основание определяется, как 0<a<1, функция является убывающей.

Можно заметить, что график любой логарифмической функции пересекает точку с координатами (1; 0). Причиной этому служит справедливость равенства log 1 = 0 в случае любого основания a.

Попробуем доказать, что логарифмическая функция является монотонно возрастающей:

Запишем известные данные:

Заменим значение х во втором выражении на значение х из первого равенства и получим главное логарифмическое тождество:

Заметим, что в данном случае а>0, а≠1 и b>0. Если утверждать, что логарифмическая функция является монотонно возрастающей, то больший аргумент должен соответствовать большему значению функции:

Представим x1 и x2, используя основное логарифмическое тождество:

Значения x2 и x1отобраны в соответствии с областью определения. Они являются положительными:

В результате:

Полученное неравенство является показательным. Здесь степени обладают равными основаниями, которые больше, чем единица. Можно сделать вывод о том, что допустимо выполнить сравнение показателей при неизменном знаке неравенства:

Утверждение доказано.

Логарифмикой нередко обозначают непрерывную кривую логарифмической функции. У нее отсутствует экстремум. На графике она занимает следующие положения:

возрастает, если a>0;
убывает, если 0<a<1.

Возрастающей и убывающей логарифмической функции соответствуют следующие графики:

Заметим, что логарифмическая функция на графике в любом случае имеет точки пересечения с осью абсцисс. Точка пересечения обладает координатами: (1;0).

При работе с логарифмическими функциями важно понимать принцип оценки логарифмических констант. Рассмотрим типичный пример, где требуется оценить числа:. Функция, которая имеет основание 2, при x = 1 принимает нулевое значение

Рассмотрим какие-нибудь степени числа 2:

Функция, которая имеет основание 2, при x = 1 принимает нулевое значение. Рассмотрим какие-нибудь степени числа 2:

x = 2 (первая степень), при у=1

x = 4 (вторая степень), при у=2

x = 8 (третья степень), при у=3

Аргумент x = 7 занимает место на промежутке между x = 4 и x = 8

Тогда значение, которым обладает функция , можно определить между 2 и 3.

Аналогично рассмотрим аргумент x = 3. Он располагается между x = 2 и x = 4. Тогда функция обладает значением, которое можно отметить на промежутке между 1 и 2.

Запишем ответ:

Попробуем найти решения неравенства:

Очевидно то, что здесь требуется оценить логарифмические константы. Аналогично предыдущему примеру, начнем с первого логарифма, далее рассмотрим второй логарифм и все вместе:

В результате получается, что значение первого логарифма соответствует интервалу от 2 до 3. Второй логарифм расположен в промежутке от 3 до 4. Таким образом, разность данных логарифмов меньше нуля, либо имеет нулевое значение. При условии выполнения начального неравенства х должен быть <0, то есть отрицательным.

Можно записать краткий ответ, как .

Понятие непериодического числа

Непериодическое число — это такое десятичное дробное число, которое не может быть представлено в виде периодической десятичной дроби. Периодическая десятичная дробь имеет последовательность цифр, которая повторяется бесконечно. Например, число 1/3 имеет периодическую десятичную запись 0.3333…, где цифра 3 повторяется бесконечно.

Непериодические числа, в отличие от периодических, не имеют повторяющихся цифр или последовательностей. Они могут иметь бесконечное количество десятичных разрядов, но без повторений.

Одним из примеров непериодического числа является число π (пи). Запись числа π в десятичной системе не имеет периода и не повторяется. Его десятичное представление начинается как 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089…

Другим примером непериодического числа является число e (экспонента). Оно также не имеет периода в своем десятичном представлении и начинается как 2.7182818284590452353602874713526624977572470936999595749669676277240766303535475945…

Непериодические числа имеют важное значение в математике и широко применяются в различных областях, таких как физика, информатика и статистика. Их иррациональность и непериодичность делают их инструментом для решения сложных математических задач и моделирования реальных явлений