Квадратное число

Числа и математика: исследование разных операций

Сложение чисел – это операция, при которой два числа объединяются в одно по определенным правилам. Результатом сложения является сумма чисел, которая может быть больше или меньше исходных чисел, в зависимости от их значений.

Для исследования свойств сложения чисел можно воспользоваться таблицей:

Первое число	Второе число	Сумма
1	2	3
3	4	7
5	6	11

Как видно из таблицы, сумма двух чисел может быть больше, чем каждое из них по отдельности. Например, сумма чисел 5 и 6 равна 11, что больше, чем каждое из этих чисел. Это можно объяснить тем, что при сложении чисел происходит их объединение, а значит, получившаяся сумма будет включать в себя все элементы исходных чисел.

Важно отметить, что результат сложения чисел зависит от их значений и порядка, в котором они складываются. Поэтому, чтобы получить наибольшую сумму, нужно выбирать наибольшие числа и складывать их в определенном порядке

Также в мире математики существуют и другие операции, такие как умножение чисел. Умножение – это операция, при которой одно число увеличивается в заданное количество раз. Результатом умножения является произведение чисел.

Для изучения свойств умножения чисел также можно использовать таблицу:

Первое число	Второе число	Произведение
2	3	6
4	5	20
6	7	42

Как видно из таблицы, произведение двух чисел может быть больше или меньше исходных чисел. Например, произведение чисел 6 и 7 равно 42, что больше, чем каждое из этих чисел. Однако, произведение чисел 2 и 3 равно 6, что меньше, чем каждое из этих чисел. Возможные варианты зависят от значений исходных чисел и их порядка.

Таким образом, как сложение, так и умножение чисел имеют свои особенности и приводят к разным результатам. Однако, для определения, что больше – сумма чисел или их произведение, необходимо учитывать и другие факторы, такие как количество чисел и их значения

Поэтому, при решении задач в мире математики, важно анализировать все доступные данные и выбирать подходящую операцию для решения конкретной задачи

Виды преобразования выражений

Иррациональные выражения содержат операцию извлечения корня. Это особые записи, состоящие из радикалов и знаков алгебраических действий.

Во время преобразования таких выражений нельзя допускать сужения области допустимых значений. С ними разрешается проводить любые из основных тождественных преобразований:

раскрытие скобок;
группировка подобных множителей и слагаемых;
перестановка множителей и слагаемых;
замена разности суммой.

Замена исходной записи

Подкоренное выражение можно заменить тождественно равным, то есть математической записью, значение которой будет равно исходному. Следует учитывать, что равенство должно соблюдаться при любых допустимых значениях переменных, которые входят в состав обоих выражений.

Использование свойств корней

Для упрощения сложных выражений часто применяются свойства корней, к примеру, перемножение их степеней. Делать это необходимо в соответствии со специальными формулами.

Особое внимание при работе следует обращать на отрицательные числа и выражения с переменными. В ряде случаев для применения формул такие значения сначала придётся привести к тождественно равным, которые подойдут для дальнейшего использования свойств корней.. Внесение множителя под знак корня — это преобразование произведения, в котором лишь один из множителей находится под знаком радикала со степенью, выраженной натуральным числом

После замены выражения под корнем будут находиться все множители, составляющие произведение, но оно останется равным исходному.

Внесение множителя под знак корня — это преобразование произведения, в котором лишь один из множителей находится под знаком радикала со степенью, выраженной натуральным числом. После замены выражения под корнем будут находиться все множители, составляющие произведение, но оно останется равным исходному.

Изменение дробей

Иррациональные математические записи могут содержать дроби с радикалами в делимом или делителе. С ними разрешается проводить любые действия, относящиеся к основным преобразованиям дробных чисел:

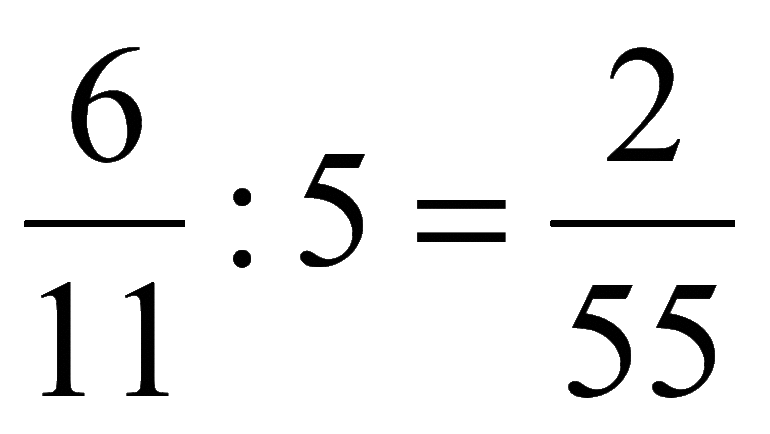
Отдельное вычисление выражений, находящихся в числителе и знаменателе.
Изменение знака перед дробью, которое влечёт за собой перемену знаков делимого и делителя.
Проведение сокращения дроби, если это является возможным и целесообразным. Зачастую перед тем как сократить значение, необходимо вычислить множители, составляющие числитель и знаменатель. Иногда перед сокращением можно заменить переменную, чтобы исходная иррациональная величина стала более удобной рациональной.
Приведение к новому знаменателю посредством умножения делимого и делителя на один дополнительный множитель. При этом действии следует учитывать, что выполнение сокращения или приведения к новому знаменателю возможно только на область допустимого значения переменных для исходного числа.

Избавление от иррациональности в знаменателе

Освобождение от иррациональности в знаменателе представляет собой преобразование дроби путём её замены на тождественно равную с делителем, не содержащим корней и степеней. Для этого необходимо последовательно провести два действия:

Умножение числителя и знаменателя на значение, которое отличается от 0.
Преобразование выражения, ставшего новым делителем.

Переход к степеням

Переход от радикалов к степеням осуществляется на основе равенства, давшего определение степени, которая имеет рациональный показатель. При этом используется следующая формула:

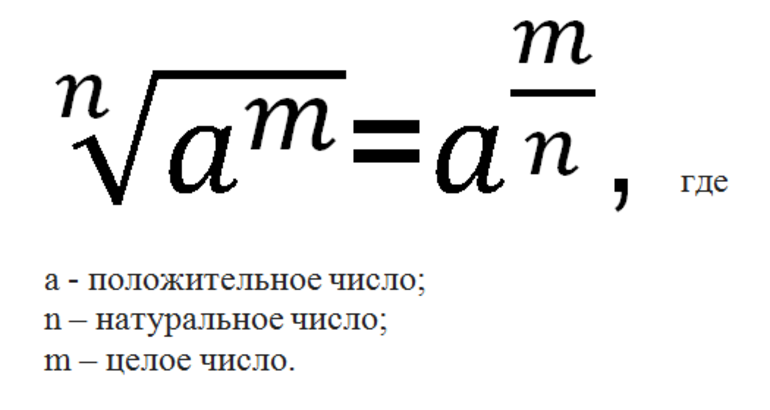
Если же величина под радикалом отрицательная или там находится выражение с переменными, то перед использованием формулы подкоренное значение необходимо преобразовать. Для этого следует применять свойства степеней.

Номер 6: Компьютерная графика и математика

Многие люди думают, что для создания компьютерной графики не нужна математика. Но это далеко не так. Графика основана на математических принципах и алгоритмах, которые позволяют создавать линии, кривые, тени, освещение и многое другое.

Пиксели и векторы. Каждый элемент графики состоит из множества пикселей – маленьких точек с определенным цветом. Для создания гладких линий и форм используются векторы – математические объекты, определяющие направление и длину линии.
Матрицы трансформации. Для изменения размера и положения объекта на экране используются матрицы трансформации – математические объекты, представляющие движение, повороты и изменение масштаба объекта.
3D-графика. Для создания трехмерной графики используются математические объекты, такие как векторы и матрицы, чтобы определить положение объекта в трехмерном пространстве, его размеры, материалы и теневые эффекты.

Таким образом, математика позволяет создавать красивую и реалистичную компьютерную графику, которая выводит нашу жизнь на новый уровень.

Самое большое число

Из школьного курса известно, что наибольшего числа не существует. Ведь если к самому большому числу прибавить хотя бы единицу, то получим еще большее число. Школьник с легкостью скажет, что, например, самое большое двузначное число — 99, а трехзначное — 999 и т.д.

Существует два алгоритма наименования чисел – английский и американский.

В американском названия больших чисел строятся следующим образом: сначала идет латинское порядковое числительное, а затем добавляется суффикс «иллион». Исключение – миллион. Далее получаются числа: триллион, квадриллион, квинтиллион. После идут секстиллион, септиллион, октиллион, нониллион и дециллион. Такой способ используют в США, Канаде, России и Франции.

Американский алгоритм наименования чисел

Английский алгоритм используют в Испании и Великобритании, а так же в ряде бывших колоний.

Здесь названия строятся так: к латинскому числительному прибавляют суффикс «иллион», к следующему числу (которое больше в 1000 раз) уже добавляют суффикс «иллиард».

После триллиона идет триллиард, после квадриллион, квадриллиард и т.д. Получается, что по английскому и американскому алгоритму одни и те же большие числа называются по-разному.

Читайте по теме: Самое маленькое число

В русский язык из английской системы пришел только миллиард (109), который американцы называют биллионом. Иногда в России употребляют слово триллиард, т.е. 1000 триллионов или квадриллион.

Самое большое простое число в мире – 274207281 – 1, которое содержит 22 338 618 десятичных цифр (простое число Мерсенна). Значение нашли в 2015 году в ходе проекта по распределенному поиску простых чисел Мерсенна GIMPS.

Поясним, что простыми называются натуральные (целые положительные) числа, имеющие только два делителя — единицу и само себя. Например, 2, 3, 5, 7 — простые числа. Список продолжают 11, 13, 17, 19… Кроме двойки все числа нечетные, иначе бы делились не только на единицу и себя, но и на два.

Значит, найденное простое число еще и самое большое из нечетных.

Маренн Марсен и самое большое простое число

По утверждению Евклида, простых чисел бесконечное множество, значит, наибольшего простого числа нет. Ученые до сих пор ищут числа-рекордсмены. И тому есть разумное объяснение. Всемирная организация Electronic Frontier Foundation учредила награды за подобные открытия: чем больше найденное число, тем выше награда.

Есть специальный способ проверки простоты чисел, который называется тест Люка-Лемера. Правда, предназначен он исключительно для чисел Мерсенна. Что же это за числа? Это вид натуральных чисел, расположенных в определенной последовательности. Имя им дал французский математик Мерсенн Марен. Вид числа Мерсенна такой:

Mn = 2n – 1,

где n — натуральное число.

При n = 1, 2, 3, 4, … числа Мерсенна образуют последовательность, начинающуюся с 1, 3, 7, 15. Затем идут 31, 63, 127. Продолжают ряд 255, 511, 1023, 2047 и т.д.

Такие числа используют в криптографии, например, для усовершенствования банковских кодов.

Внесистемные числа

Кроме чисел, которые записаны при помощи английской или американской систем, известны внесистемные числа. У них есть собственные названия, в которых нет латинских префиксов. Для понимания сначала рассмотрим запись латинскими числительными.

Единица – это 100, десять — 101 и так далее: миллиард — 109, триллион — 1012, квадриллион — 1015, квинтиллион — 1018, секстиллион — 1021, септиллион — 1024, октиллион — 1027, нониллион — 1030, дециллион — 1033.

С помощью приставок можно и дальше выводить числа: андециллион, дуодециллион, тридециллион и так далее. Но нужны собственные названия чисел, а тут только составные названия. Поэтому по этой системе собственных имен еще только три — вигинтиллион — 1063, центиллион — 10303, миллеиллион — 103003.

В миллеиллионе 3003 нуля

Число с собственным, а не составным названием больше 103003 получить невозможно. Однако числа больше миллеиллиона известны – это внесистемные числа.

Самое маленькое внесистемное число носит название мириада. Означает сотню сотен, т.е. 10000.

Что такое квадратное число?

Квадратным числом называется число, полученное путем возведения целого числа в квадрат. Иными словами, квадратное число — это число, которое получается умножением целого числа на само себя.

Например, число 9 является квадратным числом, так как оно равно 3 в квадрате: 3 * 3 = 9. Также число -9 является квадратным числом, так как (-9) * (-9) = 81.

Квадратные числа могут быть как положительными, так и отрицательными. Например, 16 и -16 — это квадратные числа, так как 4 * 4 = 16 и (-4) * (-4) = 16.

Квадратные числа имеют много применений в математике и других областях. Например, они используются в геометрии для определения площади квадратных фигур, в физике для вычисления квадратичной зависимости и в программировании для выполнения различных вычислений.

Чтобы определить, является ли число квадратным, достаточно вычислить его квадратный корень. Если результат является целым числом, то исходное число является квадратным. Например, квадратный корень из 25 равен 5, что означает, что 25 является квадратным числом.

Таблица некоторых квадратных чисел:

Число	Квадратное число
1	1
2	4
3	9
4	16
5	25
6	36
7	49
8	64
9	81
10	100

Таким образом, квадратное число — это число, которое получается путем возведения целого числа в квадрат. Они имеют множество применений и являются важным понятием в математике.

Диапазон возможных окончаний

При изучении квадратов целых чисел мы можем заметить, что окончания квадратов также являются повторяющимся паттерном. Отличие заключается только в окончании чисел. Рассмотрим различные диапазоны возможных окончаний:

Окончание 0:

Квадраты чисел, оканчивающихся на 0 также будут оканчиваться на 0. Например, 10 в квадрате равен 100.

Окончание 1:

Если число оканчивается на 1, то квадрат этого числа также будет оканчиваться на 1. Например, 11 в квадрате равен 121.

Окончание 4:

Квадраты чисел, оканчивающихся на 2 или 8, будут оканчиваться на 4. Например, 12 в квадрате равен 144.

Окончание 5:

Если число оканчивается на 5, то квадрат этого числа будет оканчиваться на 5. Например, 15 в квадрате равен 225.

Окончание 6:

Квадраты чисел, оканчивающихся на 4 или 6, будут оканчиваться на 6. Например, 14 в квадрате равен 196.

Окончание 9:

Если число оканчивается на 3 или 7, то квадрат этого числа будет оканчиваться на 9. Например, 13 в квадрате равен 169.

Других возможных окончаний для квадратов целых чисел не существует. Это связано с тем, что при возведении числа в квадрат остаток от деления этого числа на 10 не меняется. Таким образом, окончание числа и его квадратного корня будет одинаковым.

Какие еще примеры особых чисел можно привести?

Одним из наиболее известных примеров особенных чисел являются простые числа. Простым числом называется число, которое делится без остатка только на 1 и на само себя. Таким образом, первые несколько простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23 и так далее.

Еще одним примером особенных чисел являются так называемые совершенные числа. Совершенным числом называется число, которое равно сумме всех своих делителей, кроме самого числа. Например, первое совершенное число — 6 (6 = 1 + 2 + 3).

Среди особых чисел можно выделить также числа Армстронга. Число Армстронга — это число, которое равно сумме цифр своего числа, возведенных в степень, равную количеству цифр в числе. Например, число 153 — число Армстронга, так как 1^3 + 5^3 + 3^3 = 153.

Еще одним примером особенных чисел являются числа Фибоначчи. Числа Фибоначчи — это последовательность чисел, где каждое последующее число равно сумме двух предыдущих. Таким образом, первые несколько чисел Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21 и так далее.

Наконец, можно упомянуть числа Капрекара. Число Капрекара — это число, которое при возведении в квадрат и последующей записи числовых цифр в двух частях (например, при возведении числа 45 в квадрат будет получено число 2025, которое будет разбито на две части — 20 и 25) дает сумму, равную исходному числу. Примерами чисел Капрекара являются числа 1, 9, 45, 55, 99 и так далее.

Зависимость чисел от культурных и социальных факторов

Культурный контекст играет важную роль в определении числовых концепций. Например, в западной культуре число 13 считается несчастливым, в то время как в некоторых восточных культурах число 4 считается несчастливым. Культурные поверья и традиции формируют различные ассоциации и эмоциональное отношение к определенным числам.

Социальные факторы также могут влиять на восприятие чисел. Например, экономический статус человека может влиять на его отношение к деньгам и числам, связанным с богатством и бедностью. В разных обществах может существовать разная система счета, которая отражает социально-экономическую организацию и ценности этого общества.

Язык также может вносить свой вклад в восприятие чисел. Некоторые языки имеют разные слова или синтаксические конструкции для описания определенных чисел. Например, некоторые языки имеют отдельное слово для обозначения число «один» при счете объектов, а отдельное слово для обозначения «один» при измерении времени или расстояний.

Таким образом, численный язык не является универсальным и независимым от контекста. Зависимость чисел от культурных и социальных факторов подчеркивает необходимость учета различных культурных и социальных контекстов при интерпретации числовой информации.

Какие перспективы и вызовы стоят перед математикой в отношении особых чисел?

Поиск новых особых чисел. Уже существующие особые числа дают огромное количество возможностей для исследований и применений. Однако, с каждым годом математики обнаруживают новые типы особых чисел, такие, как супер-простые числа и числа Рамануджана. Поиск новых особых чисел, особенных свойств и особенностей, может открыть новые горизонты для математики и науки в целом.

Проблема сложности вычислений. Одним из вызовов, связанных с особыми числами, является сложность вычислений. Некоторые из этих чисел могут быть вычислены только с использованием специализированных алгоритмов и компьютерных программ. Иногда вычисление даже одного значения может занимать множество лет вычислительной мощности самых современных компьютеров. Эта проблема становится еще более актуальной с появлением квантовых компьютеров, которые могут изменить представление о том, что считается «вычислимым».

Применение в криптографии и других областях. Одной из сфер применения особых чисел является криптография. Некоторые типы особых чисел могут помочь создать более надежные системы шифрования, которые могут быть использованы, например, в мобильных девайсах. Кроме того, особые числа также могут находить свое применение в электронном дизайне, физике, оптике и других областях науки, таких как исследование квантовых явлений.

Десятичные числа и десятичная система счисления

Десятичная система счисления – это самая распространенная система счисления в нашей повседневной жизни. В этой системе счисления используется десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Десятичные числа состоят из цифр, где каждая цифра имеет свое место значения. Например, число 253 состоит из трех цифр: 2, 5 и 3. Цифра 2 находится на месте сотен, цифра 5 – на месте десятков, а цифра 3 – на месте единиц.

Количество мест значений в десятичном числе зависит от его длины. Например, в длинном числе 12345 количество мест значений равно пяти.

Примеры десятичных чисел:

17
249
1000
6789

В десятичной системе счисления каждая цифра имеет свое значение, определяемое ее местом в числе. Например, цифра 7 в числе 6789 находится на месте тысяч, а цифра 8 – на месте сотен.

Десятичные числа могут быть как положительными, так и отрицательными. Отрицательные числа обозначаются знаком «минус», стоящим перед числом.

Преимущества десятичной системы счисления:

Простота использования в повседневной жизни.
Большинство результатов вычислений в десятичной системе сразу понятны без дополнительных преобразований.
Возможность точного представления десятичных дробей.

Десятичная система счисления широко применяется в финансовых операциях, торговле, инженерии и других областях, где точность и понятность результатов являются важными факторами.

Цифра	Значение
ноль
1	один
2	два
3	три
4	четыре
5	пять
6	шесть
7	семь
8	восемь
9	девять

Кто считается ведущими учеными в исследовании особых чисел и какие результаты они достигли?

Среди ведущих ученых, занимающихся исследованиями в области особых чисел, можно назвать таких математиков, как Леонард Адлер, Герберт Уилф, Стэнли Эйрак и другие.

Леонард Адлер – это профессор математики в университете штата Нью-Йорк и известный теоретик чисел. Он является соавтором книги «Символический подход к теории чисел», которая рассматривает теорию вероятностей и устранение выражений.

Герберт Уилф – это профессор математики в Университете штата Филадельфия. Он является одним из основателей школы комбинаторного анализа и чьи труды являются одними из важнейших в этой области.

Стэнли Эйрак – это профессор математики в Массачусетском технологическом институте и автор ряда важных работ в области комбинаторики, теории графов и теории чисел. Он является соавтором книги «Теория и перечисление различных перестановок» и других важных работ.

Результаты их исследований позволили более глубоко изучить особенности различных типов особых чисел, а также открыть новые типы особых чисел, уточнить их свойства и упорядочить их классификацию.

Понятие самого большого числа

Мы все привыкли думать о числах как о бесконечным мире, где существует множество чисел, каждое из которых превосходит предыдущее. Но что если я скажу вам, что существует самое большое число? Звучит удивительно, правда? Но это не просто математический фокус или фантастическая идея, это настоящая концепция, которую математики изучают уже много лет.

Итак, что такое самое большое число? Когда мы говорим о самом большом числе, мы обычно подразумеваем число, которое больше любого другого числа, что просто может покоситься на наши представления о числовом пространстве. Можно сказать, что оно является вершиной над остальными числами, величайшим представителем числового мира. Но здесь надо быть осторожным, потому что в математике такое понятие, как «самое большое число», не всегда имеет смысл.

Статьи по теме вопроса

Основные понятия математики
Математика является одной из наиболее важных и фундаментальных наук, которая изучает структуру, свойства и отношения между различными объектами. Она является неотъемлемой частью нашей жизни и применяется во многих областях, таких как физика, экономика, биология и технические науки….
История развития математики
Математика – это наука, которая изучает количество, структуру, пространство и изменения. Она является одной из самых древних наук и имеет богатую и интересную историю развития.Первые шаги в математикеПервые упоминания о математике можно найти уже в древнейшей письменности,…
Роль математики в современном мире
Математика – это наука, которая изучает структуру, свойства и взаимосвязи чисел, пространства, структур и изменений. Она является одной из самых фундаментальных наук и играет огромную роль в различных областях жизни.Математика в технологияхСовременный мир невозможно представить без…
Математические методы и их применение
Математика является одной из основных наук, которая широко используется в различных областях нашей жизни. Однако, ее значение не ограничивается только теоретическими вычислениями и формулами. Математические методы имеют большое практическое применение и помогают решать сложные задачи в…
Математические теории и их значение
Математика – это наука, которая изучает структуру, пространство, количество и изменение. Она является одной из самых фундаментальных наук и имеет широкое применение в различных областях жизни – от ежедневных расчетов до сложных научных исследований. В своей основе математика использует…
Влияние математики на другие науки
Математика – это одна из старейших и наиболее важных наук, которая играет огромную роль в развитии человечества. Ее применение не ограничивается только сферой точных наук, таких как физика или химия, но также оказывает значительное влияние на другие области знаний.Развитие…
Задачи и проблемы, решаемые с помощью математики
ВведениеМатематика – это наука о числах, формулах и пространстве. Она является одной из основных наук и играет важную роль в различных областях человеческой деятельности. Многие люди могут думать, что математика не имеет никакого отношения к их повседневной жизни, но на самом деле она…
Современные достижения в области математики
Математика является одной из старейших наук и постоянно развивается, открывая новые горизонты для исследований. Сегодня мы поговорим о самых значительных достижениях в области математики за последние несколько десятилетий.Искусственный интеллект и машинное обучениеОдним из…
Интересные факты о математике
Математика — это наука, которая изучает структуру, пространство, количество и изменение. Она играет важную роль в нашей жизни, от повседневных расчетов до сложных научных и технических разработок. Но помимо своей практической значимости, математика также представляет собой увлекательное поле…
Практическое применение математики в повседневной жизни
Математика является одним из фундаментальных наук, которая изучает структуру, свойства и взаимосвязь чисел, пространства, структур и изменений. Многие люди считают ее сложной и непонятной, однако она имеет огромное практическое применение в нашей повседневной жизни.ФинансыОдно из…

Американская система

Интересным окажется тот факт, что данная система используется не только в Америке и Канаде, но и в России. К тому же она имеет и свое научное название: система именования чисел с короткой шкалой. Как же называются в данной системе большие числа? Так, секрет довольно-таки простой. В самом начале будет идти латинское порядковое числительное, после же просто добавится всем известный суффикс «-иллион». Интересным окажется следующий факт: в переводе с латинского языка число «миллион» можно перевести как «тысячища». Американской системе принадлежат следующие числа: триллион — это 10 12 , квинтиллион — 10 18 , октиллион — 10 27 и т. д. Несложно будет также разобраться, сколько же нулей записано в числе. Для этого нужно знать

простую формулу

: 3*х + 3 (где «х» в формуле — это латинское числительное).

Задача по математике — 3764

ГЛАВНАЯ » РЕШЕБНИК

2019-06-16 Будем называть $2n$-значное число особым, если око само является точным квадратом, и числа, образованные его первыми цифрами и его последними $n$ цифрами, также являются точными квадратами (при этом второе $n$-значное число может начинаться с цифры 0, но не должно быть равно нулю, а первое не может начинаться с нуля).
а) Найдите все двузначные и четырехзначные особые числа.
б) Возможны ли шестизначные особые числа? (Докажите, что их нет или приведите пример такого числа,)
в) Докажите, что существует хотя бы одно 20-значное особое число.
г) Докажите, что существует не более 10 особых 100-значных чисел.
д) Докажите, что существует хотя бы одно 30-значное особое число.

Решение:а) Пусть $(10x + t)^2 = 100x^2 + 20xt + t^2$, где $20xt + t^2$ — квадрат натурального числа, меньшего 10, $x$ и $t$ — целые числа от 1 до 9 и $x^2 >10$. Тогда $x \geq 4$ и $x \leq 4$, что возможно лишь при $x = 4$ и $t = 1$.
Ответ: существует одно двузначное 49 и одно четырехзначное $1681 = 41^2$ особое число.
б) Ответ: да; например, $256036 = 506^2$.
в) Чтобы получить нужное особое число вида
$(10^5 x + 1)^2 = 10^{10}x^2 + 2 \cdot 10^5 x + 1$,
достаточно найти целое $x$ такое, что $10^9
$(4999900001)^2 = 24999000019999800001$;
оно «состоит» из $49999^2$ и $99999^2$).
г) Для любого $k$ особым $4k$-значным числом может быть лишь
$(10^kx + t)^2 = 10^2kx^2 + 2 \cdot 10^k xt + t^2$
при $10^{2k-1} \leq x^2 3 \cdot 10^{k-1}$, и $6 \cdot 10^{2k-1} t
(1) $u + 1$ делится на $5 \cdot 10^{k-1}$;
(2) $u$ делится на $2^{к-1}$, $u + 1$ — на $5^k$;
(3) $u$ делится на $5^k$, $u + 1$ — на $2^{k-1}$.
Каждый случай дает не более чем одно решение, удовлетворяющее условию $u
Более детальные рассуждения показывают, что таких чисел не более двух.
д) Для любого $k$ существует по крайней мере одно $(4k + 2)$-значное особое число, а именно $z^2 = v + w^2$, где $v = 25 \cdot 10^{2k-1}, w$ — наименьшее натуральное число, большее $\sqrt v$. Пусть $у = w^2 — v$; при этом $z^2 = 4v \cdot w^2 + y^2 = 10^{2k+1} w^2 + у^2$ «состоит» из $w^2$ и $y^2$ и будет особым, если выполнены неравенства $0
Поскольку $w — 1
В частности, с помощью компьютера можно найти, при $k = 7$, число
$z = 25 \cdot 10^{13} + 15811389^2 = 500000022109321$,
квадрат которого — 30-значное особое число. Полнее исследование в задаче о $(4k + 2)$-значных особых числах, связанное с десятичным разложением числа $\sqrt{10}$, представляется довольно безнадежным и не слишком интересным.

Правило отсчета: цифра десятков меньше цифры единицы

Для определения количества двузначных чисел, удовлетворяющих условию, что цифра десятков меньше цифры единицы, используется правило отсчета. Это правило позволяет составить все возможные комбинации двух различных цифр и узнать их количество.

Для начала, рассмотрим, сколько существует возможных цифр для каждого разряда. В десятичной системе исчисления каждое число может принимать значения от 0 до 9, включительно. Значит, для цифры десятков у нас есть 9 вариантов выбора (от 1 до 9), а для цифры единиц — также 9 (от 0 до 9 без учета уже выбранной цифры десятков).

Теперь можем применить правило отсчета. Для каждого возможного значения цифры десятков (9 вариантов) у нас есть по 9 вариантов выбора цифры единиц. Таким образом, общее количество двузначных чисел, удовлетворяющих условию, можно определить, умножив 9 на 9.

Таким образом, получаем, что существует 81 двузначное число, где цифра десятков меньше цифры единицы.

Простые выводы

Итак, какое самое большое число сегодня? На

данный момент

найдено оно американским ученым из университета Миссури Кертисом Купером, которое можно записать следующим образом: 2 57885161 — 1. При этом оно также является 48 числом французского математика Мерсенна. Но стоит сказать о том, что конца в этих поисках быть не может. И неудивительно, если через определенное время ученые нам предоставят на рассмотрение следующее новонайденное самое большое в мире число. Можно не сомневаться, что произойдет это в самые ближайшие сроки.

Бесчисленное множество различных чисел окружает нас каждый день. Наверняка многие люди хотя бы раз интересовались, какое число считается самым большим. Ребенку можно просто сказать, что это – миллион, но взрослые прекрасно понимают, что за миллионом следуют и другие числа. Например, стоит только каждый раз прибавлять к числу единичку, и оно будет становиться все больше – так происходит до бесконечности. Но если разобрать числа, имеющие названия, то можно узнать, как называется самое большое число в мире.