Количество прямых, проходящих через три точки

Геометрия своими словами для детей

Геометрия – это часть математики, которая изучает пространственные отношения и фигуры. Она помогает нам измерять и описывать различные формы и объекты вокруг нас.

В геометрии мы учимся работать с разными фигурами, такими как круги, треугольники, прямоугольники и т.д. Мы узнаем, как отличать их друг от друга, а также как вычислять их свойства, такие как площадь и периметр.

Например, мы можем узнать, что круг имеет форму, похожую на колесо, и все его точки равноудалены от центра. Мы также можем научиться вычислять его площадь и длину окружности.

Треугольник имеет три стороны и три угла. Мы можем изучить различные виды треугольников, такие как равносторонний треугольник, у которого все стороны и углы равны, или прямоугольный треугольник, у которого один из углов равен 90 градусам.

Прямоугольник имеет четыре стороны, противоположные стороны параллельны, и все углы равны 90 градусам. Мы можем изучить, как вычислить его площадь и периметр.

Геометрия также помогает нам разбираться с пространственными отношениями, такими как расстояние между двумя точками или угол между двумя линиями.

Изучение геометрии может быть очень интересным и полезным. Оно помогает нам понимать мир вокруг нас и использовать математические концепции для решения различных задач.

Используемая литература:1. Белова, Т.И. Вычисление неопределенных интегралов. Обыкновенные дифференциальные уравнения. Компьютерный курс: учеб. пособие / Т.И.Белова, А.А.Грешилов, И.В.Дубограй; Ред. А.А.Грешилов. — М.: Логос, 2004. — 184 с. + 1 эл. опт. диск (CD-ROM).2. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. — 22-е изд., перераб. — СПб.: Профессия, 2006. — 432 с.3. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. — 22-е изд., перераб. — СПб.: Профессия, 2005. — 432 с.4. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. для вузов. В 2 ч. Ч.1 / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий. — 4-е изд., стереотип. — М.: Дрофа, 2004. — 725 с.5. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч. 1. Дифференциальное и интегральное исчисление / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; Ред. В.А.Садовничий. — 3-е изд., испр. — М.: ДРОФА, 2001. — 725 с.6. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч.2. Ряды, несобственные интегралы, ряды Фурье, преобразование Фурье / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; ред. В.А.Садовничий . — 3-е изд., испр. — М.: ДРОФА, 2001. — 712 с.7. Голоскоков, Д.П. Уравнения математической физики. Решение задач в системе Maple: учеб. для вузов / Д.П.Голоскоков. — СПб.: Питер, 2004. — 538с.8. Гурова, З.И. Математический анализ. Начальный курс с примерами и задачами: учеб. для втузов / З.И.Гурова, С.Н.Каролинская, А.П.Осипова; Ред. А.И.Кибзун. — М.: Физматлит, 2002. — 351 с.9. Лукьянов, А.В. Обыкновенные дифференциальные уравнения: учеб. пособие по решению задач / А.В.Лукьянов, Ю.Д.Погуляев. — Челябинск: Полиграф-Мастер, 2006.10. Математический анализ в вопросах и задачах: учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, Г.Н.Медведев, А.А.Шишкин; Ред. В.Ф.Бутузов . — 5-е изд., испр. — М.: ФИЗМАТЛИТ, 2002. — 479 с.Значение термина Геометрия  на academic.ru

Функциональное применение геометрии в нашей жизни.

Геометрия – это наука о пространственной форме, размерах и относительном расположении объектов. Она играет важную роль в нашей жизни, ведь без использования геометрии невозможно представить себе многие сферы деятельности, начиная от архитектуры и дизайна и заканчивая техническими науками.

Архитектура – одна из областей, где геометрия существенно влияет на результат. Архитекторы используют принципы геометрии, чтобы создать красивые, эргономические и стабильные здания. Они определяют форму и размеры всех элементов здания, начиная с основания и заканчивая крышей. Для создания качественной и безопасной конструкции необходимо учесть все аспекты геометрии, начиная от расположения отдельных элементов здания и заканчивая расположением окон и дверей.

Дизайн также невозможен без геометрии. Дизайнеры используют геометрические принципы, чтобы создать привлекательный и эстетичный дизайн. Геометрия помогает здесь определить размеры и пропорции объектов, которые будут использованы в дизайне, включая формы, геометрические фигуры, линии и текстуры.

Кроме того, геометрия играет важную роль в инженерных и технических науках. В этих областях геометрия используется для проектирования и создания машин, устройств, инструментов и технологических наладок. Различные формы и геометрические фигуры используются для создания точных и эффективных деталей, необходимых для производства тех или иных устройств. Если бы не геометрия, то эти устройства и машины были бы неэффективными, а часто и просто невозможными для создания.

Одна из важных областей применения геометрии – это также картография. Эту науку волнует проблема описания и изображения географических объектов на картах. Они могут быть представлены в различных проекциях и в различном масштабе, а для этого требуются знания в геометрии.

Другая важная область, использующая геометрию – это небольшая группа наук, изучающих движение, как например, механика. Движение предметов в трехмерном пространстве в значительной степени определяется с помощью геометрических расчетов. Эти расчеты используются для определения скорости и положения объектов, а также их ускорения и действия внешних сил на них.

В медицине геометрия также играет важную роль. На основе геометрических принципов создаются модели человеческих тканей, что позволяет лучше понимать как они работают. Это, в свою очередь, помогает лучше понимать механизмы различных болезней и разрабатывать эффективные методы лечения.

Таким образом, геометрия, казалось бы, абстрактная наука, оказывается крайне применимой во многих областях нашей жизни. От архитектуры и дизайна до медицины и производства – геометрия повсюду. Без нее мы жили бы в менее качественном мире, так как геометрия – это основа любой точной и эффективной работы.

Эллипс и его свойства

Эллипс – это геометрическая фигура, которая получается пересечением плоскости и конуса, если плоскость не проходит через вершину конуса.

Если взять две оси, одну большую и одну меньшую, то эллипс будет выглядеть как овал, причем центр овала совпадает с центром эллипса.

У эллипса есть ряд свойств, которые помогают описать его положение и размеры:

• Фокусы – точки, через которые проходят оси эллипса. Если провести линию от одного фокуса до любой точки эллипса и продолжить ее до пересечения с другой осью, то расстояние от точки пересечения до второго фокуса будет равно расстоянию от этой точки до первого фокуса.
• Большая и меньшая полуоси – это половина большей и меньшей оси, соответственно.
• Эксцентриситет – это число, которое характеризует степень сжатия эллипса относительно его формы. Чем выше эксцентриситет, тем более овальной будет форма эллипса.

Эллипс имеет много применений, от геометрии и физики до создания красивых дизайнов. Его свойства используются в проектировании спутниковых орбит, определении траекторий космических кораблей, строительстве зданий и мостов, а также в дизайне создания эстетических форм для скульптур и других произведений искусства.

Определение и основные характеристики

Основные характеристики прямой включают:

1. Бесконечность: прямая не имеет начала или конца и распространяется в обе стороны бесконечно.
2. Прямое направление: прямая простирается в одном направлении без изгибов или поворотов.
3. Единство: на любой прямой линии можно выбрать две любые различные точки, и все остальные точки на прямой линии лежат между этими двумя точками.
4. Отсутствие ширины и толщины: прямая линия имеет нулевую ширину и толщину, она представляет собой идеально тонкую линию без объема.

Примеры:

— Нить, которую мы растягиваем между двумя точками;

— Луч света, который движется в прямом направлении;

— Грани куба или параллелограмма, которые являются прямыми линиями.

Геометрическое определение

Прямая представляет собой наиболее простой элементарный объект в геометрии. Ее основная особенность заключается в том, что прямая имеет одну и только одну прямую между любыми двумя ее точками. Это означает, что прямая также является кратчайшим расстоянием между двумя точками в геометрии.

Прямая может располагаться в плоскости или в трехмерном пространстве. В плоскости она представляет собой прямую линию, которая не имеет ширины или толщины. В трехмерном пространстве прямая представляет собой объект без объема.

Примеры прямых могут включать границы сторон геометрических фигур, таких как треугольник или квадрат. Они также могут быть видимыми линиями на рисунке или шкале. В реальном мире мы можем наблюдать прямые на дорогах, равномерно отрезанных сторонах зданий или линиях на спортивных полях.

Геометрическое определение прямой является основой для понимания многих других понятий в геометрии, таких как отрезки, углы, окружности и многое другое. Оно является ключевым элементом в изучении геометрии и находит применение в различных областях науки и техники.

Алгебраическое определение

Ax + By + C = 0

где A, B и C — константы, а x и y — переменные. Такое уравнение называется уравнением прямой в общем виде.

Коэффициенты A и B определяют наклон прямой, а коэффициент C — расстояние от начала координат до прямой.

Например, уравнение 2x + 3y — 6 = 0 задает прямую, проходящую через точку (3, 0) и (0, 2).

Алгебраическое определение позволяет выразить прямую в виде уравнения, что упрощает анализ прямой и позволяет решать задачи, связанные с ее свойствами и взаимодействием с другими объектами в пространстве.

Конус и его свойства

Конус — это геометрическая фигура, образованная плоскостью, проходящей через замкнутую кривую (основание) и точку вне этой плоскости (вершину). Прямая, проходящая через вершину конуса и перпендикулярная плоскости основания, называется осью конуса.

Конус имеет несколько свойств:

• Объем конуса вычисляется по формуле: V = 1/3πr²h, где r — радиус основания, а h — высота конуса.
• Площадь боковой поверхности конуса равна Sб = πrl, где l — образующая (расстояние от вершины до точки на окружности основания, расположенной на одной из биссектрис угла наклона боковой стороны конуса).
• Величина угла между боковой поверхностью и плоскостью основания равна углу наклона боковой стороны.

Конус используется в производстве различных предметов, в том числе в качестве основы для мороженого, для изготовления шляп и в науке, например, в изучении гидродинамики жидкости в конусе.

История

Этот раздел представляет собой отрывок из «Истории геометрии» .

Геометрия как одно из свободных искусств и Евклид .

Геометрия — одна из древнейших наук . Первоначально он представлял собой совокупность практических знаний о длинах , площадях и объемах .

Вавилонская цивилизация была одной из первых культур, включивших изучение геометрии. Изобретение колеса открыло путь к изучению окружности , а затем и к открытию числа π (пи); Они также разработали шестидесятеричную систему , зная, что в каждом году 365 дней, они также внедрили формулу для вычисления площади прямоугольной трапеции . ]

В Древнем Египте оно было высоко развито, согласно текстам Геродота , Страбона и Диодора Сицилийского . Евклид , в 3 веке до н.э. C. сформулировал геометрию аксиоматическим и конструктивным образом , трактовка, которая установила норму, которой нужно следовать на протяжении многих веков: евклидова геометрия , описанная в «Элементах» .

Изучение астрономии и картографии , пытающееся определить положение звезд и планет на небесной сфере, более тысячелетия служило важным источником решения геометрических задач. Рене Декарт одновременно разработал алгебру уравнений и аналитическую геометрию , отметив новый этап, когда геометрические фигуры, такие как плоские кривые, могли быть представлены аналитически, то есть с помощью функций и уравнений. Геометрия обогащается изучением внутренней структуры геометрических объектов, проанализированных Эйлером и Гауссом , что привело к созданию топологии и дифференциальной геометрии .

Неравенства в геометрии: типы и примеры

Неравенства в геометрии играют важную роль при решении различных задач, связанных с геометрическими фигурами. Они позволяют устанавливать отношения между различными сторонами, углами или площадями фигур, а также находить ограничения для размеров геометрических объектов.

Существует несколько типов неравенств в геометрии, которые рассматриваются при решении задач:

• Неравенства между сторонами треугольника. Эти неравенства основаны на неравенстве треугольника, которое утверждает, что сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. Например, для треугольника со сторонами a, b и c справедливы следующие неравенства: a + b > c, a + c > b, b + c > a. Эти неравенства позволяют проверять, может ли заданный набор сторон образовать треугольник.
• Неравенства между углами треугольника. Углы треугольника могут быть разного размера и между ними могут существовать различные отношения. Например, неравенство треугольника утверждает, что сумма всех углов треугольника равна 180 градусов. Также в треугольнике может выполняться неравенство, согласно которому наибольший угол треугольника всегда противоположен наибольшей стороне, а наименьший угол — наименьшей стороне.
• Неравенства площадей фигур. Площади геометрических фигур могут иметь различные значения и между ними также могут существовать неравенства. Например, для двух треугольников с одной общей стороной можно установить неравенство: площадь первого треугольника меньше площади второго треугольника.

Неравенства в геометрии используются для доказательства теорем, нахождения соотношений между различными параметрами геометрических объектов, а также для решения задач, связанных с конструированием фигур или определением их свойств.

Примеры неравенств в геометрии:
Тип неравенства
Пример

Неравенство между сторонами треугольника
Для треугольника со сторонами 4, 5 и 10 верно: 4 + 5 > 10, 4 + 10 > 5, 5 + 10 > 4

Неравенство между углами треугольника
В прямоугольном треугольнике гипотенуза всегда больше каждого из катетов

Неравенство площадей фигур
Площадь круга меньше площади квадрата, описанного вокруг него

Какая геометрическая интерпретация имеет уравнение прямой в координатной плоскости?

Уравнение прямой в координатной плоскости имеет геометрическую интерпретацию, которая позволяет наглядно представить прямую и ее свойства. В координатной плоскости прямая представляет собой множество точек, удовлетворяющих заданному уравнению. Прямая образуется движением точки, которая движется параллельно самой себе.

Уравнение прямой вида y = mx + c, где m — наклон прямой, а c — координата пересечения прямой с осью ординат, обладает следующими геометрическими характеристиками:

1. Наклон прямой m задает угол наклона прямой относительно оси абсцисс. Если nаклон положителен, то прямая наклонена вправо, а если наклон отрицателен, то прямая наклонена влево. Наклон равен нулю соответствует горизонтальной прямой, а бесконечному наклону — вертикальной прямой.

2. Координата пересечения прямой с осью ординат c определяет точку, в которой прямая пересекает вертикальную ось. Если c положительно, то прямая пересекает ось ординат выше начала координат, а если c отрицательно, то прямая пересекает ось ординат ниже начала координат. Если c равняется нулю, то прямая проходит через начало координат.

Таким образом, уравнение прямой является мощным инструментом для представления и анализа прямых в координатной плоскости, позволяя определить их наклон и положение относительно осей координат.

Преподавание и изучение геометрии

Изучение геометрии включает в себя развитие визуальных и аргументационных навыков.

Чтобы изучение геометрии не было бессмысленным, важно, чтобы преподавательская группа занималась поиском баланса между связью навыков визуализации и аргументации, поскольку оба навыка необходимы в индивидуальном учебном процессе. Другими словами, речь идет не только о преподавании содержания как «рецепта» или о соблюдении того, что предусмотрено в учебной программе, но и о том, что при обучении геометрии учащийся учится логически мыслить

]

Человек с детства создает представления об окружающем его физическом мире. Они порождают потребность (теоретическую и практическую) в достижении понимания этого мира. Правое полушарие мозга оказывается наиболее полезным при наличии зрительных стимулов, в отличие от левого полушария, отвечающего за развитие вербальных навыков. Изучение геометрии вносит значительный вклад в развитие этих пространственных потребностей визуализации; однако до недавнего исторического периода, начиная с 1950-х годов, преподаватели математики заинтересовались изучением этой области, связав математические способности с пространственными способностями. ]

Относительно трудностей, которые возникают у школьников при изучении геометрии, таковы: решение задачи алгебраически; вычисляют периметры, площади и объемы, потому что они не определяют, какую формулу применить, и трудности в интерпретации того, что говорит проблема. При выполнении анализа по уровням видно, что в диверсифицированном цикле (десятый и одиннадцатый годы) основная трудность, которую они представляют, заключается в интерпретации того, о чем говорит задача. Основная трудность учащихся седьмого, восьмого и девятого курсов состоит соответственно в том, чтобы понять формулы периметра, площади и объема и усвоить определения; решать проблемную ситуацию алгебраически и с трудом извлекать информацию из геометрического чертежа. ]

Литература[править | править код]

• Комацу, Мацуо. Многообразие геометрии. — М. : Знание, 1981.
• Левитин, К. Е. Геометрическая рапсодия. — 3-е изд., перераб. и доп. — М. : ИД «Камерон», 2004. — 216 с. — ISBN 5-9594-0023-5.
• Шаль, Мишель. Исторический обзор происхождения и развития геометрических методов : в 2 т.. — М. : М. Катков, 1883.
• Граве Д. А. Геометрия // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• Геометрия // Газлифт — Гоголево. — М. : Советская энциклопедия, 1971. — ( :  / гл. ред. А. М. Прохоров ; 1969—1978, т. 6).
• История математики : в 3 т. / под ред. А. П. Юшкевича. — М. : Наука, 1970. — Т. I : С древнейших времён до начала Нового времени.
• История математики : в 3 т. / под ред. А. П. Юшкевича. — М. : Наука, 1970. — Т. II : Математика XVII столетия.
• История математики : в 3 т. / под ред. А. П. Юшкевича. — М. : Наука, 1972. — Т. III : Математика XVIII столетия.

Теоретико-групповые принципы геометрии[править | править код]

В 1872 году немецкий учёный Ф. Клейн в своей лекции, получившее в дальнейшем название «Эрлангенская программа Клейна», сформулировал общие принципы геометрии. Их смысл состоит в том, что каждая геометрия имеет своим предметом те и только те свойства фигур, которые инвариантны относительно какой-либо определённой группы преобразований. В этом смысле каждую геометрию следует называть геометрией данной группы преобразований. Существует очень много различныый геометрий: они порождаются различными группами и множествами, в которых эти группы действуют.

Если на одном и том же множестве X, подмножества которого мы будем называть фигурами, дейcтвует группа преобразований G и её подгруппа G′G’, то геометрия группы G будет менее богата фактами, нежели геометрия группы G′G’, так как чем больше преобразований содержит группа, тем меньше остаётся фактов, инвариантных относительно этих преобразований. Но при этом геометрия более широкой группы состоит из «более устойчивых» фактов, присущих более обширным классам эквивалентности, и потому более глубоких.

Приведём пример. Рассмотрим три группы, действующих на евклидовой плоскости: группу движений D, подобий M и аффинных преобразований A. Каждая из трёх групп в этом ряду является подгруппой следующей: D⊂M⊂AD \subset M\subset A . В геометрии группы D (евклидовой геометрии) все треугольники разбиваются на классы равных между собой треугольников, в геометрии группы M — на более широкие классы подобных треугольниов, а в геометрии группы A (аффинной геометрии) все треугольники эквивалентны (то есть образуют один класс). В геометрии группы D имеет место теорема Пифагора a²+b²=c², где a и b — катеты, а c — гипотенуза прямоугольного треугольника. В геометрии группы M эта теорема, записанная в виде (ac)2+(bc)2=1\left ( \frac{a}{c} \right )^2+\left ( \frac{b}{c} \right )^2=1, тоже имеет место, так как при преобразовании подобия отношение отрезков и величина углов сохраняется, в геометрии группы A понятия прямоугольного треугольника нет. Понятие высоты есть в геометрии групп D и M, понятие медианы и центра тяжести есть в геометрии всех трёх групп.

Как вычислить максимальное количество прямых, проходящих через три точки?

Для определения максимального количества прямых, проходящих через три точки, необходимо учесть основные свойства и правила геометрии. Приведем подробное объяснение этого процесса.

1. В начале, выберите три точки из приведенного набора и обозначьте их латинскими буквами, например, A, B и C.
2. Затем, постройте все возможные прямые, которые можно получить, соединяя эти три точки. Необходимо учесть, что прямую можно провести через любые две точки.
3. Если прямые, построенные в предыдущем шаге, пересекаются в одной точке, то полученный вариант будет уникальным и не пересекается с другими прямыми.
4. Если две или более прямых, которые проходят через три точки, пересекаются, то можно утверждать, что максимальное количество прямых, проходящих через эти три точки, равно количеству пересечений этих прямых.
5. Если ни одна из прямых не пересекается с другими прямыми, то максимальное количество прямых, проходящих через эти три точки, будет равно одному.

Теперь рассмотрим несколько примеров.

Пример 1:

Пусть даны три точки: A(1, 1), B(2, 3) и C(3, 5).

Мы строим три возможные прямые: AB, AC и BC. В данном случае, ни одна из прямых не пересекается с другими, поэтому максимальное количество прямых, проходящих через эти три точки, будет равно одному.

Пример 2:

Пусть даны три точки: A(0, 0), B(1, 1) и C(2, 2).

Мы строим три возможные прямые: AB, AC и BC. В данном случае, все три прямые AB, AC и BC пересекаются в точке (1, 1). Поэтому в этом случае максимальное количество прямых, проходящих через эти три точки, будет равно трем.

Таким образом, правильное вычисление максимального количества прямых, проходящих через три заданные точки, поможет нам получить решение в зависимости от их взаимного расположения.

Полезные инструменты для работы с прямыми

При работе с прямыми на плоскости могут понадобиться различные инструменты для анализа и визуализации. Вот некоторые из них:

• Графические калькуляторы или программы для построения и настройки прямых. Такие инструменты позволяют наглядно представить прямую на плоскости и проводить различные операции — от определения уравнений прямых до нахождения пересечений или углов между ними.
• Математические пакеты программирования, такие как MATLAB, Python с библиотеками NumPy или Wolfram Mathematica. Они предоставляют более мощные инструменты для работы с прямыми, включая возможность нахождения параметров прямых по заданным точкам, углов между прямыми и другие математические операции.
• Геометрические пособия, такие как чертежные инструменты и угольники, которые позволяют проводить прямые на бумаге или другой поверхности. Это полезно при изучении и практическом применении геометрии, особенно для школьников и студентов.
• Электронные таблицы, такие как Excel или Google Sheets, которые позволяют проводить вычисления и анализировать данные, связанные с прямыми. Это может быть полезно при работе с большим количеством точек или при построении графиков зависимости.

Независимо от выбранного инструмента, важно хорошо понимать основные принципы работы с прямыми и уметь применять их в реальных задачах. Используя соответствующие инструменты, можно существенно упростить и ускорить решение задач, связанных с прямыми на плоскости

Предмет геометрии[править | править код]

Конические сечения: круг, эллипс, парабола, гипербола

Геометрия занимается взаимным расположением тел, которое выражается в прикосновении или прилегании друг к другу, расположением «между», «внутри» и так далее; величиной тел, то есть понятиями о равенстве тел, «больше» или «меньше»; а также преобразованиями тел. Геометрическое тело представляет собой абстракцию ещё со времён Евклида, который полагал, что «линия есть длина без ширины», «поверхность есть то, что имеет длину и ширину». Точка представляет собой абстракцию, связанную с неограниченным уменьшением всех размеров тела, или пределом бесконечного деления. Расположение, размеры и преобразования геометрических фигур определяются пространственными отношениями.

Исследуя реальные предметы, геометрия рассматривает только их форму и взаимное расположение, отвлекаясь от других свойств предметов, таких как плотность, вес, цвет. Это позволяет перейти от пространственных отношений между реальными объектами к любым отношениям и формам, возникающим при рассмотрении однородных объектов, и сходным с пространственными. В частности, геометрия позволяет рассматривать расстояния между функциями.

Геометрические фигуры

Базовыми фигурами в геометрии на плоскости являются треугольник, четырёхугольник, многоугольник, окружность. В пространстве — это призма, пирамида, сфера, конус.

«Треугольник» — простейшая фигура в геометрии, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих вершины треугольника. Отрезки при этом будут называться сторонами треугольника. У треугольника три угла и три стороны. Поэтому можно выделить прямоугольные треугольники (один из углов — прямой), остроугольные треугольники (все углы — острые), тупоугольные треугольники (если один угол тупой). Замечательным свойством треугольника будет формула о сумме его углов, которая равна 180°. Иными словами, если α, β, γ — углы треугольника, то верно равенство α + β + γ =180°.

Треугольник ABC

Если классифицировать треугольники с позиции сторон, то треугольники делятся на равносторонние (все стороны равны), равнобедренные (две стороны из трех равны, но не равны третьей) и произвольные.
В треугольник против наибольшего угла лежит наибольшая сторона и наоборот.
Огромное значение треугольники играют в геометрии благодаря тому, что почти любая фигура разбивается на треугольники каким-либо методом. Таким образом, чтобы уметь анализировать более сложные фигуры, нужно знать свойства треугольника.

Базовое значение в геометрии играет теорема Пифагора, которая гласит, что в любом прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов. a2+b2=c2{\displaystyle a^{2}+b^{2}=c^{2}} Для решения большинства задач в геометрии так или иначе используются теорема Пифагора.

«Четырёхугольник» — фигура, состоящая из четырёх вершин и четырёх отрезков, последовательно соединяющих его вершины, являющихся его сторонами, при этом никакие три вершины не лежат на одной прямой. Последнее требование позволяет исключить вырожденные четырёхугольники, которые представляют собой треугольники или прямые. Важными представителями четырёхугольников являются параллелограмм и трапеция, поскольку почти все остальные четырёхугольники можно анализировать на основе их свойств.

• Параллелограмм — четырёхугольник, у которого противоположные стороны попарно равны и параллельны.
• Трапеция — четырёхугольник, у которого две противоположные стороны параллельны и две другие не параллельны.

Наиболее популярными четырёхугольниками на практике являются квадраты, прямоугольники и ромбы, которые уже определяются на основе параллелограммов.

• Ромб — четырёхугольник, у которого все стороны равны.
• Прямоугольник — четырёхугольник, у которого все углы прямые.
• Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны.

Сфера с радиусом r и диаметром d

Любой многоугольник уже разбивается на вышеописанные фигуры, поэтому его свойства можно изучать на основе рассмотренных фигур. Особняком стоит окружность или круг. Введение понятие «окружности» или «равноудалённости» значительно расширяет функционал и угол зрения геометрической науки. В свою очередь широкое применение круга на практике заставляет геометров пристально изучать свойства окружности, чтобы найденные таким образом закономерности инженеры могли применить в промышленности и других практических областях.

Окружность — это множество точек одной плоскости, равноудаленных от одной точки (центра окружности). При этом расстояние от любой точки окружности до её центра называется радиусом окружности или круга. Термин круг используется, если требуется включить все точки внутри окружности в одну фигуру. Отсюда следует, что окружность в отличие от круга не имеет площади. Но окружность является границей круга.

Если в определении окружности убрать требование на нахождение точек в одной плоскости, то получится сфера или шар.

• Сфера — это множество точек пространства, равноудаленных от одной точки (центра сферы). Сфера является границей шара.
• Призма — многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Эти параллелограммы называются боковыми гранями призмы, а оставшиеся два многоугольника называются её верхними и нижними основаниями. Наиболее популярной призмой является куб.
• Пирамида — многогранник, основанием которого является многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.
• Конус — геометрическая фигура в пространстве, образованная множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса).

Вопрос-ответ:

Какие бывают геометрические фигуры?

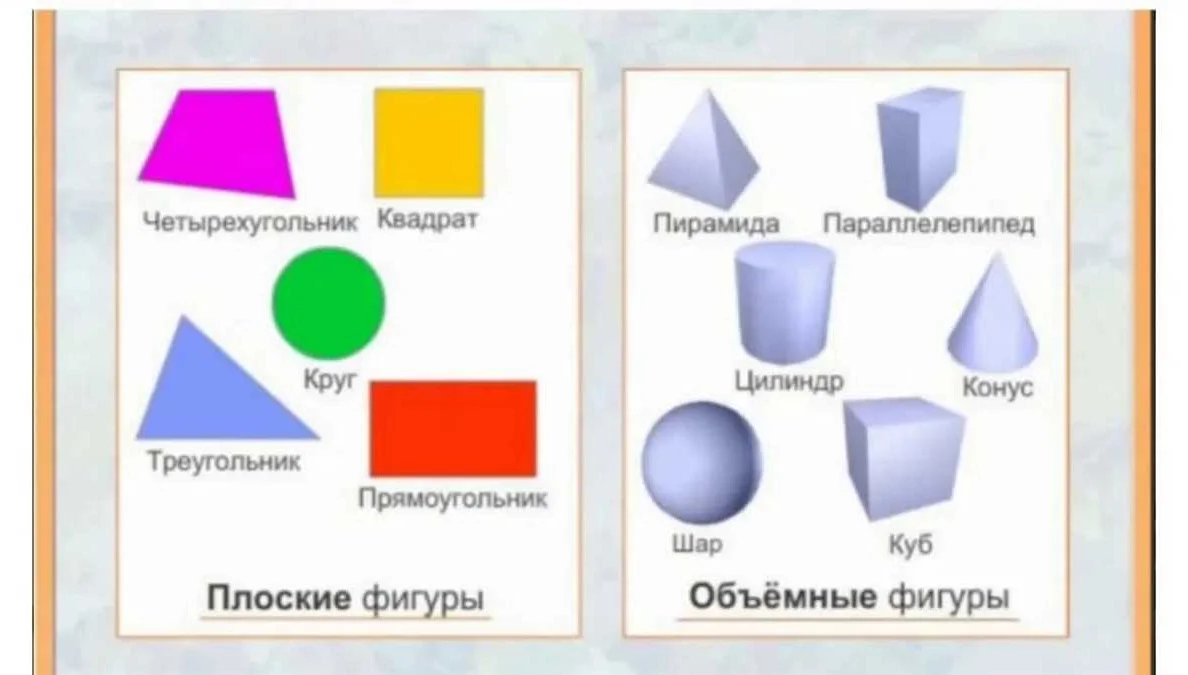
В геометрии выделяют две группы фигур: плоские и пространственные. К плоским относятся: точка, прямая, отрезок, луч, угол, треугольник, четырехугольник, многоугольник, круг, эллипс и параллелограмм. А к пространственным – пирамида, призма, куб, параллелепипед, цилиндр и конус.

Как найти периметр и площадь фигуры?

Для нахождения периметра фигуры нужно сложить длины всех его сторон. Для нахождения площади нужно умножить длину на ширину. Например, для круга площадь можно найти по формуле S=πr², а периметр по формуле P=2πr.

Каковы свойства треугольников?

У треугольников есть несколько свойств, например: сумма трех углов равна 180 градусам, большая сторона лежит напротив большего угла, площадь треугольника можно найти по формуле S = 1/2 * a * h, где a — основание, h — высота.

Как понять, что фигура является правильной?

Правильная фигура – это фигура, у которой все стороны и углы равны между собой. Например, правильный треугольник имеет углы 60 градусов, правильный четырехугольник — 90 градусов, а правильный пятиугольник — 108 градусов.

Как вычислить диагональ прямоугольника?

Для вычисления диагонали прямоугольника необходимо использовать теорему Пифагора. Если a и b — длины сторон прямоугольника, то диагональ вычисляется по формуле √(a² + b²).

Каковы основные формулы для вычисления площади геометрических фигур?

Основные формулы для вычисления площадей фигур: площадь круга S=πr², площадь треугольника S=1/2*ah, площадь прямоугольника S=ab, площадь трапеции S=(a+b)/2*h и площадь параллелограмма S=ah.

Роль неравенств в геометрии

В геометрии неравенства играют значительную роль, помогая определить отношения между числами, углами, сторонами и другими объектами. Использование неравенств в геометрии позволяет анализировать и сравнивать различные параметры фигур, решать задачи на нахождение пересечений и угловых отношений.

Неравенства в геометрии могут использоваться для доказательства теорем и утверждений. Они позволяют установить границы для значений величин, что позволяет выявить особенности и свойства геометрических объектов

Например, неравенство треугольника, которое утверждает, что сумма длин любых двух сторон треугольника всегда больше длины третьей стороны, является важной основой для проведения множества геометрических доказательств и построений

Неравенства также широко используются для решения задач на определение существования и свойств геометрических фигур. Например, для определения возможности построения треугольника по заданным сторонам можно использовать неравенство треугольника, а для определения свойств прямоугольника можно использовать неравенства между сторонами и углами.

Кроме того, неравенства могут быть использованы для определения отношений и свойств фигур внутри одного и того же пространства. Например, неравенства между площадями или объемами геометрических объектов позволяют сравнивать и анализировать их характеристики.

В целом, неравенства в геометрии позволяют более точно описывать и анализировать геометрические объекты и являются важным инструментом для решения задач и доказательства теорем в этой области. Они позволяют установить границы и отношения между различными параметрами фигур, а также сравнивать и анализировать их свойства.