Символы вероятности и статистики
| Символ | Название символа | Значение / определение | пример |
|---|---|---|---|
| P ( А ) | функция вероятности | вероятность события A | P ( A ) = 0,5 |
| P ( A ⋂ B ) | вероятность пересечения событий | вероятность того, что событий A и B | P ( A ⋂ B ) = 0,5 |
| P ( A ⋃ B ) | вероятность объединения событий | вероятность того, что событий A или B | P ( A ⋃ B ) = 0,5 |
| P ( A | B ) | функция условной вероятности | вероятность события A данное событие B произошло | P ( A | B ) = 0,3 |
| f ( x ) | функция плотности вероятности (pdf) | P ( a ≤ x ≤ b ) = ∫ f ( x ) dx | |
| F ( х ) | кумулятивная функция распределения (cdf) | F ( х ) = Р ( Х ≤ х ) | |
| μ | Средняя численность населения | среднее значение совокупности | μ = 10 |
| E ( X ) | ожидаемое значение | ожидаемое значение случайной величины X | E ( X ) = 10 |
| E ( X | Y ) | условное ожидание | ожидаемое значение случайной величины X с учетом Y | E ( X | Y = 2 ) = 5 |
| var ( X ) | отклонение | дисперсия случайной величины X | var ( X ) = 4 |
| σ 2 | отклонение | дисперсия значений совокупности | σ 2 = 4 |
| std ( X ) | стандартное отклонение | стандартное отклонение случайной величины X | std ( X ) = 2 |
| σ X | стандартное отклонение | значение стандартного отклонения случайной величины X | σ X = 2 |
| медиана | среднее значение случайной величины x | ||
| cov ( X , Y ) | ковариация | ковариация случайных величин X и Y | cov ( X, Y ) = 4 |
| корр ( X , Y ) | корреляция | корреляция случайных величин X и Y | корр ( X, Y ) = 0,6 |
| ρ X , Y | корреляция | корреляция случайных величин X и Y | ρ X , Y = 0,6 |
| ∑ | суммирование | суммирование — сумма всех значений в диапазоне ряда | |
| ∑∑ | двойное суммирование | двойное суммирование | |
| Пн | Режим | значение, которое чаще всего встречается в популяции | |
| MR | средний диапазон | MR = ( x макс + x мин ) / 2 | |
| Мкр | медиана выборки | половина населения ниже этого значения | |
| Q 1 | нижний / первый квартиль | 25% населения ниже этого значения | |
| 2 квартал | медиана / второй квартиль | 50% населения ниже этого значения = медиана выборки | |
| 3 квартал | верхний / третий квартиль | 75% населения ниже этого значения | |
| х | выборочное среднее | среднее / среднее арифметическое | х = (2 + 5 + 9) / 3 = 5,333 |
| с 2 | выборочная дисперсия | оценщик дисперсии выборки населения | s 2 = 4 |
| с | стандартное отклонение выборки | Оценка стандартного отклонения выборки населения | s = 2 |
| z x | стандартная оценка | z x = ( x — x ) / s x | |
| X ~ | распределение X | распределение случайной величины X | X ~ N (0,3) |
| N ( μ , σ 2 ) | нормальное распределение | гауссово распределение | X ~ N (0,3) |
| U ( а , б ) | равномерное распределение | равная вероятность в диапазоне a, b | Х ~ U (0,3) |
| ехр (λ) | экспоненциальное распределение | f ( x ) = λe — λx , x ≥0 | |
| гамма ( c , λ) | гамма-распределение | f ( x ) = λ cx c-1 e — λx / Γ ( c ), x ≥0 | |
| χ 2 ( к ) | распределение хи-квадрат | f ( x ) = x k / 2-1 e — x / 2 / (2 k / 2 Γ ( k / 2)) | |
| F ( k 1 , k 2 ) | F распределение | ||
| Корзина ( n , p ) | биномиальное распределение | f ( k ) = n C k p k (1 -p ) nk | |
| Пуассон (λ) | распределение Пуассона | е ( К ) знак равно λ К е — λ / К ! | |
| Геом ( p ) | геометрическое распределение | f ( k ) = p (1 -p ) k | |
| HG ( N , K , n ) | гипергеометрическое распределение | ||
| Берн ( p ) | Распределение Бернулли |
Как работает Cdot?
Сdot — это платформа, основанная на технологии блокчейн, которая предназначена для обеспечения безопасности и прозрачности финансовых операций. Она использует доказательство участия (Proof of Stake) для обеспечения консенсуса и достоверности данных.
Главными принципами работы Cdot являются:
- Децентрализация: Cdot предоставляет возможность участникам сети принимать активное участие в принятии решений, распределении ресурсов и обеспечении безопасности.
- Консенсус: Сdot использует механизм доказательства участия, чтобы обеспечить максимальную защиту от взлома и манипуляций данными.
- Смарт-контракты: Cdot позволяет создавать и выполнять умные контракты, что упрощает автоматизацию финансовых операций и устраняет необходимость в посредниках.
Преимущества Cdot:
- Скорость и масштабируемость: Cdot может обрабатывать большое количество транзакций в секунду, что делает платформу быстрой и готовой к масштабированию.
- Безопасность: Блокчейн Cdot обеспечивает высокий уровень безопасности, благодаря использованию криптографических алгоритмов и децентрализованной структуре.
- Прозрачность: Все транзакции в сети Cdot записываются в блокчейн, что делает их публично доступными и невозможными для изменения.
- Экономическая эффективность: Использование Cdot позволяет снизить затраты на проведение финансовых операций, устранить необходимость в посредниках и обеспечить низкие комиссии.
В целом, Cdot представляет собой инновационную платформу, которая изменяет схемы проведения финансовых операций и повышает их безопасность и эффективность.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если < 0, корней нет — ничего считать не надо.
Первое уравнение:2 − 2 − 3 = 0 ⇒ = 1; = −2; = −3; = (−2)2 − 4 · 1 · (−3) = 16.
> 0 ⇒ уравнение имеет два корня. Найдем их:
![]()
Второе уравнение:15 − 2 − 2 = 0 ⇒ = −1; = −2; = 15; = (−2)2 − 4 · (−1) · 15 = 64.
> 0 ⇒ уравнение снова имеет два корня. Найдем их
\
Наконец, третье уравнение:2 + 12 + 36 = 0 ⇒ a = 1; b = 12; c = 36;D = 122 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
\
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Множество символов в математических записях
Одним из основных символов, используемых в математических записях, является числовое множество символов. Оно включает в себя цифры от 0 до 9, а также десятичную запятую (или точку), которая обозначает разделитель десятичной части числа. Например, число 3,14 состоит из символов 3, 1, 4 и запятой.
Другие важные символы в математике — это символы операций. Эти символы используются для обозначения математических операций, таких как сложение (+), вычитание (-), умножение (× или *), деление (÷ или /) и возведение в степень (^). Например, выражение 2+3 означает сложение чисел 2 и 3.
Кроме того, в математических записях используются символы для обозначения переменных или неизвестных значений. Обычно используются буквы из латинского или греческого алфавита, такие как x, y, z, α, β, γ и т.д. Эти символы позволяют обозначать неизвестные значения и использовать их в уравнениях и формулах. Например, уравнение x + 2 = 5 обозначает, что значение переменной x равно 3.
Также в математических записях используются символы для обозначения специальных функций и операторов, таких как синус (sin), косинус (cos), тангенс (tan), логарифм (log) и др. Эти символы позволяют более точно описывать математические процессы и операции.
Все эти символы вместе образуют множество символов, используемых в математических записях. Знание и понимание этих символов позволяет математикам и научным работникам точно и ясно выражать свои идеи и решения проблем, используя язык математики.
Запись иррациональных чисел с помощью квадратного корня
А теперь попробуй решить такое уравнение \( {{x}^{2}}=3\).
Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?
Начнем с самого начала – с нуля: \( {{0}^{2}}=0\) – не подходит.
Двигаемся дальше \( \displaystyle x=1\); \( \displaystyle {{1}^{2}}=1\) – меньше трех, тоже отметаем.
А что если \( \displaystyle x=2\)?
Проверим: \( \displaystyle {{2}^{2}}=4\) – тоже не подходит, т.к. это больше трех.
С отрицательными числами получится такая же история.
И что же теперь делать? Неужели перебор нам ничего не дал?
Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между \( \displaystyle 1\) и \( \displaystyle 2\), а также между \( \displaystyle -2\) и \( \displaystyle -1\).
Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными.
И что дальше?
Давай построим график функции \( \displaystyle y={{x}^{2}}\) и отметим на нем решения.
Попробуем обмануть систему и получить ответ с помощью калькулятора (как мы это делали в начале)!
Извлечем корень из \( \displaystyle 3\), делов-то!
Ой-ой-ой, выходит, что \( \sqrt{3}=1,732050807568\ldots \) Такое число никогда не кончается.
Как же такое запомнить, ведь на экзамене калькулятора не будет!?
Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение. \( \sqrt{3}\) и \( -\sqrt{3}\) уже сами по себе ответы.
Определение и основные принципы
Cdot (Constraint/Domain Oriented Technology) — это методология разработки программного обеспечения, которая базируется на использовании ограничений и доменных моделей для создания высококачественного и легко поддерживаемого кода.
Главным принципом Cdot является выделение и явное определение ограничений при проектировании системы. Ограничения могут включать в себя требования к вводу данных, ограничения на значения переменных, контроль последовательности операций и другое.
Основные принципы Cdot включают:
Применение методологии Cdot позволяет создавать более надежное и гибкое программное обеспечение путем акцентирования внимания на ограничениях и доменных моделях. Это позволяет снизить количество ошибок, обеспечить более простое тестирование и поддержку кода, а также улучшить взаимодействие с заказчиком и пользователями системы.
Примеры решения и формулы
Перейдем от теории к практике. Приведем основные формулы и рассмотрим конкретные примеры.
Формулы для вычисления углов
Косинус угла между прямыми равен косинусу угла между их направляющими векторами:
Формула 1
\(\cos\alpha=\frac{\overrightarrow{s_1}\cdot\overrightarrow{s_2}}{\left|\overrightarrow{s_1}\right|\cdot\left|\overrightarrow{s_2}\right|}=\frac{m_1\cdot m_2+r_1\cdot r_2+p_1\cdot p_2}{\sqrt{m_1^2+r_1^2+p_1^2}\cdot\sqrt{m_2^2+r_2^2+p_2^2}}\)
Синус угла между прямой и плоскостью равен синусу угла между направляющим вектором прямой и нормальным вектором плоскости:
Формула 2
\(\sin\alpha=\frac{\vert\overrightarrow s\cdot\overrightarrow n\vert}{\left|\overrightarrow s\right|\cdot\left|\overrightarrow n\right|}=\frac{\vert m\cdot A+r\cdot B+p\cdot C\vert}{\sqrt{m^2+r^2+p^2}\cdot\sqrt{A^2+B^2+C^2}}\)
Косинус угла между плоскостями равен косинусу угла между их нормалями:
Формула 3
\(\cos\alpha=\frac{\overrightarrow{n_1}\cdot\overrightarrow{n_2}}{\left|\overrightarrow{n_1}\right|\cdot\left|\overrightarrow{n_2}\right|}=\frac{A_1\cdot A_2+B_1\cdot B_2+C_1\cdot C_2}{\sqrt{A_1^2+B_1^2+C_1^2}\cdot\sqrt{A_2^2+B_2^2+C_2^2}}\)
Пример 2
Найти угол между прямой, заданной уравнением \(\frac{x-2}5=\frac{y-1}2=\frac z3\), и плоскостью, заданной уравнением \(-x+3y+4z=0\).
Решение
Угол между прямой и плоскостью равен углу между направляющим вектором прямой и нормалью плоскости. Направляющий вектор прямой — \(\overrightarrow s\;(5;\;2;\;3)\), нормаль к плоскости — \(\overrightarrow n\;(-1;\;3;\;4)\). Тогда синус угла между прямой и плоскостью вычисляется по формуле: \(\sin\alpha=\frac{\vert\overrightarrow s\cdot\overrightarrow n\vert}{\left|\overrightarrow s\right|\cdot\left|\overrightarrow n\right|}=\frac{\left|5\cdot(-1)+2\cdot3+3\cdot4\right|}{\sqrt{25+4+9}\cdot\sqrt{1+9+16}}=\frac{13}{\sqrt{988}}\).
Ответ: \(\sin\alpha=\frac{13}{\sqrt{988}}\).
Формулы расстояний
Расстояние от точки \(N\;(x_0;\;y_0;\;z_0)\) до плоскости определяют как длину перпендикуляра к плоскости, опущенного из заданной точки:
Формула 4
\(d=\left|\frac{Ax_0+By_0+Cz_0+D}{\sqrt{A^2+B^2+C^2}}\right|\)
Расстояние от точки \(N\;(x_0;\;y_0;\;z_0)\) до прямой, заданной уравнением \(Ax+By+C=0\):
Формула 5
\(d=\left|\frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}\right|\)
Расстояние между скрещивающимися прямыми равно длине отрезка, проходящего через точку \(N\;(x_1,\;y_1,\;z_1)\), принадлежащую первой прямой, и точку \(M\;(x_2,\;y_2,\;z_2)\), принадлежащую второй прямой. Тогда расстояние между скрещивающимися прямыми вычисляется через смешанное произведение направляющих векторов \(\overrightarrow{s_1}\) и \(\overrightarrow{s_2}\) и вектора \(\overrightarrow{MN}\):
Формула 6
\(d=\frac{\left|(\overrightarrow{s_1}\times\overrightarrow{s_2})\cdot\overrightarrow{MN}\right|}{\left|\overrightarrow{s_1}\times\overrightarrow{s_2}\right|}\)
Примечание 1
Решение смешанного произведения векторов не рассматривается в рамках школьного курса алгебры и геометрии.
Примечание 2
Расстояние между двумя плоскостями можно также вычислить по расстоянию между скрещивающимися прямыми. Для этого на каждой из плоскостей задают прямую, затем вычисляют расстояние между прямыми, которое будет равно расстоянию между плоскостями.
Счетные и несчетные множества
Если между элементами двух групп можно установить взаимное немногозначное соответствие, то эти группы чисел равномощны, при условии равного количества элементов.
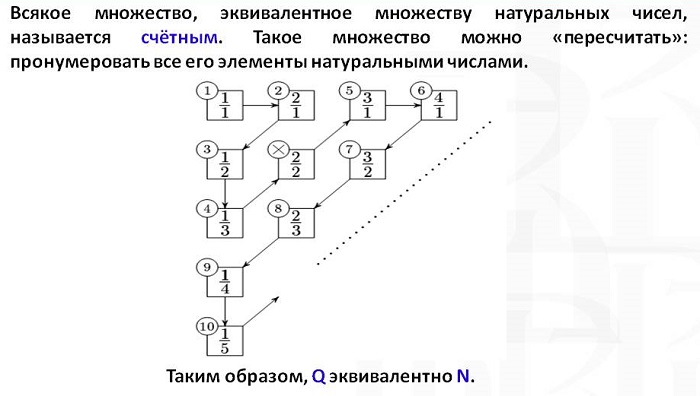
Мощность данной математической единицы равна количеству элементов в ней. Например, множество всех нечетных положительных чисел равномощно группе всех четных чисел больше ста.

Но не все группы действительных чисел счетные. Примером несчетной группы предметов является бесконечная десятичная дробь.
§1. Множества и операции над ними

Объяснение и обоснование
В курсах алгебры и алгебры и начал математического анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.
Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество М состоит из чисел 1; 2; 3, то его обозначают так: М = . Тот факт, что число 2 входит в это множество (является элементом данного множества М), записывается с помощью специального значка ∈ следующим образом: 2 ∈ М; а то, что число 5 не входит в это множество (не является элементом данного множества), записывается так: 5 ∉ М.
Можно рассматривать также множество, не содержащее ни одного элемента, — пустое множество.
Например: множество простых делителей числа 1 — пустое множество.
Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом ∅, множество всех натуральных чисел — буквой N, множество всех целых чисел — буквой Z, множество всех рациональных чисел — буквой Q, а множество всех действительных чисел — буквой R.
Множества бывают конечными и бесконечными в зависимости от того, какое количество элементов они содержат. Так, множества А = и M = — конечные, потому что содержат конечное число элементов, а множества N, Z, Q, R — бесконечные.
Множества задают или с помощью перечисления их элементов (это можно сделать только для конечных множеств), или с помощью описания, когда задается правило (характеристическое свойство), которое позволяет определить, принадлежит или нет данный объект рассматриваемому множеству. Например, А = (множество задано перечислением элементов), B — множество всех четных целых чисел (множество задано характеристическим свойством всех элементов множества). Последнее множество иногда записывают так: B = или так: B = ∈ Z> — здесь после вертикальной черточки записано характеристическое свойство*.
В общем виде запись множества с помощью характеристического свойства можно обозначить так: A = , где P (x) — характеристическое свойство. Например, = , ∈ R и x2 + 1 = 0> = ∅.
Два множества называются равными, если каждый элемент первого множества является элементом второго множества и, наоборот, каждый элемент второго множества является элементом первого множества.
Из приведенного определения равенства множеств следует, что в множестве одинаковые элементы не различаются. Действительно, например, = , поскольку каждый элемент первого множества (1 или 2) является элементом второго множества и, наоборот, каждый элемент второго множества (1 или 2) является элементом первого. Поэтому, записывая множество, чаще всего каждый его элемент записывают только один раз.
Если каждый элемент множества A является элементом множества B, то говорят, что множество A является подмножеством множества B.
Это записывают следующим образом: A ⊂ B.
Например, ⊂ , N ⊂ Z (поскольку любое натуральное число — целое), Z ⊂ Q (поскольку любое целое число — рациональное), Q ⊂ R (поскольку любое рациональное число — действительное).
Полагают, что всегда ∅ ⊆ A, то есть пустое множество является подмножеством любого множества.
Иногда вместо записи A ⊂ B используется также запись A ⊆ B.
Сопоставим определение равенства множеств с определением подмножества. Если множества А и В равны, то: 1) каждый элемент множества А является элементом множества В, следовательно, А — подмножество В (A ⊆ B); 2) каждый элемент множества В является элементом множества А, следовательно, В — подмножество А (B ⊆ A). Таким образом,
два множества равны тогда и только тогда, когда каждое из них является подмножеством другого.
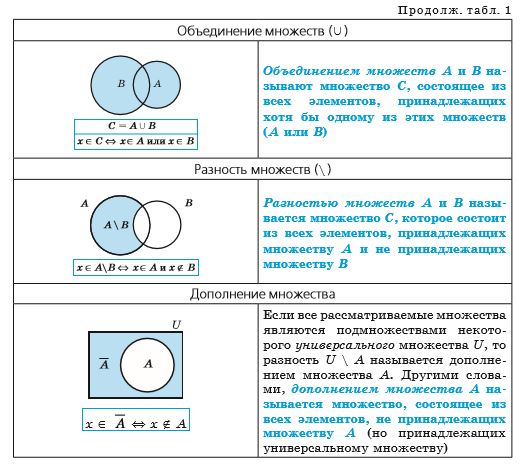
![]()
Иногда соотношения между множествами удобно иллюстрировать с помощью кругов (которые часто называют кругами Эйлера–Венна). Например, рисунок 1 иллюстрирует определение подмножества, а рисунок 2 — отношения между множествами N, Z, Q, R.
Значение символа в физике: основные формулы и их интерпретация
Физика является одной из фундаментальных наук, которая изучает природу и ее основные законы. В физике широко используются символы, которые обозначают величины и их взаимосвязь в формулах. Понимание значения символов помогает разобраться в физических законах и принципах.
Вот несколько основных символов и соответствующих им формул в физике:
-
Ф — символ силы. Сила является векторной величиной и измеряется в ньютонах (Н). Она определяет воздействие на тело, способное изменить его движение. Формула для силы: Ф = масса x ускорение.
-
а — символ ускорения. Ускорение также является векторной величиной и измеряется в метрах в секунду в квадрате (м/с²). Ускорение описывает изменение скорости объекта со временем. Формула для ускорения: а = изменение скорости / время.
-
v — символ скорости. Скорость является векторной величиной и измеряется в метрах в секунду (м/с). Скорость определяет изменение позиции объекта со временем. Формула для скорости: v = путь / время.
-
м — символ массы. Масса измеряется в килограммах (кг) и представляет собой меру инертности тела. Масса объекта влияет на его движение и взаимодействие с другими объектами. Формула для массы: м = плотность x объем.
-
т — символ времени. Время измеряется в секундах (с) и представляет собой меру изменения состояния объекта со временем. Время используется для описания длительности процессов и явлений. Формула для времени: т = путь / скорость.
Это лишь несколько примеров символов и формул, которые широко используются в физике. Понимание их значения и взаимосвязей позволяет лучше понять физические законы и принципы, а также применять их для решения задач и анализа физических явлений.
R — действительные числа
Действительные числа включают в себя все рациональные и иррациональные числа. Рациональные числа — это числа, которые могут быть представлены в виде обыкновенной или десятичной дроби, такие как 1/2 или 0.75. Иррациональные числа — это числа, которые не могут быть представлены в виде дроби, например, √2 или π.
Для обозначения действительных чисел используется символ R. Если число принадлежит множеству действительных чисел, то оно обозначается символом ∈ (принадлежит). Например, если нужно решить задачу, в которой требуется найти все действительные корни уравнения, то решение можно записать в виде x ∈ R. Это значит, что x является действительным числом.
О формулах в целом
по этой ссылкеталмуд со специальными символами$\alpha$, $\gamma$ или $\delta$. Основные математические символы тоже должны быть в вашей интегрированной среде, такие как столь любимые физиками приближённые равенства $\approx$ или интегралы с суммами.
Быстрый старт — набор простых формул
$f(x) = a\cdot x + b$
\begin{equation}\label{eq:fourierrow}
f(x) = \frac{A_0}{2} + \sum\limits_{n=1}^{\infty} A_n \cos\left( \frac{2 n \pi x}{\nu} - \alpha_n \right)
\end{equation}
\begin{equation}\label{ссылка} … \end{equation
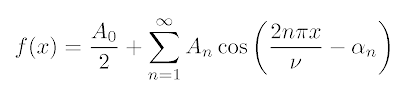
\ref{ссылка}) чтобы на неё сослаться. Имена ссылкам стоит давать на латиннице, во избежание проблем. Если формула приводится для пояснений и ссылаться на неё не надо, следует поставить после equation звёздочку, то есть equation* и после этого номер для данной формулы генерироваться не будет. Ссылки должны быть осмысленными и безошибочно говорить автору текста, какая формула имеется в виду. Не стоит потворствовать лени и глупости, проявляющихся в ссылках типа \label{uravnenie6} — следует спросить себя, что означает эта формула и дать ей осмысленное имя.
Вставка формул в текст
$ $, внутри которого помещаем формулу. Окружение $ $ переводит LaTeX в математический режим и будет отрисовывать формулы. Например: $\alpha_0$ даст нам греческую букву АЛЬФА с индексом 0. Подчёркиванием в LaTeX делается нижний индекс, и использовать подчёркивание в тексте нельзя (для подчеркивания в тексте есть пакет расширений ulem). Если хотите набирать длинные пассажи в подчёркивании — ставьте фигурные скобки $x_{i,j}$.Кроме того, ЛаТеХ категорически против двойного нижнего индекса, и команда $x_j_k$$x_{j_k}$. Если же вам нужен верхний индекс в формуле, используем символ ^ так: $x^2$. LaTeX возведёт в степень только первый символ после крышки, и если в степень нужно возвести сразу много символов, экранируем их фигурными скобками (они не отображаются в тексте): $x^{2x+1}$.Если же вы хотите набрать в формуле фигурные скобки, следует заэкранировать их вот так:\{ и они будут отрисованы в формуле, например $x \{j \}$ .
О символах в LaTeX
под названием symbols-a4.pdf Если вы обрабатываете изображения, вам пригодится команда \times, что позволяет набирать вставки типа NхM в более приглядном виде $N\times M$. А если нужно набрать в LaTeX символ градуса, можно воспользоваться таким трюком: $180^\circ$, что наберёт 180 градусов. Символ «Принадлежит» в Latex это $\in$, а символ «Любой» в это $\forall$. $\mathcal{F} {g(x,y)}$ наберёт большую и красивую букву F для фурье-преобразования.Набор скобок в LaTeX немного замороченный на первый взгляд. Можно просто поставить обычные скобки, но если формула большая, то можно поставить большие скобки в LaTeX командой $\Bigr($ и $\Bigl)$.\big\Big \bigg\Bigg
Detexify
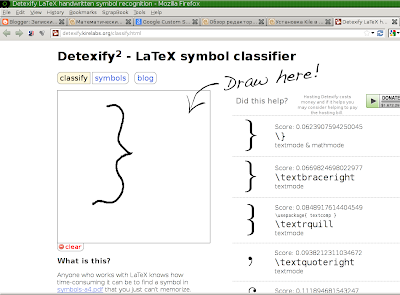
буквально то, что вы попросите. Поэтому не бойтесь в коде документа перемежать текст вставками математического режима — такой слегка костылявый способ приведёт вас к желаемому результату быстро и просто. Несколько дней практики, и вы будете рубить формулы в LaTeX, как Чапай белогвардейцев.
Извлечение квадратного корня из большого числа
Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.
Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:
- Определить «сотни», между которыми оно стоит.
- Определить «десятки», между которыми оно стоит.
- Определить последнюю цифру в этом числе.
Извлечь корень из большого числа можно разными способами — вот один из них.
Извлечем корень из √2116.
Наша задача в том, чтобы определить между какими десятками стоит число 2116.
102 = 100
202 = 400
302 = 900
402 = 1600
502 = 2500
Мы видим что, 2116 больше 1600, но меньше 2500.
Это значит, что число 2116 находится между 402и 502.
41, 42, 43, 44, 45, 46, 47, 48, 49.
Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.
Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.
Как пользоваться таблицей
12 = 1
22 = 4
32 = 9
42 = 16 ⇒ 6
52 = 25 ⇒ 5
62 = 36 ⇒ 6
72 = 49 ⇒ 9
82 = 64 ⇒ 4
92 = 81 ⇒ 1
Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.
Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.
Число 43, возведенное в квадрат, даст число, на конце которого — 9.
Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.
Таким образом, у нас остаются два варианта: 442 и 462.
Далее вычисляем: 44 * 44 = 1936.
46 * 46 = 2116.
Ответ: √2116 = 46
Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.
Еще пример. Извлечем корень из числа √11664
Разложим число 11664 на множители:
11666 : 4 = 2916
2916 : 4 = 729
729 : 3 = 243
243 : 3 = 81
| 11664 | 4 |
| 2916 | 4 |
| 729 | 3 |
| 243 | 3 |
| 81 | 81 |
Запишем выражение в следующем виде:
Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.
Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
- Вычислите значение квадратного корня: √36
- Вычислите значение квадратного корня: √64*36
- Вычислите значение квадратного корня:
- Вычислите значение квадратного корня:
- Вычислите значение квадратного корня:
- Вычислите значение выражения: 4√16 — 12
- Вычислите значение выражения: 5√9 — 8
- Вычислите значение выражения: 7√25 — 10
- Вычислите значение квадратного корня:
- Вычислите значение квадратного уравнения:
- Вычислите значение квадратного уравнения:
- Извлеките квадратный корень из числа √7056 удобным вам способом
Как решаем:7056 4 1764 4 441 3 147 3 49 7 7 7 1 - Вычислите значение квадратного корня √0,81
Ответ: √0,81 = 0,9 - Вычислите значение квадратного корня:
Как решаем:
= 0,09 - Вычислите значение выражения: 8√81 — 20
Как решаем: 8√81 — 20 = 8 * 9 — 20 = 72 — 20 = 52
Ответ: 8√81 — 20 = 52. - Вычислите значение выражения: 13√100 — 15
Как решаем: 13√100 — 15 = 13 * 10 — 15 = 130 — 15 = 115
Ответ: 13√100 — 15 = 115. - Вычислите значение выражения: √16 + 5√4
Как решаем: √16 + 5√4 = 4 + 5 * 4 = 4 + 20 = 24 Ответ: √16 + 5√4 = 24. - Вычислите значение выражения: √36 + 2√9
Как решаем: √36 + 2√9 = 6 + 2 * 3 = 6 + 6 = 12
Ответ: √36 + 2√9 = 12. - Вычислите значение выражения: 2√16 — 3√25
Как решаем: 2√16 — 3√25 = 2 * 4 — 3 * 5 = 8 — 15 = -7
Ответ: 2√16 — 3√25 = -7. - Вычислите значение выражения: 3√81 — 5√9
Как решаем: 3√81 — 5√9 = 3*9 — 5 * 3 = 27 — 15 = 12
Ответ: 3√81 — 5√9 = 12. - Вынесите множитель из-под знака корень: √60
Как решаем: √60 = √15 * √4 = 2√15
Ответ: √60 = 2√15. - Вынесите множитель из-под знака корень: √160
Как решаем: √160 = √16 * √10 = 4√10
Ответ: √160 = 4√10. - Внесите множитель под знак корня: 6√7
Как решаем: √62 * 7 = √36 * √7 = √252
Ответ: 6√7 = √252. - Внесите множитель под знак корня: 8√2
Как решаем: 8√2 = √82 * 2 = √64 * √2 = √128 Ответ: 8√2 = √128. - Внесите множитель под знак корня: 9√5
Как решаем: 9√5 = √92 * 5 = √81 * √5 = √405
Ответ: 9√5 = √405. - Упростите выражение: (5 — √2)2
Как решаем: (5 — √2)2 = 52 — 2 * 5 * √2 + (√2)2 = 25 — 10√2 + 2 = 27 — 10√2.
Ответ: (5 — √2)2 = 27 — 10√2. - Вычислите значение выражения: 3√49 — 3√25
Как решаем: 3√49 — 3√25 = 3 * 7 — 3 * 5 = 21 — 15 = 6
Ответ: 3√49 — 3√25 = 6. - Вычислите значение квадратного корня: √484 * √576
Как решаем: √484 * √576 = 22 * 24 = 528
Ответ: √484 * √576 = 528. - Вычислите значение квадратного корня: √625 * √81
Как решаем: √625 * √81 = 25 * 9 = 225
Ответ: √625 * √81 = 225. - Найдите значение выражения: 3√100 — √144
Как решаем: 3100 — 144 = 3 * 10 — 12 = 18
Ответ: 3√100 — √144 = 18.
Математика: действия со скобками различных видов
Скобки — парные (за небольшим исключением) знаки. Первая называется открывающей, вторая — закрывающей. Они отграничивают определенную часть математического выражения, помогая определиться с порядком выполнения действий.
При решении математических задач применяют 3 разновидности скобок: (), {}, []. Используют, но несколько реже, обратные скобки, которые выглядят так:] и [, а также < и > (уголки). Применение этих знаков всегда является парным, то есть математическое выражение включает открывающуюся и закрывающуюся скобки. Только в этом случае выражение имеет смысл. Назначение этих знаков — разграничение действий и определение последовательности их выполнения.
Область применения круглых скобок:
- обозначение выражений, с которыми выполняются те или иные математические действия. Пример — возведение многочлена в степень: \ и т. д.;
- указание координат точек в одно- и многомерных системах;
- компактная запись периодических десятичных дробей;
- запись отрицательного числа в математическом выражении с целью разделения знаков математического действия и самого числа.
Круглые скобки помогают определиться с последовательностью и приоритетом логических операций и математических действий (как вариант, для изменения существующего алгоритма).
Квадратные знаки применяют для:
- указания целой части числа;
- взятия модуля числа;
- определения порядка действий, аналогично круглым;
- операций с векторами;
- указания скобок второго уровня;
- записи координат, массивов чисел.
Помимо математики, квадратные скобки применяют при записи физических, химических формул, в программировании.
Фигурные скобки ({) используют при обозначении множеств, для объединения уравнений или неравенств в систему, как скобки третьего уровня. Их также применяют при решении систем уравнений (пересечение множеств), а квадратные — [используют для записи их объединения (так называемые совокупности). Рассмотрим примеры с этими символами более подробно.
Нахождение целого по известным процентам
В аквариуме $5$ золотых рыбок, что составляет $25\%$ от общего числа рыбок в аквариуме. Сколько всего рыбок в аквариуме?
Общее число рыбок – это $100\%$. Чтобы найти их, нужно сначала найти $1\%$.
$1\%$ – это не одна рыбка. Это сколько-то рыбок, составляющих сотую долю всех рыбок в аквариуме. Чтобы найти, сколько рыбок составляет эту долю, нужно разделить $5$ на $25$, получится $0.2$
Здесь легко совершить ошибку.
Показать возможную ошибку
Скрыть
Ведь удобнее (и логичнее!) было бы разделить $25$ на $5$. В этом случае у нас получится целое число, $5$ рыбок. Почему же мы делим меньшее на большее?
Предположим, что нам действительно нужно было делить проценты на число, которое их составляет. Тогда один процент – это $5$ рыбок, а $100\%$ – это $500$ рыбок. Но ведь тогда получится, что $25$ процентов – это $25 \cdot 5 = 125$ рыбок! А у нас в задаче сказано, что $25\%$ – это всего лишь $5$.
Следовательно, всё-таки нужно было делить $5$ на $25$. Не беспокойтесь, что в результате получатся «кусочки» рыбок. Это просто какое-то количество от общего числа.
Чтобы узнать, чему равны $100\%$, умножим полученное число на $100$. У нас получится $20$. Это и будет общее число рыбок.
Равенство дробей.
Данная тема достаточно важна на основных свойствах дробей основана вся дальнейшая математика и алгебра
Рассмотренные свойства дробей, не смотря на свою важность очень просты
Чтобы понять основные свойства дробей рассмотрим окружность.
На окружности видно, что 4 части или доли закрашены из восьми возможных. Запишем полученную дробь \(\frac{4}{8}\)
На следующей окружности видно, что закрашена одна часть из двух возможных. Запишем получившеюся дробь \(\frac{1}{2}\)
Если внимательно приглядимся, то увидим, что в первом случае, что во втором случае у нас закрашено половина круга, поэтому полученные дроби равны \(\frac{4}{8} = \frac{1}{2}\), то есть это одно и тоже число.
Как же это доказать математически? Очень просто, вспомним таблицу умножения и распишем первую дробь на множители.
Что мы сделали? Расписали числитель и знаменатель на множители \(\frac{1 \cdot \color{red} {4}}{2 \cdot \color{red} {4}}\), а потом разделили дроби \(\frac{1}{2} \cdot \color{red} {\frac{4}{4}}\). Четыре поделить на четыре это 1, а единица умноженное на любое число это и есть само число. То что мы проделали в приведенном примере называется сокращением дробей.
Посмотрим еще один пример и сократим дробь.
Мы опять расписали числитель и знаменатель на множители и одинаковый числа в числители и знаменатели сократили. То есть два деленное на два дало единицу, а единица умноженная на любое число дает тоже самое число.






























