Точка и прямая на плоскости • образавр

Как применять знание о принадлежности точек к прямой в задачах геометрии и физики

В геометрии:

Определение расстояния от точки до прямой;
Построение точки на прямой;
Вычисление координат точки пересечения двух прямых;
Решение задач на нахождение углов между прямыми или прямой и плоскостью;
Поиск прямой, проходящей через заданную точку и параллельной или перпендикулярной заданной прямой.

В физике:

Решение задач на движение тел по прямой, например, движение автомобиля по прямой дороге;
Определение угла падения света на поверхность и расчет угла отражения;
Поиск траектории движения частицы в электромагнитном поле;
Вычисление векторного произведения двух векторов;
Решение задач на статику, включающих силы, приложенные к объекту на прямой.

Использование знаний о принадлежности точек к прямой позволяет эффективно решать задачи в различных областях науки и техники.

Пример решения задачи
Условие задачи
Решение

Найти расстояние между точкой А(4, 1) и прямой, проходящей через точки В(2, 3) и С(6, 7).
1. Найдем уравнение прямой, проходящей через точки В и С. Для этого узнаем коэффициенты k и b уравнения y=kx+b.

Для этого используем формулу k = (y2-y1)/(x2-x1) и подставляем координаты точек В и С. Получаем k=1.

Для того, чтобы найти b, подставляем координаты одной из точек (например, В) и найденное значение k:

b=y-kx=3-1*2=1.

2. Теперь, имея уравнение прямой, можно найти расстояние до нее от точки А.

Это делается с помощью формулы: d=|kx0-y0+b|/√(k^2+1), где x0 и y0 – координаты точки А.

Подставляем известные значения и получаем:

d=|1*4-1+1|/√(1^2+1)=3/√2.

Ответ: d=3/√2.

Геометрия: определение понятия «принадлежит»

В геометрии понятие «принадлежит» используется для определения связи между объектами в пространстве. Оно помогает нам определить, находится ли один объект внутри или на границе другого объекта.

Чтобы сказать, что точка принадлежит фигуре, нужно убедиться, что эта точка находится внутри фигуры или лежит на ее границе. Это понятие можно использовать для определения отношения точки к линии, полигону, окружности или другим геометрическим фигурам.

Например, в случае окружности, точка считается принадлежащей ей, если она находится внутри окружности или лежит на ее границе. Если точка находится вне окружности, то она не принадлежит ей.

В геометрии возможно также определение принадлежности одной фигуры другой. Например, говоря о треугольнике, можно сказать, что один треугольник принадлежит другому, если все его вершины лежат внутри второго треугольника или на его границе. Если хотя бы одна вершина находится вне второго треугольника, то первый треугольник не принадлежит ему.

Для определения принадлежности используется набор математических формул, соответствующих типу фигуры. Эти формулы основываются на различных свойствах геометрических объектов и позволяют точно определить, принадлежит ли объект другому объекту или нет.

Важно отметить, что принадлежность — относительное понятие и зависит от выбранной системы координат и точки отсчета. Также стоит учесть, что в реальном мире все объекты имеют конечные размеры и не могут быть точками или линиями

Однако, в идеализированной геометрии, мы можем рассматривать объекты в виде идеальных точек, линий или плоскостей для упрощения математических вычислений.

Применение в геометрии

Понимание того, где находится точка относительно прямой, имеет важное значение в геометрии. В геометрических расчетах и построениях мы сталкиваемся с задачами определения положения точки относительно прямой, а также нахождения расстояния от точки до этой прямой

Знание такого положения может помочь нам в решении различных задач, в том числе в построении треугольников или нахождении пересечений в геометрических фигурах.

Для определения положения точки относительно прямой используется понятие «направляющего вектора». Направляющий вектор прямой показывает, в каком направлении расположена прямая и позволяет нам определить, с какой стороны прямой находится данная точка.

Если для определения положения точки мы используем направляющий вектор, то для нахождения расстояния между точкой и прямой применяется формула, основанная на проекции вектора на прямую. Это позволяет нам найти кратчайшее расстояние между точкой и прямой.

Таким образом, понимание положения точки относительно прямой является важным инструментом в геометрии и позволяет нам решать различные задачи, связанные с построением и анализом геометрических фигур.

Определение взаимного расположения двух прямых на плоскости

Для определения взаимного расположения двух прямых на плоскости необходимо учитывать их угловые коэффициенты и значения свободных членов.

Если угловые коэффициенты прямых равны, то они параллельны. В этом случае прямые могут не пересекаться.

Если угловые коэффициенты прямых не равны, тогда они имеют точку пересечения. В этом случае прямые пересекаются в единственной точке на плоскости.

Если угловые коэффициенты прямых равны и значения свободных членов также равны, то прямые совпадают. В этом случае все точки прямых являются точками пересечения.

Определение взаимного расположения двух прямых на плоскости основано на рассмотрении их уравнений в общем виде. Принципы, позволяющие определить их взаимное положение, могут быть использованы для решения геометрических задач или анализа систем уравнений с прямыми.

Окрестность и прямая линия

Процесс доказательства состоит из следующих шагов:

Выберите одну из трех точек и обозначьте ее как точку «A».
Постройте окружность с центром в точке «A» и проходящую через две остальные точки. Определите радиус этой окружности и обозначьте его как «r».
Отметьте центры окружностей, которые можно построить с помощью других двух точек из исходного набора.

Использование окрестности и построение окружностей позволяют наглядно представить взаимное расположение точек на плоскости и убедиться в их линейной вытянутости. Этот метод доказательства может быть использован в различных задачах геометрии и математики, где требуется доказать линейное положение точек.

Практическое значение

В науке и инженерии, определение принадлежности точек прямой может быть полезным при решении задач геометрии, например, при проектировании зданий, создании машин и приборов, анализе пространственных данных и моделировании сложных систем.

В технических специальностях, таких как авиация, аэрокосмическая индустрия, автомобильный и судостроительный секторы, знание методов определения принадлежности точек прямой помогает инженерам осуществлять точное позиционирование и измерение объектов.

В информационных технологиях и программировании методы определения принадлежности точек прямой используются для создания алгоритмов и программ, которые могут обрабатывать и анализировать большие объемы данных, решать задачи компьютерного зрения и обработки изображений, а также определять расположение и движение объектов в пространстве.

В анализе данных и статистике, определение принадлежности точек прямой может быть полезным при построении и визуализации графиков, проведении регрессионного анализа, моделировании и прогнозировании данных, а также при изучении связей и зависимостей между переменными.

Кроме того, знание методов определения принадлежности точек прямой может быть полезным в повседневной жизни, например, при планировании маршрутов, определении местоположения на карте или при оценке расстояний и времени в путешествиях или спорте.

Инструкция

Проверить принадлежность точки
той либо иной прямой
довольно просто. Используйте для этого уравнение прямой
. Итак, предположим, что прямая проходит через точки
А(x1,y1) и В(x2,y2). Дана точка К(x,y): нужно проверить ее принадлежность прямой
. Уравнение линии по двум точкам имеет следующий вид: (x — x1) * (y2 — y1) — (x2 — x1) * (y — y1) = 0.

Подставьте значение координат точки
К в уравнение. Если (x — x1) * (y2 — y1) — (x2 — x1) * (y — y1) окажется больше нуля, то точка К расположена правее или ниже прямой
, проведенной по точкам А и В.

В том случае, если (x — x1) * (y2 — y1) — (x2 — x1) * (y — y1) будет меньше нуля, точка К располагается выше или левее линии. Другими словами, только в том случае, если уравнение вида (x — x1) * (y2 — y1) — (x2 — x1) * (y — y1) = 0 справедливо, точки
А, В и К будут расположены на одной прямой
.

Если точки А, B и С лежат на одной прямой, то больший из отрезков AB, ВС и АС равен сумме двух других. По условию больший из данных отрезков (отрезок АС) равен 5 см, а сумма двух других (AB+BC) равна 7 см. Поэтому точки А, B и С не лежат на одной прямой.

Если точки А, В, С лежат на одной прямой, то больший из отрезков АВ, ВС и АС равен сумме двух других. По условию больший из данных отрезков (АС =5 см), а АВ + ВС = 7 см, поэтому точки А, В, С не лежат на одной прямой.

Похожие задачи:

1. Площадь ромба равна S. Найдите площадь четырехугольника, вершинами которого являются середины сторон ромба.

2. Две окружности с центрами в точках О1 и О2 пересекаются в точках А и А1, а отрезки АВ и АС — их диаметры. Найдите величины углов АА1В и АА1С и докажите, что точки В, А1 и С лежат на одной прямой.

3. Медианы треугольника со сторонами 5 см, 6 см и 7 см пересекаются в точке О. Найдите расстояние от точки О до прямых, содержащих стороны треугольника.

4. Четырехугольник ABCD вписан в окружность. Известно, что угол ABD=30*, угол ACB=30*, угол BDC=20*. Найти углы четырехугольника ABCD.

1) Катеты прямоугольного треугольника равны 15см и 20см. Найдите длину окружности, диаметром которой является высота, проведенная к гипотенузе.

2) Площадь квадрата равна S. Найдите:

а) длину вписанной окружности

б) длину дуги, заключенной между двумя соседними точками касания.

в) площадь части квадрата, лежащей вне вписанной окружности.

1. Две окружности с центрами О и К имеют соответственно радиусы 4 и 8 см. Найдите радиусы окружностей, касающихся одновременно двух данных, если их центры лежат на прямой ОК, и отрезок ОК равен 6 см.

2. Высоты треугольника, пересекаясь в точке Н, образуют шесть углов с вершиной в точке Н. Определите эти углы, если углы данного треугольника равны: 50, 60, 70 градусов.

Что входит в состав KMS Tools

Как уже упоминалось выше, KMS Tools состоит из нескольких утилит. Каждая из них имеет различный функционал и возможности, а также совместимость с конкретными операционными системами и архитектурами.

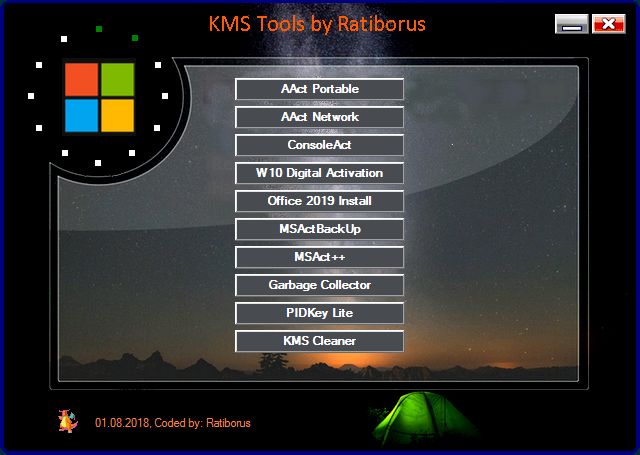
Чтобы успешно провести активацию нужного вам софта и ОС важно знать, за что отвечает каждая программа:

AAct – софт для активации Windows и Office при помощи KMS-сервера.
AAct Network – тот же функционал, что и в предыдущей программе, однако она разработана для активации сразу нескольких компьютеров в локальной сети.
Garbage Collector – софт для поиска и удаления мусора и ненужных файлов, связанных с активацией Windows и Office.
KMSAuto Lite – софт для активации Windows и Office при помощи KMS-сервера при помощи встроенного и внутреннего KMS-сервера.
KMSAuto Net – аналогичный предыдущему софт, но с несколько большим функционалом.
KMSCleaner – сервис для очистки системы от следов предыдущих активаций.
MSActBackUp – софт для резервного копирования и восстановления активации продуктов Microsoft.
MSAct++ — софт для активации Windows и Office с использованием KMS и MAK ключей.
Office 2013-2019 C2R Install – активация и получение лицензии офисных пакетов сборок от 2013 по 2019.
PIDKey Lite – утилита для проверки и сохранения ключей продуктов Microsoft.

Точки и прямая

Точки – это основные объекты геометрии. Точка – это место на плоскости, которое не имеет длины, ширины и высоты. Точки могут быть расположены как на прямой, так и вне ее.

Лежание точки на прямой – одно из фундаментальных понятий геометрии. Точка может находиться на прямой, вне прямой или даже являться самой прямой. Если точка находится на прямой, то говорят, что она «лежит на прямой».

Лежат ли точки по одну сторону от прямой – это вопрос, который часто встречается в геометрии. Для решения этого вопроса нужно построить параллельную прямую, которая проходит через данную точку, и проверить, находятся ли остальные точки по одну сторону от этой прямой.

Например: Если точка находится выше прямой, то все остальные точки должны находиться выше этой прямой. Если точка находится ниже прямой, то все остальные точки должны находиться ниже этой прямой.

Понимание лежания точек по одну сторону от прямой имеет большое значение в геометрии и может применяться для решения различных задач.

Как определяется «принадлежность» в геометрии?

В геометрии термин «принадлежность» относится к определению, находится ли точка, прямая, плоскость или другая геометрическая фигура внутри или на границе другого объекта геометрии. Определение «принадлежности» в геометрии может быть разным для различных типов фигур.

Например, для точки принадлежность может быть определена путем проверки, лежит ли она внутри или на границе заданной фигуры. Для прямых и плоскостей принадлежность может быть определена путем проверки, пересекают ли они другие фигуры.

Способы определения «принадлежности» могут включать использование математических формул, уравнений или алгоритмов. Например, для прямых и плоскостей могут использоваться уравнения, в которых проверяется, соответствуют ли координаты точки условиям уравнения. Если точка соответствует условиям уравнения, то она принадлежит прямой или плоскости, иначе она не принадлежит.

В некоторых случаях «принадлежность» может также определяться с помощью геометрических свойств фигур. Например, если точка лежит внутри окружности, то она принадлежит окружности. Если точка лежит внутри треугольника, то она принадлежит треугольнику.

В геометрии важно точно определить «принадлежность», чтобы правильно решать задачи и проводить доказательства. Точное определение «принадлежности» помогает установить отношения между различными объектами геометрии и использовать их свойства для решения задач

Что такое прямая?

Прямую можно определить как путь, который можно пройти между двумя точками самым кратчайшим способом. Каждая точка на прямой имеет свои координаты, которые можно представить в виде пары чисел (x, y) или в виде уравнения прямой: y = mx + b. Где m — это коэффициент наклона прямой, а b — точка пересечения с осью y.

Прямой присущи несколько основных свойств:

На прямой любые две точки всегда можно соединить отрезком, который будет находиться полностью на прямой.
Прямая делит плоскость на две полуплоскости.
Прямая в любом месте может быть перпендикулярна к другой прямой, что означает, что угол между этими прямыми равен 90 градусов.

Первоначально прямая была представлена как основной элемент геометрии, и она используется в различных областях, включая математику, физику, инженерию и компьютерную графику.

Ошибки активации

Порой у пользователей во время активации могут возникнуть проблемы и вылетать ошибки. В случае в работе с KMS Tools причин, почему появляются ошибки – крайне мало и что самое главное – они быстро и просто решаются.

Основные причины ошибок и их решения:

Несовместимость KMS Tools и версии Windows\Office – выбирайте утилиту, которая точно активирует конкретную сборку ОС или софта.
Работе активатора мешает антивирус и Защитник Windows – в таком случае нужно отключить на время антивирус и сам активатора добавить в исключения, а также отключить Защитник Windows (подействует после перезагрузки ПК) и только потом начинать работать с KMS Tools.
Используется не актуальная версия KMS Tools – Windows и Office регулярно получают обновления, а потому юзеры обязаны также всегда использовать актуальный активатор.

Определение системы координат

В двумерной системе координат используются две взаимно перпендикулярные оси — горизонтальная (ось абсцисс) и вертикальная (ось ординат). Точка на плоскости определяется двумя координатами — абсциссой и ординатой. В результате получается пара чисел (x, y), где x — абсцисса точки по горизонтальной оси, а y — ордината точки по вертикальной оси.

В трехмерной системе координат добавляется третья ось — ось аппликат. Точка в пространстве определяется тремя координатами — абсциссой, ординатой и аппликатом. В результате получается тройка чисел (x, y, z), где x — абсцисса точки по горизонтальной оси, y — ордината точки по вертикальной оси, а z — аппликата точки по третьей оси.

Система координат	Оси	Единицы измерения
Двумерная	Горизонтальная (ось абсцисс), Вертикальная (ось ординат)	Единицы длины
Трехмерная	Горизонтальная (ось абсцисс), Вертикальная (ось ординат), Ось аппликат	Единицы длины

Метод расчета площадей треугольников

1. Полупериметр и радиус вписанной окружности

Если известны стороны треугольника и радиус вписанной окружности, площадь можно вычислить по следующей формуле:

Находим полупериметр треугольника по формуле: p = (a + b + c) / 2.
Вычисляем площадь треугольника по формуле: S = p * (p-a) * (p-b) * (p-c), где a, b и c — длины сторон треугольника.

2. Координаты вершин треугольника

Если известны координаты вершин треугольника, площадь можно вычислить по формуле Гаусса:

Вычисляем площадь треугольника по формуле: S = 0.5 * |(x1 * (y2 — y3) + x2 * (y3 — y1) + x3 * (y1 — y2))|, где (x1, y1), (x2, y2) и (x3, y3) — координаты вершин треугольника.

3. Высота и основание

Если известны высота треугольника и длина его основания, площадь можно вычислить по формуле:

Находим площадь треугольника по формуле: S = (h * b) / 2, где h — высота треугольника, b — длина основания.

Зная хотя бы одну из указанных величин, можно точно вычислить площадь треугольника.

Методы доказательства

Существует несколько методов, позволяющих доказать, что точка принадлежит прямой:

1. Геометрический метод

Геометрический метод доказательства основан на использовании свойств и определений геометрии. Для того чтобы доказать, что точка принадлежит прямой, можно воспользоваться следующими свойствами:

теоремой о средней линии;
теоремой о линейной комбинации;
теоремой о пересечении прямых и много другими.

Используя эти свойства и определения, можно провести необходимые линии и углы, и таким образом доказать, что точка принадлежит прямой.

2. Алгебраический метод

Алгебраический метод доказательства основан на использовании алгебраических операций и равенств. Для того чтобы доказать, что точка принадлежит прямой, можно воспользоваться следующими методами:

записать уравнение прямой и подставить координаты точки в это уравнение;
построить уравнение прямой, проходящей через две известные точки, и проверить, удовлетворяет ли координаты данной точки этому уравнению;
воспользоваться системами уравнений и много другими.

Используя эти методы, можно получить уравнение, которое выполняется для данной точки, и таким образом доказать, что точка принадлежит прямой.

3. Комбинированный метод

Комбинированный метод доказательства основан на использовании и геометрических, и алгебраических методов. Для того чтобы доказать, что точка принадлежит прямой, можно воспользоваться сочетанием геометрических свойств и алгебраических выкладок:

выразить координаты точки через параметры заданной прямой и проверить, выполняются ли эти равенства;
воспользоваться геометрическими построениями, чтобы проверить, что данная точка принадлежит прямой;
рассмотреть особые случаи и много другими.

Используя этот метод, можно объединить различные подходы и доказать принадлежность точки прямой.

Графический метод

Для проведения графического метода необходимо знать уравнение прямой, а также координаты точки, которую нужно проверить.

Для построения графика прямой необходимо:

Найти две различные точки, принадлежащие прямой. Для этого можно приравнять одну из координат к нулю и найти значение второй координаты.
Провести прямую, соединяющую найденные точки. Эта прямая будет графиком уравнения прямой.

После построения графика прямой можно определить, принадлежит ли данная точка прямой. Для этого необходимо проверить, лежит ли данная точка на построенном графике. Если точка лежит на графике, то она принадлежит прямой.

Графический метод является достаточно простым и понятным способом доказательства принадлежности точки прямой, однако он может быть неприменим в определенных случаях, например, если график прямой не удается построить с высокой точностью или если прямая задана неявно.

Аналитический метод

Аналитический метод позволяет доказать, что точка принадлежит прямой с использованием алгебраических выкладок и уравнений, описывающих прямую и точку.

Для начала, вспомним уравнение прямой в общем виде: ax + by + c = 0, где a и b — это коэффициенты, описывающие наклон прямой, а c — свободный член.

Итак, чтобы доказать, что точка принадлежит прямой, необходимо подставить координаты точки (x, y) в уравнение прямой и проверить, выполняется ли равенство.

Приведем пример. Пусть у нас есть точка с координатами (2, 3) и прямая с уравнением 2x — 3y + 5 = 0. Чтобы проверить, принадлежит ли данная точка прямой, подставим ее координаты в уравнение:

2 * 2 — 3 * 3 + 5

= 4 — 9 + 5

= 0

Результат равен нулю. Это означает, что точка (2, 3) принадлежит прямой, так как равенство выполняется.

Таким образом, аналитический метод позволяет четко и логически доказать, что точка принадлежит прямой, основываясь на алгебраических выкладках и уравнениях прямой и точки.