Знакомство с матрицами

Важность модуля матрицы

Важность модуля матрицы заключается в том, что он позволяет измерить величину изменений, происходящих с этой матрицей. Например, при решении системы линейных уравнений, модуль матрицы может указывать на наличие или отсутствие решений, а также на их единственность или множественность

Кроме того, модуль матрицы может использоваться для определения некоторых важных характеристик матрицы, таких как ранг или определитель. Например, модуль определителя матрицы может показывать, является ли эта матрица вырожденной или невырожденной.

Также модуль матрицы может быть связан с определенными свойствами системы векторов или уравнений. Например, модуль определенной части матрицы может помочь определить, является ли эта часть базисом или линейно зависимой системы векторов.

Таким образом, понимание и использование модуля матрицы является важным элементом математического анализа и решения различных задач, связанных с линейной алгеброй и теорией матриц.

Модуль матрицы: как его вычислить

Модуль матрицы – это число, полученное вычислением суммы всех элементов матрицы с неотрицательными знаками. Вычисление модуля матрицы может быть полезным во многих задачах, таких как выявление ранга матрицы или решение линейных уравнений.

Для вычисления модуля матрицы необходимо пройти по каждому элементу матрицы и посчитать сумму всех неотрицательных значений. Например, для матрицы 3×3:

-2	6	8
2	-4	3
5	10	1

Модуль матрицы вычисляется так:

1. Найти сумму всех неотрицательных элементов матрицы:

6 + 8 + 2 + 3 + 5 + 10 + 1 = 35

Найти сумму всех отрицательных элементов матрицы:

-2 — 4 = -6

Найти модуль матрицы:

|М| = 35 — (-6) = 41

Таким образом, модуль матрицы для данной матрицы 3×3 равен 41.

Практическое применение модуля матрицы

Модуль матрицы — это важный инструмент в линейной алгебре и находит широкое применение в различных областях науки и техники. Рассмотрим несколько практических примеров его использования.

Криптография

Модуль матрицы широко используется в криптографии, например, для зашифрования сообщений. Для этого используют матрицы ключей, которые подвергаются специальным преобразованиям с помощью модуля матрицы.

Искусственный интеллект

В области искусственного интеллекта модуль матрицы применяется для решения задач машинного обучения. В частности, матричные вычисления используются для обучения нейронных сетей, распознавания образов и прогнозирования данных.

Компьютерная графика

В компьютерной графике модуль матрицы используется для выполнения преобразований над объектами, например, для их перемещения, поворота или масштабирования. Это позволяет создавать реалистичные 3D модели и анимации.

Механика

Модуль матрицы используется в механике для анализа и решения задач, связанных с движением твердых тел. Например, матрицы преобразования используются для описания движения объектов в пространстве.

Статистика и эконометрика

В статистике и эконометрике модуль матрицы используется для решения задач линейной регрессии, а также для анализа данных и прогнозирования тенденций.

Таким образом, модуль матрицы имеет множество практических применений в различных областях науки и техники. Он позволяет выполнять сложные вычисления и анализировать данные, что делает его важным инструментом для исследования и разработки новых технологий.

Определение модуля матрицы и его свойства

Модуль матрицы – это число, равное определителю ее элементов. Он обозначается как |A|, где A – матрица.

Модуль матрицы имеет несколько свойств, которые упрощают его вычисление:

• Модуль транспонированной матрицы равен модулю исходной матрицы, то есть |A^T| = |A|;
• Модуль противоположной матрицы также равен модулю исходной матрицы, то есть |-A| = |A|;
• Модуль произведения матриц равен произведению их модулей, то есть |AB| = |A| * |B|.

Также модуль матрицы можно вычислить с помощью приведения ее к треугольному виду, где на диагонали стоят ее главные элементы. Модуль матрицы в таком виде равен произведению главных элементов, то есть |A| = a₁₁ * a₂₂ * … * a_nn, где a_ij – элемент матрицы на пересечении i-й строки и j-го столбца.

Модуль матрицы находит широкое применение в линейной алгебре, в задачах оптимизации и теории кодирования.

Собираем трансформации вместе

Итак, теперь мы умеем поворачивать, переносить и масштабировать наши векторы. Следующий шагом было бы неплохо объединить трансформации, что реализуется по следующей формуле:

ВНИМАНИЕ! Эта формула на самом деле показывает, что сначала выполняется масштабирование, потом поворот и только в самую последнюю очередь выполняется перенос. Именно так работает перемножение матриц

Обязательно запомните в каком порядке все это выполняется, потому что порядок действительно важен, в конце концов вы можете сами это проверить:

• Сделайте шаг вперед и повернитесь влево
• Повернитесь влево и сделайте шаг вперед

Разницу действительно важно понимать, так как вы постоянно будете с этим сталкиваться. К примеру, когда вы будете работать с игровыми персонажами или какими-то объектами, то всегда сначала выполняйте масштабирование, потом поворот и только потом перенос

На самом деле, приведенный выше порядок — это то, что вам обычно нужно для игровых персонажей и других предметов: сначала масштабируйте его, если это необходимо; затем установливаете его направление, а затем перемещаете его. Например, для модели судна (повороты удалены для упрощения):

• Неправильный путь :
  • Вы переносите корабль на (10, 0, 0). Его центр теперь находится в 10 единицах от начала координат.
  • Вы масштабируете свой корабль в 2 раза. Каждая координата умножается на 2 “относительно исходной”, что далеко… Итак, вы попадаете в большой корабль, но его центр 2 * 10 = 20. Не то, что вы хотели.
• Правильный путь :
  • Вы масштабируете свой корабль в 2 раза. Вы получаете большой корабль, с центром в начале координат.
  • Вы переносите свой корабль. Он по прежнему того же размера и на правильном расстоянии.

В C++, с GLM :

В GLSL :

Мировая, видовая и проекционная матрицы

До конца этого урока мы будем полагать, что знаем как отображать любимую 3D модель из Blender — обезьянку Suzanne.

Мировая, видовая и проекционная матрицы — это удобный инструмент для разделения трансформаций.

Матрицы. Действия с матрицами

Матрицей размерности m x n называется прямоугольная таблица m x n чисел a ij , i=1,…, m, j=1,…, n:

расположенных в m строках и n столбцах. Матрица называется квадратной, если m=n (n — порядок матрицы). 

Линейные матричные операции

По определению, чтобы умножить матрицу на число, нужно умножить на это число все элементы матрицы. 

Суммой двух матриц одинаковой размерности, называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых. 

Произведение матриц определяется следующим образом. Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если 

, ,

то произведением матриц A и B, называется матрица 

,

элементы которой вычисляются по формуле 

c ij =a i1 b 1j + a i2 b 2j + … +a in b nj , i=1, …, m, j=1, …, k.

Произведение матриц A и B обозначается AB, т.е. C=AB. 

Произведение матриц, вообще говоря, зависит от порядка сомножителей. Если AB=BA, то матрицы A и B называются перестановочными. 

Для квадратных матриц определена единичная матрица — квадратная матрица, все диагональные элементы которой единицы, а остальные — нули: 

Единичная матрица чаще всего обозначается буквой E или E n, где n — порядок матрицы. Непосредственным вычислением легко проверить основное свойство единичной матрицы:

AE=EA=A.

Скалярной матрицей называется диагональная матрица с одинаковыми числами на главной диагонали; единичная матрица — частный случай скалярной матрицы. 

Для квадратных матриц определена операция возведения в целую неотрицательную степень:

A 0 =E, A 1 =A, A 2 =AA, …, A n =A n-1 A, ….

Для прямоугольных матриц определена операция транспонирования. Рассмотрим произвольную прямоугольную матрицу A. Матрица, получающаяся из матрицы A заменой строк столбцами, называется транспонированной по отношению к матрице и обозначается A T:

, .

Верны соотношения:

(AT )T =A;

(A+B)T=AT +BT ;

(AB)T =BT AT.

Квадратная матрица A, для которой A T =A, называется симметричной. Элементы такой матрицы, расположенные симметрично относительно главной диагонали, равны. 

Квадратная матрица A называется обратимой, если существует такая матрица X, что

AX=XA=E. 

Матрица X называется обратной к матрице A и обозначается A -1, т.е. 

A A -1 =A -1A=E. 

Известно, что если матрица A невырождена (т.е ее определитель отличен от нуля), то у нее существует обратная матрица A -1.

Верно соотношение: (A-1)T =(AT ) -1.

Квадратная матрица U, для которой U -1 =U T, называется ортогональной матрицей. 

Свойства ортогональной матрицы:

• Модуль определителя ортогональной матрицы равен единице. 

• Сумма квадратов элементов любого столбца ортогональной матрицы равна единице. 

• Сумма произведений элементов любого столбца ортогональной матрицы на соответствующие элементы другого столбца равна нулю. Такими же свойствами обладают строки ортогональной матрицы.

Как определяется модуль матрицы

Для определения модуля матрицы необходимо выполнить следующие шаги:

1. Взять каждый элемент матрицы по отдельности и возвести его в квадрат.
2. Суммировать все полученные квадраты элементов матрицы.
3. Взять квадратный корень из полученной суммы.

Таким образом, если у нас есть матрица A размерности m x n, где m — количество строк, а n — количество столбцов, то модуль матрицы A обозначается как |A| и вычисляется следующим образом:

|A| = sqrt(a₁₁2 + a₁₂2 + … + a_1n2 + a₂₁2 + a₂₂2 + … + a_mn2)

Здесь a_ij — элемент матрицы, находящийся в i-й строке и j-м столбце.

Таким образом, модуль матрицы является одним из способов определения «величины» данной матрицы, позволяя характеризовать ее общую силу или интенсивность.

Что такое модуль матрицы и зачем он нужен?

Модуль матрицы может быть вычислен путем нахождения суммы модулей ее элементов или путем вычисления определителя матрицы. Определитель матрицы – это число, которое получается из ее элементов с помощью определенных правил. Знание модуля матрицы может быть полезно в различных областях, например, в алгебре, теории вероятностей, физике и др.

Зачем нужно вычислять модуль матрицы? Первое, что можно отметить, это использование модуля матрицы в линейной алгебре для определения поведения системы линейных уравнений. Модуль матрицы позволяет узнать, насколько осилены или слабы системы уравнений и помогает анализировать их свойства.

Кроме того, модуль матрицы может быть полезен в статистике при анализе данных. Например, модуль матрицы может помочь выделить наиболее важные признаки в наборе данных, исключая незначительные или коррелированные с другими признаки. Это может упростить анализ данных и помочь найти закономерности или тренды.

Таким образом, модуль матрицы является важной величиной, которая позволяет изучать и анализировать различные аспекты объектов и явлений в различных областях знания

Работа с матрицей с помощью NumPy

Мы можем выполнять все операции с матрицей, используя numpy.array(), такие как сложение, вычитание, транспонирование, нарезание матрицы и т. д.

Добавление матрицы

Мы создадим две матрицы с помощью функции numpy.array() и добавим их с помощью оператора +. Давайте разберемся в следующем примере.

Пример –

 
import numpy as np 
mat1 = np.array(, , ]) 
mat2 = np.array(, , ]) 
mat3 = mat1 + mat2   
print("The matrix addition is: ") 
print(mat3) 

Выход:

The matrix addition is:  
 
  
 ] 

Умножение

Мы будем использовать метод numpy.dot() для умножения обеих матриц. Это точечное умножение матриц mat1 и mat2, обрабатывает 2D-массив и выполняет умножение.

Пример –

 
import numpy as np 
mat1 = np.array(, ]) 
mat2 =  np.array(, ]) 
mat3 = mat1.dot(mat2)   
print("The matrix is:") 
print(mat3) 

Выход:

The matrix is: 
 
 ] 

Нарезка элементов

Мы можем разрезать элемент матрицы, как в стандартном списке Python. Нарезка возвращает элемент на основе индекса начала / конца. Мы также можем сделать отрицательную нарезку. Синтаксис приведен ниже.

Синтаксис –

 
arr  

Arr представляет имя матрицы. По умолчанию начальный индекс равен 0, например – , это означает, что начальный индекс равен 0. Если мы не предоставим конечное значение, он будет учитывать длину массива. Мы можем передавать отрицательные значения индекса как в начало, так и в конец. В следующем примере мы применим нарезку в обычном массиве, чтобы понять, как она работает.

Пример –

 
import numpy as np 
 
arr = np.array() 
print(arr) # It will print the elements from 2 to 4 
print(arr) # It will print the elements from 0 to 3 
print(arr) # It will print the elements from 3 to length of the array. 

Выход:

Теперь мы реализуем нарезку по матрице. Для выполнения следуйте синтаксису ниже.

Mat1

В приведенном выше синтаксисе:

• Первое начало / конец представляет строки, которые означают выбор строк матрицы.
• Первое начало / конец представляет столбцы, которые означают выбор столбца матрицы.

Мы будем выполнять нарезку в приведенной ниже матрице.

 
mat1 = np.array(, 
    , 
    , 
    ]) 

Вышеупомянутая матрица состоит из четырех строк. В 0-м ряду есть , в 1-й строке – и так далее. В нем пять столбцов. Рассмотрим на примере.

Пример –

 
import numpy as np  
mat1 = np.array(, 
    , 
    , 
    ]) 
print(mat1) 

Выход:

 
 ] 

Объяснение:

В приведенном выше примере мы напечатали первую и вторую строки и нарезали первый, второй и третий столбцы. Согласно синтаксису нарезки мы можем получить любые строки и столбцы.

Пример – печать первой строки и всех столбцов:

 
import numpy as np 
mat1 = np.array(, 
    , 
    , 
    ]) 
print(mat1) 

Выход:

] 

Пример – печать строк матрицы:

 
import numpy as np 
mat1 = np.array(, , ]) 
print(mat1)  #first row 
print(mat1) # the second row 
print(mat1) # -1 will print the last row 

Выход:

Сложение и умножение на число.

Пусть \(A\) и \(B\) — матрицы размеров \(m \times n\). Мы можем сопоставить им третью матрицу \(C\) размеров \(m \times n\), элементы которой \(c_{ij}\) связаны с элементами и матриц \(A\) и \(B\) равенствами
$$
c_{ij}=a_{ij}+b_{ij}\ (i=1, \ldots, m,\ j=1, \ldots, n).\label{ref1}
$$

Определение.

Матрица \(C\), определяемая по \(A\) и \(B\) формулой \eqref{ref1}, называется их суммой и обозначается \(A+B\).

Определение.

Матрица \(C\), элементы которой \(c_{ij}\) равны произведениям элементов \(a_{ij}\) матрицы \(A\) на число \(\alpha\), называется произведением \(A\) на \(\alpha\) и обозначается \(\alpha A\). Мы имеем
$$
c_{ij}=\alpha a_{ij}\ (i=1, \ldots, m,\ j=1, \ldots, n).\label{ref2}
$$

Из свойств сложения и умножения чисел легко вытекает наше первое утверждение.

Утверждение 1.

Для любых матриц \(A, B, C\) и любых чисел \(\alpha\) и \(\beta\) выполнены равенства:

• \(A+B=B+A\),
• \((A+B)+C=A+(B+C)\),
• \(\alpha(A+B)=\alpha A+\alpha B\),
• \((\alpha+\beta)A=\alpha A+\beta A\),
• \((\alpha\beta)A=\alpha(\beta A)\).

Матрица, все элементы которой равны нулю, называется нулевой матрицей. Если \(O\) — нулевая матрица размеров \(m \times n\), то для любой матрицы тех же размеров
$$
A+O=A.\nonumber
$$

Матрицу \((-1)A\) называют противоположной матрице \(A\) и обозначают \(-A\). Она обладает тем свойством, что
$$
A+(-A)=O.\nonumber
$$

Сумма матриц \(B\) и \(-A\) называется разностью матриц \(B\) и \(A\) и обозначается \(B-A\). Мы видим, что сформулированные выше свойства линейных операций с матрицами совпадают со свойствами . Используя линейные операции, мы можем составлять из матриц одинаковых размеров \(A_{1}, \ldots, A_{k}\) и чисел \(\alpha_{1}, \ldots, \alpha_{k}\), выражения вида
$$
\alpha_{1}A_{1}+\ldots+\alpha_{k}A_{k}.\nonumber
$$

Такие выражения называются линейными комбинациями матриц. Если какая-то матрица представлена как линейная комбинация других матриц, то говорят, что она по ним разложена.

Пример 1.

Пусть \(\boldsymbol{p}_{1}, \ldots, \boldsymbol{p}_{k}\), — столбцы одинаковой высоты \(n\). Тогда столбец \(\boldsymbol{q}\) той же высоты по ним разложен, если при некоторых коэффициентах \(\alpha_{1}, \ldots, \alpha_{k}\)
$$
\boldsymbol{q}=\alpha_{1}\boldsymbol{p}_{1}+\ldots+\alpha_{k}\boldsymbol{p}_{k},\nonumber
$$
или, в более подробной записи,
$$
\begin{Vmatrix} q^{1}\\
\vdots\\
q^{n}
\end{Vmatrix}=\alpha_{1}
\begin{Vmatrix} p_{1}^{1}\\
\vdots\\
p_{1}^{n} \end{Vmatrix}+\ldots+\alpha_{k} \begin{Vmatrix} p_{k}^{1}\\
\vdots\\
p_{k}^{n} \end{Vmatrix}.\nonumber
$$
В силу определения линейных операций это матричное равенство равносильно \(n\) числовым равенствам
$$
\begin{matrix}
q^{1}=\alpha_{1}p_{1}^{1}+\ldots+\alpha_{k}p_{k}^{1},\\
\ldots\\
q^{n}=\alpha_{1}p_{1}^{n}+\ldots+\alpha_{k}p_{k}^{n}.
\end{matrix}\nonumber
$$

Вычисление модуля матрицы

Модуль матрицы определяется как сумма элементов матрицы по всем строкам и столбцам.

Для вычисления модуля матрицы необходимо выполнить следующие шаги:

1. Пройти по всем элементам матрицы. Для этого используется двойной цикл, вложенный один в другой. Первый цикл проходит по строкам, а второй цикл — по столбцам.

2. На каждом шаге суммировать значение элемента с общей суммой модуля. Для этого используется переменная, которая будет хранить общую сумму.

3. После завершения циклов получим сумму элементов матрицы. Это и будет модуль матрицы.

Рассмотрим пример:

// Создание матрицы
int[][] matrix = {
{1, 2, 3},
{4, -5, 6},
{-7, 8, 9}
};
// Инициализация переменной для хранения модуля
int moduleSum = 0;
// Вычисление модуля матрицы
for (int i = 0; i 

В результате выполнения данного кода будет выведено значение модуля матрицы.

Формулы для определения модуля матрицы

Модуль матрицы представляет собой числовое значение, выражающее «величину» или «размер» данной матрицы. В зависимости от особенностей матрицы существуют различные способы определения ее модуля.

Если речь идет о квадратной матрице, то модуль матрицы может быть определен как следующая сумма:

mod(A) = |A| = |a11*a22*a33*…*ann|

где a_ij — элементы матрицы, n — размерность матрицы.

Если матрица не является квадратной, то ее модуль может быть определен с помощью формулы:

• mod(A) = |A| = √(a₁₁2 + a₁₂2 + a₁₃2 + … + a_1m2),
• где a_ij — элементы матрицы, m — количество строк, n — количество столбцов.

Также существуют другие способы определения модуля матрицы, которые зависят от конкретных характеристик и свойств матрицы.

Особенности модуля матрицы

Определитель матрицы является важным показателем, который характеризует свойства данной матрицы. Модуль определителя позволяет определить, насколько матрица «растягивает» пространство, образованное ее столбцами или строками.

Особенности модуля матрицы включают следующее:

Свойства модуля матрицы
Описание
Значение отлично от нуля
Если модуль матрицы отличен от нуля, то это означает, что матрица обратима и можно найти ее обратную матрицу.
Значение равно нулю
Если модуль матрицы равен нулю, то это означает, что матрица невырожденная и необратима. В этом случае система линейных уравнений, связанная с данной матрицей, может иметь бесконечное количество решений.
Значение больше нуля
Если модуль матрицы больше нуля, то это означает, что матрица является положительно определенной

Это важное свойство матрицы в линейной алгебре и теории оптимизации.
Значение меньше нуля
Если модуль матрицы меньше нуля, то это означает, что матрица является отрицательно определенной. Это также важное свойство матрицы и может использоваться в различных областях, например, в физике.

Таким образом, модуль матрицы позволяет определить ряд важных свойств и характеристик данной матрицы, которые могут быть полезными в различных областях науки и техники.

Практическое применение модуля матрицы

Одним из основных применений модуля матрицы является решение систем линейных уравнений. При решении системы линейных уравнений с помощью метода Крамера, необходимо вычислить модуль матрицы коэффициентов системы. Если модуль матрицы равен нулю, то система не имеет решений. Если модуль матрицы не равен нулю, то система имеет единственное решение, которое может быть найдено с помощью формул Крамера.

Еще одним применением модуля матрицы является нахождение обратной матрицы. Обратная матрица существует только тогда, когда модуль матрицы не равен нулю. При помощи обратной матрицы можно решать системы линейных уравнений, находить решения линейных дифференциальных уравнений, а также проводить анализ матрицы на сходимость и устойчивость.

Модуль матрицы также применяется в задачах оптимизации. Часто возникает задача минимизации функции, зависящей от нескольких переменных. Модуль матрицы может быть использован для проверки определенных условий оптимальности, например, условий достаточности.

В области машинного обучения модуль матрицы может быть использован для оценки качества модели. Например, в задаче классификации, модуль матрицы может быть использован для измерения разницы между предсказанными значениями и реальными значениями целевой переменной. Чем меньше модуль матрицы, тем ближе предсказания модели к реальным значениям.

Таким образом, модуль матрицы имеет широкое практическое применение и используется в различных областях науки и техники для решения разнообразных задач.

Правильная расстановка индексов в матрице

Матрица — это просто таблица, заполненная числами. Нео тут ни при чём.

Одна из ключевых характеристик матрицы — это её размерность, т.е. количество строк и столбцов, из которых она состоит. Обычно говорят, что некая матрица $A$ имеет размер $\left$, если в ней имеется $m$ строк и $n$ столбцов. Записывают это так:

\\]

Или вот так:

\

Бывают и другие обозначения — тут всё зависит от предпочтений лектора/ семинариста/ автора учебника. Но в любом случае со всеми этими $\left$ и ${{a}_{ij}}$ возникает одна и та же проблема:

При чтении лекций и учебников ответ будет казаться очевидным. Но когда на экзамене перед вами — только листик с задачей, можно переволноваться и внезапно запутаться.

Поэтому давайте разберёмся с этим вопросом раз и навсегда. Для начала вспомним обычную систему координат из школьного курса математики:

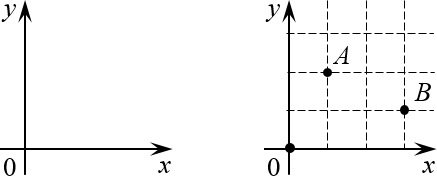Введение системы координат на плоскости

Помните её? У неё есть начало координат (точка $O=\left( 0;0 \right)$) оси $x$и $y$, а каждая точка на плоскости однозначно определяется по координатам: $A=\left( 1;2 \right)$, $B=\left( 3;1 \right)$ и т.д.

А теперь давайте возьмём эту конструкцию и поставим её рядом с матрицей так, чтобы начало координат находилось в левом верхнем углу. Почему именно там? Да потому что открывая книгу, мы начинаем читать именно с левого верхнего угла страницы — запомнить это легче лёгкого.

Но куда направить оси? Мы направим их так, чтобы вся наша виртуальная «страница» была охвачена этими осями. Правда, для этого придётся повернуть нашу систему координат. Единственно возможный вариант такого расположения:

Наложение системы координат на матрицу

Теперь всякая клетка матрицы имеет однозначные координаты $x$ и $y$. Например запись ${{a}_{24}}$ означает, что мы обращаемся к элементу с координатами $x=2$ и $y=4$. Размеры матрицы тоже однозначно задаются парой чисел:

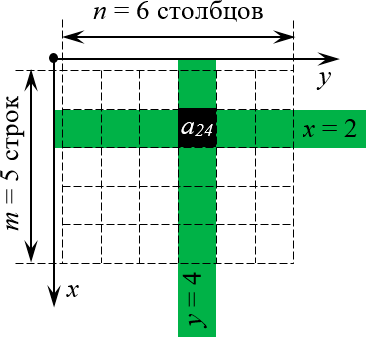Определение индексов в матрице

Просто всмотритесь в эту картинку внимательно. Поиграйтесь с координатами (особенно когда будете работать с настоящими матрицами и определителями) — и очень скоро поймёте, что даже в самых сложных теоремах и определениях вы прекрасно понимаете, о чём идёт речь.

Разобрались? Что ж, переходим к первому шагу просветления — геометрическому определению определителя.:)

Особенности модуля матрицы

Определитель матрицы является важным показателем, который характеризует свойства данной матрицы. Модуль определителя позволяет определить, насколько матрица «растягивает» пространство, образованное ее столбцами или строками.

Особенности модуля матрицы включают следующее:

Свойства модуля матрицы
Описание
Значение отлично от нуля
Если модуль матрицы отличен от нуля, то это означает, что матрица обратима и можно найти ее обратную матрицу.
Значение равно нулю
Если модуль матрицы равен нулю, то это означает, что матрица невырожденная и необратима. В этом случае система линейных уравнений, связанная с данной матрицей, может иметь бесконечное количество решений.
Значение больше нуля
Если модуль матрицы больше нуля, то это означает, что матрица является положительно определенной

Это важное свойство матрицы в линейной алгебре и теории оптимизации.
Значение меньше нуля
Если модуль матрицы меньше нуля, то это означает, что матрица является отрицательно определенной. Это также важное свойство матрицы и может использоваться в различных областях, например, в физике.

Таким образом, модуль матрицы позволяет определить ряд важных свойств и характеристик данной матрицы, которые могут быть полезными в различных областях науки и техники.

Матрица переноса

Матрица переноса выглядит так:

где X, Y, Z — это значения, которые мы хотим добавить к нашему вектору.

Значит, если мы захотим перенести вектор (10, 10, 10, 1) на 10 юнитов в направлении X, то мы получим:

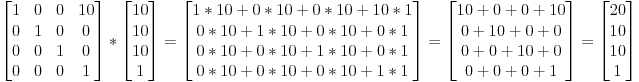
… получим (20, 10, 10, 1) однородный вектор! Не забывайте, что 1 в параметре w, означает позицию, а не направление и наша трансформация не изменила того, что мы работаем с позицией.

Теперь посмотрим, что случится, если вектор (0, 0, -1, 0) представляет собой направление:

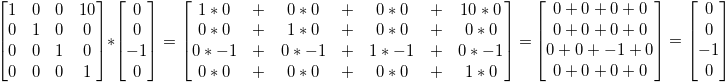
… и получаем наш оригинальный вектор (0, 0, -1, 0). Как было сказано раньше, вектор с параметром w = 0 нельзя перенести.

И самое время перенести это в код.

В C++, с GLM:

В GLSL:

По факту, вы никогда не будете делать это в шейдере, чаще всего вы будете выполнять glm::translate() в C++, чтобы вычислить матрицу, передать ее в GLSL, а уже в шейдере выполнить умножение

Случай переменной правой части

А теперь рассмотрим вот такое уравнение:

\

Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.

Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней — мы уже знаем, что модуль не может быть равен отрицательному числу.

А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».

Таким образом, сформулируем правило для произвольных функций $f\left( x \right)$ и $g\left( x \right)$ :

\

Применительно к нашему уравнению получим:

\

Ну, с требованием $2x\ge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.

Поэтому решим-ка само уравнение:

\

Ну и какой их этих двух корней удовлетворяет требованию $2x\ge 0$? Да оба! Поэтому в ответ пойдут два числа: $x=2$ и $x={2}/{5}\;$. Вот и всё решение.:)

Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:

\

Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:

\

И решается оно точно так же:

\

С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:

\

Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:

\

Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:

\

\

Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.

Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:

\

Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:

\

\

Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3}\;$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:

\

Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:

\

Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:

\

Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.

Умножение вектора на матрицу

Наконец,
рассмотрим умножение вектора на матрицу. Это также можно записать двумя
способами:

или

Для реализации
первого способа, зададим одномерный вектор и двумерную матрицу:

a = np.array(1,2,3)
b = np.arange(4,10).reshape(3,2) # матрица 3x2

И, затем,
воспользуемся уже знакомой нам функцией dot:

np.dot(a, b) # array()

При такой
записи, когда одномерный массив записан первым аргументом, а матрица – вторым,
получаем умножение вектора-строки на матрицу, то есть, первый способ.

Для реализации
второго способа аргументы нужно поменять местами: сначала указать матрицу, а
затем, вектор. Но, если мы сейчас это сделаем с нашими массивами, то получим
ошибку:

np.dot(b, a) # несогласованность размеров

Дело в том, что
массив a должен
представлять вектор длиной два элемента, так как матрица b имеет размер в
3 строки и 2 столбца:

Определим массивa в два элемента
и умножим на матрицу b:

a = np.array(1, 2)
np.dot(b, a) # array()

Получаем
вектор-строку (одномерный массив) как результат умножения

Обратите внимание,
по правилам математики вектор aдолжен быть вектором-столбцом, то есть,
быть представленным в виде:

a.shape = -1, 1 # вектор-столбец 2x1

Но мы
использовали вектор-строку. В NumPyтак тоже можно делать и это не приведет
к ошибке. Результат будет именно умножение матрицы как бы на вектор-столбец. Ну
а если использовать вектор-столбец, то и на выходе получим вектор-столбец:

np.dot(b, a) # вектор-столбец 3x1

Этого же результат можно достичь, используя оператор @ (перегрузка функции matmul):

a @ b # вектор-столбец 3x1

Результат будет
тем же. Вот так в NumPyвыполняется умножение матриц, векторов и
вектора на матрицу.

Алгебраический метод нахождения модуля матрицы

Один из методов нахождения модуля матрицы является алгебраический метод. Он основан на вычислении детерминанта матрицы.

Для того чтобы найти модуль матрицы с помощью алгебраического метода, нужно выполнить следующие шаги:

1. Найти определитель матрицы.
2. Если определитель положительный, то модуль матрицы равен самому определителю.
3. Если определитель отрицательный, то модуль матрицы равен абсолютному значению определителя.

Алгебраический метод нахождения модуля матрицы является одним из самых простых и универсальных методов. Он позволяет быстро найти модуль матрицы любого порядка.

Например, для матрицы размером 3×3:

1	2	-3
4	-5	6
-7	8	9

Определитель этой матрицы равен: 1*(-5)*9 + 2*6*(-7) + (-3)*4*8 — (-3)*(-5)*(-7) — 2*4*9 — 1*6*8 = -90.

Так как определитель отрицательный, модуль этой матрицы равен 90.

Геометрический метод нахождения модуля матрицы

Для матрицы с числовыми элементами существует несколько способов нахождения ее модуля. Один из таких способов — геометрический метод.

Геометрический метод нахождения модуля матрицы основан на представлении матрицы как линейного отображения векторов. Модуль матрицы можно определить как наибольшее значение, на которое матрица умножает некоторый вектор, при условии, что модуль этого вектора равен 1.

Для нахождения модуля матрицы с помощью геометрического метода следует выполнить следующие шаги:

1. Выбрать произвольный вектор (допустим, вектор размерности n), модуль которого равен 1.
2. Умножить этот вектор на матрицу и найти модуль полученного вектора.
3. Повторить шаг 2 для нескольких случайных векторов и выбрать наибольшее значение полученного модуля.

Таким образом, модуль матрицы можно определить как максимальное значение модуля, полученного вектором при его умножении на матрицу.

Геометрический метод нахождения модуля матрицы может быть полезным при решении различных задач в линейной алгебре и математическом анализе. Он позволяет определить, насколько сильно матрица изменяет векторы при своем действии на них.