Основные понятия векторной алгебры

Особенности длины вектора

Особенности длины вектора включают:

Положительность: длина вектора всегда является положительным числом или нулем. Даже если вектор направлен в обратную сторону, его длина будет положительной.
Зависимость от координат: длина вектора зависит от координат его начальной и конечной точки. Изменение какой-либо из этих координат приведет к изменению длины вектора.
Выражение через компоненты: длину вектора можно выразить через компоненты вектора с использованием теоремы Пифагора в трехмерном пространстве или теоремы Пифагора для произвольных размерностей.
Соотношение скалярного произведения: длина вектора может быть выражена через скалярное произведение самого вектора на себя.

Определение и измерение длины вектора являются важными векторными операциями и широко используются в геометрии, физике и других науках. Знание особенностей длины вектора позволяет более полно понять его свойства и использовать векторные операции для решения различных задач.

Модуль или абсолютная величина вектора

Модуль или абсолютная величина вектора представляет собой его длину, которая определяется по формуле:

Двумерный пространство:	\|a\| = √(a_x)2 + (a_y)2
Трехмерное пространство:	\|a\| = √(a_x)2 + (a_y)2 + (a_z)2

Где a_x, a_y, a_z представляют собой координаты вектора в соответствующих осях. Модуль вектора всегда является положительным числом или нулем, но никогда не может быть отрицательным.

Модуль вектора имеет важное значение при решении задач по физике и математике. Он позволяет определить длину перемещения, скорость и ускорение, а также установить равенство или неравенство между векторами

Благодаря модулю вектора можно производить его нормирование, то есть приводить вектор к единичной длине.

Модуль вектора также позволяет определить перпендикулярность двух векторов. Если модуль вектора равен нулю, значит он является нулевым вектором, который не имеет направления и считается коллинеарным любому другому вектору.

Неотрицательность длины вектора

Длина вектора определяется как квадратный корень из суммы квадратов его составляющих. Таким образом, все компоненты вектора возводятся в квадрат, суммируются, и затем из полученной суммы берется квадратный корень.

Такое определение длины вектора обладает следующими особенностями:

Квадратная корень всегда дает неотрицательное значение, даже если вектор имеет отрицательные компоненты.
Если вектор состоит из нулевых компонент, его длина будет равна нулю.
Длина вектора может быть равной нулю только в случае, когда сам вектор также равен нулевому вектору.

Таким образом, неотрицательность длины вектора является важным свойством, которое следует учитывать при работе с векторами и их длинами.

Геометрическая интерпретация длины вектора

Геометрически, длина вектора представляет собой расстояние от начала координат до конца вектора в пространстве. Она может быть вычислена с помощью формулы, которая основана на теореме Пифагора. Для двумерного пространства формула имеет вид:

|AB| = √((x2 — x1)^2 + (y2 — y1)^2)

где (x1, y1) и (x2, y2) — координаты начала и конца вектора, соответственно.

Геометрическая интерпретация длины вектора позволяет наглядно представить, насколько «длинным» или «коротким» является вектор. Она также позволяет определить направление вектора, так как длина вектора всегда положительна.

Длина вектора имеет важное значение во многих областях, включая математику, физику и компьютерную графику. Например, вектоная алгебра и геометрия используют длину вектора для определения углов между векторами и вычисления скалярных произведений

Таким образом, понимание геометрической интерпретации длины вектора является важным аспектом, позволяющим более глубоко и точно изучить свойства и особенности векторов.

Определение вектора и его роль в математике и физике

Вектор является одним из основных понятий в математике и физике. Он представляет собой величину, которая имеет не только численное значение, но и направление. Вектор может быть представлен как стрелка, направление которой указывает на направление вектора, а длина стрелки — на величину вектора.

Векторы используются для описания и решения широкого спектра задач в различных областях науки, включая физику, математику, инженерию и компьютерную графику. Они являются важным инструментом для моделирования и анализа различных физических и математических явлений.

Векторы могут быть складываться и вычитаться друг из друга, умножаться на число, а также выполнять другие операции. Их свойства позволяют определять их сумму, разность, угол между векторами, проекцию и многое другое. Векторы также удобно представлять в матричном виде, что позволяет использовать их в различных математических операциях.

В физике, векторы используются для описания физических величин, которые имеют как величину, так и направление. Например, вектор скорости описывает скорость движения тела и включает в себя информацию о его направлении. Вектор силы указывает на направление и величину силы, действующей на объект.

В математике, векторы используются для решения геометрических задач, анализа данных, решения линейных уравнений и многих других задач. Они играют важную роль в линейной алгебре, геометрии и векторном анализе.

Изучение векторов является неотъемлемой частью программы математического и физического образования. Понимание и использование векторов позволяет анализировать и решать сложные проблемы, связанные с движением, силами, силовыми полями, построением и разложением векторов и многими другими задачами.

Свойства линейных операций[править]

Коммутативность сложения векторовАссоциативность сложения векторов

Сложение векторов коммутативно: a+b=b+a{\displaystyle \mathbf {a} +\mathbf {b} =\mathbf {b} +\mathbf {a} }.

Сложение векторов ассоциативно: (a+b)+c=a+(b+c){\displaystyle (\mathbf {a} +\mathbf {b} )+\mathbf {c} =\mathbf {a} +(\mathbf {b} +\mathbf {c} )}.

Прибавление нулевого вектора к любому не меняет последнего: a+=a{\displaystyle \mathbf {a} +\mathbf {0} =\mathbf {a} }.
Очевидно, OA→+AA→=OA→{\displaystyle {\overrightarrow {OA}}+{\overrightarrow {AA}}={\overrightarrow {OA}}}.

Для любого вектора a=AB→{\displaystyle \mathbf {a} ={\overrightarrow {AB}}} существует вектор −a=BA→{\displaystyle -\mathbf {a} ={\overrightarrow {BA}}} такой, что a+(−a)={\displaystyle \mathbf {a} +(-\mathbf {a} )=\mathbf {0} } или AB→+BA→=AA→={\displaystyle {\overrightarrow {AB}}+{\overrightarrow {BA}}={\overrightarrow {AA}}=\mathbf {0} }.

Умножение вектора на число ассоциативно: (αβ)a=α(βa){\displaystyle (\alpha \beta )\mathbf {a} =\alpha (\beta \mathbf {a} )}.
Умножение вектора на число дистрибутивно относительно сложения чисел: (α+β)a=αa+βa{\displaystyle (\alpha +\beta )\mathbf {a} =\alpha \mathbf {a} +\beta \mathbf {a} }.

Доказательство сводится к перечислению всех возможных знаков α{\displaystyle \alpha } и β{\displaystyle \beta }, в каждом случае утверждение очевидно.

Дистрибутивность умножения векторов относительно сложения

Умножение вектора на число дистрибутивно относительно сложения векторов: α(a+b)=αa+αb{\displaystyle \alpha (\mathbf {a} +\mathbf {b} )=\alpha \mathbf {a} +\alpha \mathbf {b} }.
Это следует из подобия треугольников △OAB{\displaystyle \triangle OAB} и △OA′B′{\displaystyle \triangle OA’B’} на рисунке.

Очевидно, умножение на единицу не меняет вектор: 1a=a{\displaystyle 1\mathbf {a} =\mathbf {a} }.

Примечаниеправить

В алгебре изучаются так называемые алгебраические структуры. Это множества математических объектов, для которых определены некоторые операции, удовлетворяющие некоторым системам аксиом.

Пример такой структуры, изучаемой в линейной алгебре, — так называемое векторное (линейное) пространство. Это множество векторов, для которых определены операции сложения и умножения на элементы некоторого поля (например, поля вещественных чисел), причем эти операции удовлетворяют указанным выше свойствам.

В линейной алгебре изучаются общие свойства таких множеств, их элементы (их называют абстрактными векторами) не обязаны быть геометрическими векторами (хотя чаще всего именно их приводят в качестве наглядного примера).

В аналитической геометрии векторы нужны, в первую очередь для введения системы координат (см. ниже). Благодаря этому удается описать геометрические фигуры при помощи аналитических формул.

Единичные векторы

Вектор с длиной равной единице называют единичным вектором. Его также принято называть нормализованным вектором. Единичные векторы полезны тогда, когда вы имеете дело с направлением.

Нормализованный вектор

Нормализованный вектор получают путем уменьшения его длины до единицы с сохранением его направления. Это делается путем деления каждого из его компонентов на некую длину:

Существует общий способ, который обеспечивает операцию «нормализации» для и :

Отражение

Обычно единичные векторы используют для обозначения нормалей. Нормальный вектор прямой — это единичный вектор, направленный перпендикулярно к поверхности, определяющий ее направление. Они обычно используются для освещения, столкновений и других операций, связанных с поверхностями.

Например, представьте, что у нас есть движущийся мяч, который бы отскакивал от стены или другого объекта:

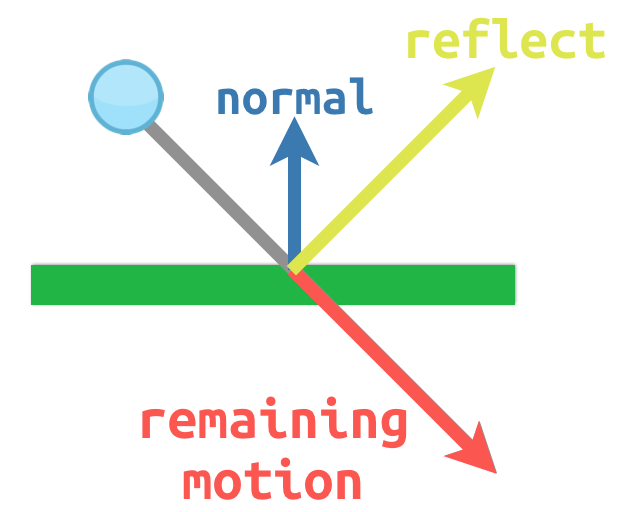
Нормаль поверхности имеет значение (0, -1), потому что это горизонтальная поверхность. Когда шар сталкивается c поверхностью, мы берем его оставшееся движение (значение, когда он касается поверхности) и отражаем его с помощью нормали. В Godot класс имеет метод для обработки этого. Ниже пример на GDScript, диаграммы представленной выше, используя :

Скалярное произведение (Dot product)

Скалярное произведение — это операция двух векторов, результатом которой является скаляр (произведение величин этих векторов, умноженное на косинус угла между ними). Скаляр является одним из наиболее важных понятий в линейной алгебре, но часто понимается неправильно. В отличие от вектора, который содержит длину и направление, скалярное значение содержит только длину.

Формула скалярного произведения имеет две общие формы:

а также:

Однако в большинстве случаев проще всего использовать встроенный метод. Заметим, что порядок двух векторов не имеет значения:

Скаляр наиболее полезен при использовании единичных векторов, из первой формулы видно, что все сводится к нахождению . Это означает, что мы можем использовать скаляр, чтобы узнать что-то об угле между двумя векторами:

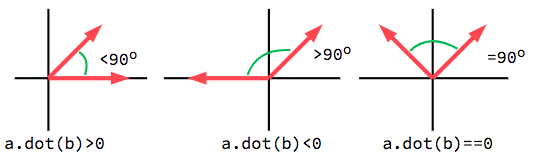
При использовании единичных векторов результат всегда будет находиться между значением (180°) и (0°).

Угол обзора

Мы можем использовать эффект «угла обзора», чтобы определить, обращен ли объект лицом к другому объекту. На приведенном ниже рисунке игрок пытается уйти от зомби и . Предположим, что угол обзора зомби , могут ли они видеть игрока?

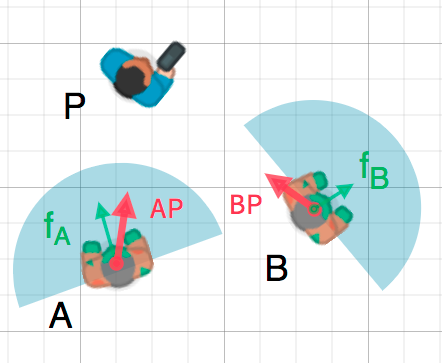
Зеленые стрелки и представляют собой единичные векторы, обозначающие направления движения зомби, а синий полукруг представляет собой поле зрения. Для зомби А находим вектор направления — используя действие находим вектор указывающий на игрока и далее нормализуем его. Если угол между найденным вектором и единичным вектором меньше , тогда зомби заметит игрока.

В коде это будет выглядеть так:

Векторное произедение

Также как и скалярное произведение, векторное произведение это операция над двумя векторами. Хотя в результате векторного произведения вы получаете вектор с направлением перпендикулярным обоим, его длина зависит от их относительного угла. Если два вектора параллельны, в результате вы получите нулевой вектор.

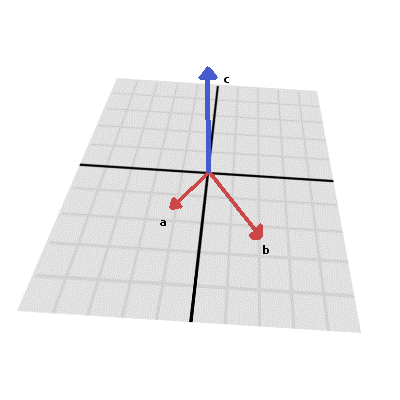
Векторное произведение выглядит следующим образом:

С помощью Godot вы можете использовать встроенный метод:

Расчет нормали

Одним из распространенных способов использования векторного произведения является расчет нормали к поверхности. Направления, в которых «смотрит» та или иная поверхность. Если у нас есть треугольник , мы можем использовать векторное произведение для нахождения двух ребер (B — A) и (C — A). Используя векторное произведение , находим вектор, перпендикулярный им обеим: т. е. перпендикулярный плоскости треугольника, также называемый «нормалью к плоскости».

Вот функция вычисления нормали треугольника:

Ось вращения

В разделе «Скалярное произведение» мы увидели, как его можно использовать для определения угла между двумя векторами. Однако в 3D этой информации недостаточно. Нам также нужно знать, об оси вращения. Мы можем найти ее, применив векторное произведение текущего направления “взгляда” и направления цели. Полученный перпендикулярный вектор и будет является осью вращения.

Как обратить линейную зависимость?

Линейная зависимость является состоянием, при котором один вектор может быть выражен линейной комбинацией других векторов. Однако иногда возникает необходимость обратить линейную зависимость и преобразовать ее в линейную независимость.

Существует несколько способов обратить линейную зависимость:

Добавление нового вектора: Добавление нового вектора, который не выражается линейной комбинацией имеющихся векторов, может привести к линейной независимости.
Удаление избыточного вектора: Если имеется набор векторов, один из которых может быть выражен линейной комбинацией остальных, то удаление этого избыточного вектора преобразует линейную зависимость в линейную независимость.
Применение линейных преобразований: Применение линейных преобразований, таких как повороты, отражения или масштабирование, может изменить линейную зависимость векторов и привести к линейной независимости.

Важно отметить, что обращение линейной зависимости может быть не всегда возможным или же может привести к потере информации. Поэтому в каждом конкретном случае необходимо проводить анализ и выбирать наиболее подходящий метод для обращения линейной зависимости

Усиление взаимосвязей между переменными

Взаимосвязи между переменными играют важную роль в анализе данных и машинном обучении. Более сильные и значимые взаимосвязи позволяют получить более точные и надежные результаты. В этом разделе разберем несколько способов усиления взаимосвязей между переменными.

1. Корреляционный анализ

Корреляционный анализ позволяет определить степень взаимосвязи между двумя переменными. Для этого используется коэффициент корреляции, который может принимать значения от -1 до 1. Значение 1 означает положительную линейную взаимосвязь, -1 — отрицательную линейную взаимосвязь, а 0 — отсутствие линейной взаимосвязи.

2. Преобразование переменных

Иногда преобразование переменных может помочь усилить взаимосвязи между ними. Например, можно применить логарифмическое преобразование, чтобы сгладить асимметричные распределения данных или уменьшить влияние выбросов.

3. Создание новых переменных

Создание новых переменных на основе существующих также может помочь улучшить взаимосвязи между переменными. Например, можно создать переменную, равную произведению двух других переменных, если есть предположение о существовании нелинейной зависимости.

4. Разделение данных

Иногда разделение данных на подвыборки может помочь выявить более сильные взаимосвязи. Например, можно разделить данные на две группы в зависимости от какого-то фактора и проанализировать взаимосвязи внутри каждой группы.

5. Использование дополнительных источников данных

Если взаимосвязи между переменными не оказываются достаточно сильными, можно обратиться к дополнительным источникам данных. Например, можно исследовать доступные статистические данные, опросы или провести эксперимент, чтобы получить дополнительную информацию о взаимосвязях между переменными.

Вывод

Усиление взаимосвязей между переменными может помочь улучшить точность и надежность анализа данных. Корреляционный анализ, преобразование переменных, создание новых переменных, разделение данных и использование дополнительных источников данных — это некоторые из способов усиления взаимосвязей

Важно учитывать контекст и специфику задачи при выборе и применении этих методов

Матрицы

Можно показать, что любую линейную функцию \(f: \mathbb{R}^n \to \mathbb{R}^m\) можно представить в следующем виде:

Матрицы ввели просто как очень компактную запись этих коэффициентов \(a_{ij}\).

Каждой линейной функции \(f\) из \(\mathbb{R}^n\) в \(\mathbb{R}^m\) соответствует какая-то матрица \(A\) размера \(n \times m\) (первое число это количество строк, второе — столбцов) и наоборот. Элемент на пересечении \(i\)-ой строки и \(j\)-го столбца будем обозначать \(A_{ij}\). Не перепутайте.

Если вектор — это упорядоченный набор скаляров, то матрицу можно рассматривать как вектор векторов. Вектор, в частности, можно представить как матрицу, у которой одна из размерностей равна единице — тогда его называют вектор-столбец либо вектор-строка.

Ещё есть тензоры — ими называют все объекты ещё более высокого порядка: векторы матриц (трёхмерный тензор), матрицы матриц (четырёхмерный тензор) и векторы матриц матриц и так далее.

У тензоров есть своя интересная алгебра, но в контекстах, в которых с ними сталкивается обычный программист, никакая алгебра, как правило, не подразумневается, и этот термин используется лишь потому, что в словосочетании «многомерный массив» слишком много букв.

Матричное умножение

Пусть линейной функции \(f\) соответствует матрица \(A\), а функции \(g\) соответствует матрица \(B\). Тогда композиции этих функций \(h = f \circ g\) будет соответствовать произведение \(C\) матриц \(A\) и \(B\), определяемое следующим образом:

Читатель может убедиться в этом, расписав, какие коэффициенты получаются, если формулы из \(g\) подставить в \(f\).

При перемножении матриц руками удобно думать так: элемент на пересечении \(i\)-го столбца и \(j\)-той строки — это скалярное произведение \(i\)-той строки \(A\) и \(j\)-того столбца \(B\). Заметим, что это накладывает ограничение на размерности перемножаемых матриц: если первая матрица имеет размер \(n \times k\), то вторая должна иметь размер \(k \times m\), то есть «средние» размерности обязательно должны совпадать.

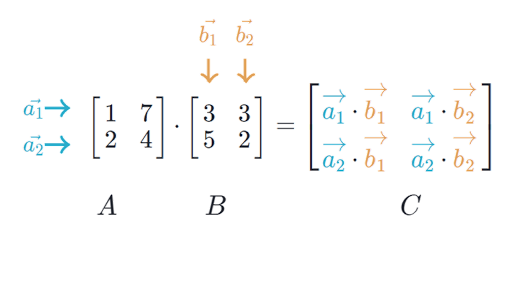
Исходное выражение для \(f(x)\) теперь можно компактно записать как \(f(x) = Ax\) вместо \(m\) уравнений с \(n\) слагаемыми в каждом.

Напишем функцию, реализующую матричное умножение:

Такая реализация хоть и наиболее простая, но не оптимальная ввиду особенностей работы кэша (см. раздел «Оптимизации матричного умножения»).

Свойства матриц

К матрицам не нужно относиться как к табличкам, в которых стоят какие-то числа. Каждой матрице соответствует какая-то линейная функция, как-то преобразующая вектора. Центральными объектами линейной алгебры являются именно линейные функции, а не матрицы.

Благодаря этому взаимно однозначному соотношению все ранее упомянутые свойства линейных функций переносятся и на матрицы:

Сумма матриц \(A\) и \(B\) тоже является матрицей: \(C = A+B: \; C_{ij} = A_{ij} + B_{ij}\).
Сумма матриц коммутативна: \(A+B = B+A\).
Сумма матриц ассоциативна: \((A+B)+C = A+(B+C)\).
Умножение матриц ассоциативно: \((AB)C = A(BC) = ABC\).
Умножение матриц в общем случае не коммутативно.

Есть специальная матрица \(I\) (иногда обозначается \(E\)), которая называется единичной и относительно умножения ничего не делает, то есть ведёт себя как единица. У неё единицы на главной диагонали и нули вне неё:

Некоторые линейные функции обратимы (например, поворот на угол), некоторые — необратимы (например, проекция). Понятие обратимости можно продолжить и на матрицы.

Определение. Матрица \(A\) является обратимой, если существует матрица \(A^{-1}\) такая, что \(A \cdot A^{-1} = A^{-1} \cdot A = I\).

Из формулы следует, что матрица \(A\) должна быть квадратной, но этого не всегда достаточно. У неквадратных матриц обратных матриц не существует. Обратную матрицу можно находить за \(O(n^3)\) методом Гаусса, который будет рассмотрен чуть позже.

Примеры матриц

Матрица «увеличь всё в два раза»:

Матрица «поменяй \(x\) и \(y\) местами»:

Матрица поворота на угол \(\alpha\) на плоскости:

Матрица проецирования на плоскость \(xy\) в трёхмерном пространстве:

Линейная зависимость: основные принципы линейной алгебры

Линейная зависимость является одним из ключевых понятий в линейной алгебре. Она описывает отношения между векторами в линейном пространстве. Линейная зависимость возникает, когда один вектор может быть выражен в виде линейной комбинации других векторов.

Основные принципы линейной зависимости:

Если существует нестандартное решение линейного уравнения, то векторы, определяющие это решение, линейно зависимы.
Если векторы линейно зависимы, то хотя бы один из них может быть выражен в виде линейной комбинации остальных векторов.
Если векторы линейно независимы, то ни один из них не может быть выражен в виде линейной комбинации остальных векторов.
Если векторы линейно зависимы, то хотя бы один из них является линейной комбинацией остальных векторов.

Для определения линейной зависимости векторов можно использовать матрицы и определители. Если векторы являются строками или столбцами матрицы, то они линейно зависимы, если определитель этой матрицы равен нулю.

Линейная зависимость играет важную роль в линейной алгебре. Она позволяет решать системы линейных уравнений, описывать пространства и многое другое. Понимание основных принципов линейной зависимости является фундаментальным для работы с линейной алгеброй.

Конечномерные пространства

конечномерным

основную теорему о линейной
зависимости

Масштабирование одного из векторов базиса. Возьмём какое-нибудь число
и умножим на него какой-нибудь вектор . Полученная система
векторов будет базисом
наравне с прежней. Почему? Потому что любой вектор пространства по-прежнему
будет представим в виде линейной комбинации этих векторов, и по-прежнему
единственным образом. Действительно, пусть в старом базисе произвольный
вектор представлялся в виде

Тогда в новом базисе он будет представляться в виде

где . И представление это по-прежнему единственно, ведь будь
их два, представлений в исходном базисе тоже было бы два (достаточно было бы
умножить -е коэффициенты этих двух представлений на , чтобы получить
коэффициенты двух представлений того же самого вектора в старом базисе).
Прибавление к одному из векторов базиса другого, умноженного на число.
Возьмём какое-нибудь число (теперь никто не запрещает ему быть нулём,
хотя случай с нулём тривиален и неинтересен) и вместо вектора
«подсунем» в базис вектор , остальные векторы оставив
без изменения. Новая система векторов
тоже будет базисом.
Проверим это. Пусть какой-либо вектор представлялся в старом базисе в
виде

Тогда в новом базисе он примет вид

Это несложно проверить, подставив вместо сумму ,
раскрыв пару скобок и сократив пару слагаемых. Совершенно аналогично можно
получить представление вектора в прежнем базисе, зная представление в
новом. Значит, представление в новом базисе всегда существует и всегда
единственно, как и представление в прежнем базисе.
Перестановка двух векторов базиса местами. Ну тут всё очевидно.

основную теорему о
линейной зависимостив любом конечномерном линейном пространстве
все базисы состоят из одного и того же количества векторов

нулевые

если
есть некоторый базис из векторов, то никакого базиса из векторов
существовать не может

основная теорема о линейной зависимости

размерностью

Во-вторых, норма матрицы

Сначала мы введем норма матриц в математике, то есть независимо от того, какая дисциплина объединяется. Отказ Отказ Например матрицаA =

2.1 Матрица1Норма

Матрица1Норма, колонна и норма, а именно:Элементы каждого столбца матрицы абсолютно оценены, а затем максимум, (столбец и максимум), вышеупомянутая матрицаAиз1Фан сначала получитьМаксимальный конечный результат:9，MATLABКод реализован как:norm（A，1）；

2.2 Матрица2Норма

Матрица2Номер, количество спектров, а именно:матрицаATAATAМаксимальная оценка функции Откройте квадратный корень, вышеупомянутая матрицаAиз2Окончательный результат нормы:10.0623，MATLABКод реализован как:norm（A，2）；

2.3 Бесконечная норма матрицы

Бесконечная норма, ряд и норма матрицы, а именно:Элементы каждой строки матрицы абсолютно оценены, а затем максимум, (строки и макс), вышеуказанная матрицаAиз1Фан сначала получитьМаксимальный конечный результат:16，MATLABКод реализован как:norm（A，inf）；

Далее мы должны представить низкий ранг машинного обучения, редким и т. Д., Обычно имеющие ядерные нормы,L0Норма,L1Норма (иногда многие люди также называют1Норма, это делает новичок легко смущенным),L21Норма (иногда также называется2Норма),FНорма…Приведенная выше норма состоит в том, чтобы решить новые определения нормы, предложенные в реальной задаче, отличной от передних матричных норм.

2.4 Количество ссылок

Количество ядерных ссылок:Особое значение матрицы (матрицаsvdРазложение), эта норм может быть использована для экспрессии (потому что минимальная ядерная норма, эквивалентная рангому рангому рангом матрицы минимизации), вышеупомянутая матрицаAКонечный результат:10.9287， MATLABКод реализован как:sum(svd(A))

2.5 МатрицаL0Норма

МатрицаL0Норма матрицы:Количество элементов, обычно используемых для выражения редкого,L0Меньшая нормаЧем больше элементов, тем более редкий, вышеуказанная матрицаAКонечный результат:6

2.6 МатрицаL1Норма

МатрицаL1Нормативно: абсолютное значение каждого элемента в матрице, этоL0Самая предпочтительная поверхность нормы, поэтому она также может представлять собой редкий, вышеупомянутая матрицаAКонечный результат:22，MATLABКод реализован как:sum(sum(abs(A)))

2.7 МатрицаFНорма

МатрицаFНорма,FrobeniusНорма, а именно:,Сумма слоев квадрата матрицы, и она часто называют матрицей.L2Норма, его преимущество — это выпуклая функция, может быть направлена, легко рассчитать, вышеуказанная матрицаAКонечный результат:10.0995，MATLABКод реализован как:norm（A，‘fro’）

2.8 МатрицаL21Норма

МатрицаL21НормаL1с участиемL2Норма нормы).

Сначала возьмите каждый список, как подразделение, спроситеКаждый столбецF.(Можно считать вектором 2Норма)
Тогда результат будет полученпроситьL1 НОРМ(1 можно считатьНорма)

MATLABКод реализован как: norm(A(:,1),2) + norm(A(:,2),2) + norm(A(:,3),2)

матрицаA =-12-34-66Конечный результат: 17.1559

Когда минимальная функция целевой функции (функция потери) требуется в выделении функции, необходимо доставлять всю формулу.

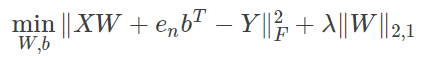
Как быть матрицейL2,1Норма руководства?

1.Вектор

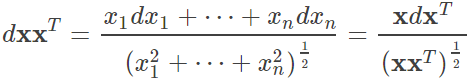
Итак, руководство необходимости

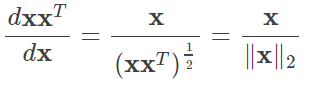
2.Матрица ищет

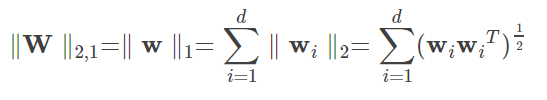
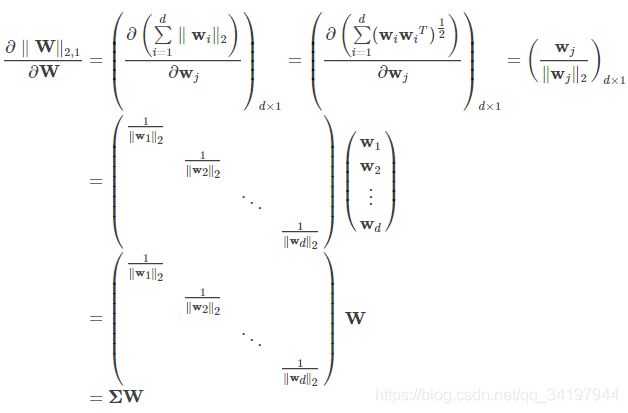
Что такое линейная зависимость?

Линейная зависимость — это понятие в линейной алгебре, которое описывает отношение между векторами в пространстве. Когда векторы линейно зависимы, это означает, что один или несколько векторов могут быть выражены как линейная комбинация других векторов.

Формально, векторы v₁, v₂, …, v_n в пространстве называются линейно зависимыми, если существуют коэффициенты c₁, c₂, …, c_n, не все из которых равны нулю, такие что:

c₁v₁ + c₂v₂ + … + c_nv_n = 0

Если такие коэффициенты существуют, то говорят, что векторы линейно зависимы. Если же такие коэффициенты не существуют, то векторы называются линейно независимыми.

Можно представить линейную зависимость и в графическом виде. Если два вектора коллинеарны и лежат на одной прямой, они линейно зависимы. Если они не коллинеарны и направлены в разные стороны, они также линейно зависимы. Но если векторы имеют разные направления и не лежат на одной прямой, они будут линейно независимыми.

Понятие линейной зависимости широко используется в математике и физике. Например, в анализе данных и машинном обучении, линейная зависимость векторов может означать мультиколлинеарность, что может привести к проблемам при решении систем линейных уравнений или при обучении моделей машинного обучения.