Что означает свойство геометрии

Важность изучения геометрии для развития мышления.

Геометрия – это одна из важнейших наук, которая оказывает существенное влияние на развитие человеческого мышления. Она изучает фигуры, пространства, отношения между ними, способы их измерения и многое другое. Именно благодаря геометрии люди начинают думать аккуратнее, логичнее и аналитичнее.

Первые представления о геометрии можно обнаружить в древности, где её основные понятия использовались в архитектуре, физике и других научных областях. Еще Аристотель называл геометрию первым упорядочением наших знаний об искусственной форме. Сегодня же, мы можем сказать, что геометрия помогает людям понимать тот факт, что все в нашем мире имеет форму и размер и может быть описано математическими терминами.

Математический анализ контекстов и пространств с помощью геометрических понятий помогает развивать различные критические навыки мышления. Геометрия даёт возможность увидеть все объекты и предметы вокруг нас в новом свете, основанном на логике и систематизации. Её изучение помогает развить пространственное воображение, а также укрепить логическое мышление, что может привести к глубокому и продолжительному развитию головного мозга.

Кроме этого, геометрия может стать дополнительным и важным инструментом для учеников изучающих точные науки. Она является неотъемлемой частью науки о пространстве, измерениях и отношениях. И вместе с алгеброй, она может помочь при решении сложных проблем, связанных с физическими явлениями и математическими моделями.

Обучение геометрии способствует развитию творческого мышления у школьников. Она позволяет формировать умственные карты воображаемых объектов, и улучшает навыки абстрактного мышления и умения видеть решения задач из разных углов. Возможность рассмотреть характеристики и свойства объектов, которые находятся в другом измерении, что помогает лучше понимать, что происходит в нашем мире, как и почему он функционирует.

Кроме вышеупомянутых преимуществ, изучение геометрии также помогает укрепить знания о других ключевых темах, таких как физика, география, астрономия и другие науки. Геометрия может существенно помочь при изучении этих областей знания, так как она позволяет увидеть связи между объектами, их координаты и широту, а также получать информацию о других параметрах, которые могут быть полезными при решении сложных проблем.

Итак, можно заключить, что изучение геометрии необходимо не только для профессиональных математиков и ученых, но и для обычных людей, которые хотят развивать свои мыслительные способности и увидеть все объекты и предметы вокруг них в новом свете. Геометрия учит нас различным навыкам, которые необходимы для успешной работы и эффективного функционирования в современном мире.

Функциональное применение геометрии в нашей жизни.

Геометрия – это наука о пространственной форме, размерах и относительном расположении объектов. Она играет важную роль в нашей жизни, ведь без использования геометрии невозможно представить себе многие сферы деятельности, начиная от архитектуры и дизайна и заканчивая техническими науками.

Архитектура – одна из областей, где геометрия существенно влияет на результат. Архитекторы используют принципы геометрии, чтобы создать красивые, эргономические и стабильные здания. Они определяют форму и размеры всех элементов здания, начиная с основания и заканчивая крышей. Для создания качественной и безопасной конструкции необходимо учесть все аспекты геометрии, начиная от расположения отдельных элементов здания и заканчивая расположением окон и дверей.

Дизайн также невозможен без геометрии. Дизайнеры используют геометрические принципы, чтобы создать привлекательный и эстетичный дизайн. Геометрия помогает здесь определить размеры и пропорции объектов, которые будут использованы в дизайне, включая формы, геометрические фигуры, линии и текстуры.

Кроме того, геометрия играет важную роль в инженерных и технических науках. В этих областях геометрия используется для проектирования и создания машин, устройств, инструментов и технологических наладок. Различные формы и геометрические фигуры используются для создания точных и эффективных деталей, необходимых для производства тех или иных устройств. Если бы не геометрия, то эти устройства и машины были бы неэффективными, а часто и просто невозможными для создания.

Одна из важных областей применения геометрии – это также картография. Эту науку волнует проблема описания и изображения географических объектов на картах. Они могут быть представлены в различных проекциях и в различном масштабе, а для этого требуются знания в геометрии.

Другая важная область, использующая геометрию – это небольшая группа наук, изучающих движение, как например, механика. Движение предметов в трехмерном пространстве в значительной степени определяется с помощью геометрических расчетов. Эти расчеты используются для определения скорости и положения объектов, а также их ускорения и действия внешних сил на них.

В медицине геометрия также играет важную роль. На основе геометрических принципов создаются модели человеческих тканей, что позволяет лучше понимать как они работают. Это, в свою очередь, помогает лучше понимать механизмы различных болезней и разрабатывать эффективные методы лечения.

Таким образом, геометрия, казалось бы, абстрактная наука, оказывается крайне применимой во многих областях нашей жизни. От архитектуры и дизайна до медицины и производства – геометрия повсюду. Без нее мы жили бы в менее качественном мире, так как геометрия – это основа любой точной и эффективной работы.

Свойства и особенности прямой

Свойства прямой:

1. Прямые, параллельные друг другу, имеют одинаковый угловой коэффициент.
2. Прямая, перпендикулярная другой прямой, имеет угловой коэффициент, равный обратному значению углового коэффициента первой прямой.
3. Прямая, пересекающая оси координат, имеет точки пересечения с осью ординат (y-осью) и осью абсцисс (x-осью).
4. Две прямые, наклонные друг к другу, не пересекаются и никогда не становятся параллельными.

Прямые используются в различных областях математики, физики и инженерии. Например, они применяются для построения графиков функций, в теории вероятностей, в компьютерной графике и в конструировании. Знание свойств и особенностей прямой позволяет анализировать и решать задачи, связанные с ее поведением и взаимодействием с другими объектами.

Бесконечность

В математике, бесконечность представляет собой концепцию, которая используется для описания того, что не имеет конечного значения или размера. Например, множество всех натуральных чисел представляет собой бесконечное множество. Бесконечность также используется в анализе и геометрии для описания пределов функций и бесконечно малых величин.

В физике, бесконечность может быть связана с понятием бесконечно больших или бесконечно малых значений. Например, в теории относительности, события в черной дыре могут быть описаны как имеющие «бесконечную кривизну» или «бесконечную гравитацию».

В философии и религии, бесконечность может быть связана с понятием божественности и абсолютной реальности. Некоторые философы считают бесконечность фундаментальной характеристикой мира и существования, в то время как другие рассматривают бесконечность как нечто потенциальное или недостижимое для человеческого понимания.

Примеры бесконечности можно найти во многих аспектах жизни. Например, при рассмотрении числовых последовательностей или делении одного числа на другое, бесконечность может возникнуть в виде бесконечной десятичной дроби. Также, если мы начнем счиать натуральные числа, мы никогда не достигнем конечного числа, так как их количество бесконечно.

Бесконечность – это концепция, которая вызывает интерес и вопросы, и она продолжает быть исследуемой и обсуждаемой в различных областях знания

Неожиданно, бесконечность может быть и в малейших вещах, например, в атомах и молекулах, что указывает на ее важность и сложность

Единственность

Уникальность контента означает, что тексты, изображения и другие элементы сайта не должны иметь аналогов в интернете. Первый и самый важный принцип создания уникального контента — это его оригинальность. Повторение или копирование контента других сайтов может негативно сказаться на репутации и ранжировании сайта в поисковых системах.

Оригинальный контент также влияет на пользовательский опыт. Когда посетитель впервые заходит на сайт и видит интересную и уникальную информацию, его интерес и вовлеченность повышаются. Кроме того, уникальный контент способствует развитию бренда и созданию узнаваемого стиля, который может быть ассоциирован с конкретным сайтом или компанией.

Для создания уникального контента важно продемонстрировать свою экспертизу и предлагать посетителям новую и ценную информацию

Также можно использовать интерактивные элементы, такие как опросы, голосования или калькуляторы, чтобы привлечь и удержать внимание пользователей

Важно отметить, что единственность контента не должна быть ограничена только текстом. Веб-сайты могут быть уникальными в своем дизайне, структуре и продукте, которые предлагают

Идеально, когда все аспекты сайта работают вместе, чтобы создать полностью уникальный и оригинальный опыт для посетителей.

В итоге, создание уникального контента и продемонстрирование единственности веб-сайта — это одна из ключевых стратегий, которая помогает достичь успеха в онлайн-среде.

Невероятные свойства геометрических фигур.

Геометрические фигуры – это структуры, которые обладают определенными математическими свойствами и характеристиками. Они используются во всех областях науки и технологий, таких как архитектура, инженерное дело, физика и многие другие. Геометрические фигуры обладают удивительными свойствами, и в этой статье мы рассмотрим некоторые из них.

Круг

Одной из наиболее известных геометрических фигур является круг. Она обладает многими удивительными свойствами, начиная от того, что все точки на ее периметре находятся на одинаковом расстоянии от ее центра. В дополнение к этому, круг обладает максимальной площадью для заданного периметра, что делает его идеальной формой для многих объектов и проектов.

Треугольник

Другой известной геометрической фигурой является треугольник. Он обладает некоторыми особенными свойствами, одно из которых заключается в том, что сумма всех углов в треугольнике равна 180 градусам. Кроме того, треугольник может быть прямоугольным, равнобедренным или равносторонним.

Квадрат

Квадрат имеет четыре равные стороны, а углы все одинаковые и равны 90 градусам. Это свойство делает квадрат идеальной формой для многих приложений, включая строительство и архитектуру.

Прямоугольник

Прямоугольник имеет две пары сторон, равных между собой, и каждый из его углов равен 90 градусам. Он обладает несколькими важными свойствами, такими как возможность вычислить его площадь и периметр.

Ромб

Ромб имеет четыре стороны, каждая из которых равна другой, а углы все равны между собой. Это свойство делает ромб идеальной формой для некоторых приложений, таких как проектирование катера или корабля. Кроме того, ромб обладает центральной симметрией, что делает его очень эстетичным.

Трапеция

Трапеция – это геометрическая фигура, у которой есть две пары сторон, одна из которых параллельна другой. Она используется во многих областях в качестве базовой формы для создания различных компонентов. У трапеции есть несколько важных свойств, например, ее площадь может быть вычислена, и она представляет собой идеальную форму для создания арки или перехода между двумя поверхностями.

Геометрические фигуры обладают многими удивительными свойствами и характеристиками, которые могут быть использованы во многих областях науки и технологий. В этой статье мы рассмотрели некоторые из основных геометрических фигур и их свойства. Надеемся, что это поможет вам лучше понять и оценить значение геометрии в нашей жизни.

Определение и основные характеристики

Основные характеристики прямой включают:

1. Бесконечность: прямая не имеет начала или конца и распространяется в обе стороны бесконечно.
2. Прямое направление: прямая простирается в одном направлении без изгибов или поворотов.
3. Единство: на любой прямой линии можно выбрать две любые различные точки, и все остальные точки на прямой линии лежат между этими двумя точками.
4. Отсутствие ширины и толщины: прямая линия имеет нулевую ширину и толщину, она представляет собой идеально тонкую линию без объема.

Примеры:

— Нить, которую мы растягиваем между двумя точками;

— Луч света, который движется в прямом направлении;

— Грани куба или параллелограмма, которые являются прямыми линиями.

Геометрическое определение

Прямая представляет собой наиболее простой элементарный объект в геометрии. Ее основная особенность заключается в том, что прямая имеет одну и только одну прямую между любыми двумя ее точками. Это означает, что прямая также является кратчайшим расстоянием между двумя точками в геометрии.

Прямая может располагаться в плоскости или в трехмерном пространстве. В плоскости она представляет собой прямую линию, которая не имеет ширины или толщины. В трехмерном пространстве прямая представляет собой объект без объема.

Примеры прямых могут включать границы сторон геометрических фигур, таких как треугольник или квадрат. Они также могут быть видимыми линиями на рисунке или шкале. В реальном мире мы можем наблюдать прямые на дорогах, равномерно отрезанных сторонах зданий или линиях на спортивных полях.

Геометрическое определение прямой является основой для понимания многих других понятий в геометрии, таких как отрезки, углы, окружности и многое другое. Оно является ключевым элементом в изучении геометрии и находит применение в различных областях науки и техники.

Алгебраическое определение

Ax + By + C = 0

где A, B и C — константы, а x и y — переменные. Такое уравнение называется уравнением прямой в общем виде.

Коэффициенты A и B определяют наклон прямой, а коэффициент C — расстояние от начала координат до прямой.

Например, уравнение 2x + 3y — 6 = 0 задает прямую, проходящую через точку (3, 0) и (0, 2).

Алгебраическое определение позволяет выразить прямую в виде уравнения, что упрощает анализ прямой и позволяет решать задачи, связанные с ее свойствами и взаимодействием с другими объектами в пространстве.

История развития планиметрии

Планиметрия – одна из основных разделов геометрии, изучающая геометрические фигуры и пространственные объекты, которые лежат в одной плоскости. В основе планиметрии лежат такие понятия, как точка, прямая, плоскость, угол, фигура и другие.

История развития планиметрии уходит в древность. Уже в течение многих веков до нашей эры, древние культуры вели измерения земли, строили здания и суда, разрабатывали карты. Древние Египтяне, Вавилоняне, граждане Древней Греции и Рима активно использовали планиметрию в своих практических нуждах.

Одной из первых написанных работ, посвященной геометрии и планиметрии, является «Элементы» Евклида – каноническое произведение, которое оказало огромное влияние на развитие математики и геометрии в частности. Содержание «Элементов» было активно изучено и обсуждалось многими учеными и математиками в течение следующих веков.

В средние века планиметрия и геометрия в целом переживали некоторый спад, связанный с упадком научного исследования в течение этого периода. Однако, даже в течение этого времени, некоторые ученые продолжали развивать идеи и принципы планиметрии.

В 17 и 18 веках планиметрия и геометрия вновь стали активно развиваться. В эти века были созданы работы великих математиков, таких как Рене Декарт, Иоганн Кеплер и Леонард Эйлер, которые внесли значительный вклад в развитие планиметрии. Были разработаны новые методы и алгоритмы решения геометрических задач, установлены новые теоремы и принципы.

В 19 и 20 веках планиметрия и геометрия стали предметами активного исследования и развития, в особенности в связи с развитием математического аппарата и применением геометрии в других областях, таких как физика и инженерия. На основе планиметрии были разработаны новые методы анализа и решения геометрических проблем, которые имели практическое применение.

• Сводка:
  1. Планиметрия развивалась с древних времен;
  2. Одной из первых работ по планиметрии были «Элементы» Евклида;
  3. В средние века геометрия и планиметрия переживали спад;
  4. В 17-18 веках планиметрия вновь стала активно развиваться;
  5. В 19-20 веках планиметрия стала предметом активного исследования и развития.

История развития планиметрии продолжается и в наше время, когда геометрия и планиметрия используются в различных научных и технических областях, а также являются одним из основных курсов в школьной и высшей математической программе.

Примеры использования проецирующей прямой

1. Архитектура и дизайн

Проецирующая прямая широко используется в архитектуре и дизайне для создания перспективных рисунков и планов зданий. Например, архитектор может использовать проецирующую прямую, чтобы получить проекцию фасада здания на плоскость. Это помогает представить, как здание будет выглядеть в реальности и определить пропорции и расположение деталей.

2. Графика и компьютерное моделирование

Проецирующая прямая применяется в графике и компьютерном моделировании для создания трехмерных изображений. Например, в трехмерной графике проецирующая прямая может использоваться для определения положения точки или объекта на двумерном экране. Это позволяет создавать реалистичные изображения, которые отображают то, как объекты выглядят из разных ракурсов.

3. Конструкционная геометрия

Проецирующая прямая находит применение в конструкционной геометрии для решения различных задач. Например, она может использоваться для нахождения пересечения прямой и плоскости или для определения положения точки на плоскости по ее проекции на прямую. Это помогает инженерам и архитекторам проводить точные измерения и вычисления, что является важным в строительстве и проектировании.

Пример использования проецирующей прямой в архитектуре	Пример использования проецирующей прямой в графике	Пример использования проецирующей прямой в конструкционной геометрии

Это лишь некоторые примеры использования проецирующей прямой. В реальности ее применение может быть намного шире и разнообразнее, в зависимости от предметной области и задачи, которую нужно решить.

Построение горизонтальной прямой с помощью графических инструментов

Для построения горизонтальной прямой на чертеже или компьютерном графическом редакторе можно использовать различные инструменты.

Во многих графических программных инструментах есть инструмент «Линия» или «Инструмент рисования прямой». Для построения горизонтальной прямой нужно выбрать этот инструмент и нарисовать линию, удерживая клавишу Shift на клавиатуре. Клавиша Shift принуждает инструмент рисования рисовать только горизонтальные, вертикальные или диагональные линии.

Также можно использовать инструмент «Прямоугольник» или «Инструмент квадрат». Для построения горизонтальной прямой нужно нарисовать очень узкий и высокий прямоугольник, удерживая клавишу Shift. Затем стоит удалить вертикальные стороны этого прямоугольника, оставив только горизонтальную линию.

Если вы используете программу, которая поддерживает работу с векторной графикой, то можно использовать инструмент «Кривая Безье» или «Кривая Безье с фиксированными концами». Для построения горизонтальной прямой нужно создать точки начала и конца линии по одной высоте и затем настроить кривую таким образом, чтобы она проходила строго горизонтально.

Вариантов и инструментов для построения горизонтальной прямой с помощью графических инструментов достаточно много. Выбор инструмента зависит от того, какая программа используется, какие навыки имеются у пользователя и какие требования предъявляются к результату.

Выбор подходящей поверхности для рисования

Для успешного построения прямой линии важно выбрать подходящую поверхность для рисования. Ведь комфортность и точность результата зависят от выбранного материала

1. Бумага: Один из наиболее распространенных вариантов для рисования прямых линий

Но следует обратить внимание на тип бумаги, так как избыток картона или грубая текстура могут затруднить трассировку

2. Листок в клеточку: Полезен, если вам требуется рисовать прямые линии, которые должны быть ровными и симметричными. Клетки помогут вам поддерживать правильное распределение линий и точность изображения.

3. Доска для рисования: Идеально подходит для выполнения больших прямых линий или чертежей. Доски из ДВП или фанеры предоставляют ровную поверхность и удобство в использовании.

4. Цифровой планшет: В настоящее время все более популярны цифровые инструменты для рисования. Они позволяют создавать точные прямые линии с использованием программного обеспечения и специальных инструментов

Однако, перед использованием, следует обратить внимание на настройки и калибровку планшета для оптимальных результатов

Независимо от выбранной поверхности, важно начинать рисовать прямую линию с достаточныма опорами. Использование линеек, траспарантов или других руководящих инструментов поможет вам получить более точный и профессиональный результат

Уравнение прямой с угловым коэффициентом

Записываем уравнение вида: \;

x — значение, которое принимается, как переменное;

к — простое действительное число, является показателем углового коэффициента;

b — действительное число.

Угол наклона на плоскости в системе координат — угол, который берет свой отсчет значений от направления с положительным знаком до прямой, которая направлена против хода часовой стрелки.

Угол будут считать нулевым, если прямая линии, имеют параллельное расположение относительно оси абсцисс либо совпадает с ней по расположению. Угол принимает значения, согласно интервалу (0, \).

Формула

Угловой коэффициент — значение тангенса угла наклона этой же прямой линии.

В случае, когда прямая линия параллельная другой оси, ординат, то принято считать, что угловой коэффициент не определяется. И соответствует интервалу бесконечности.

График функции будет возрастать, если значение коэффициента имеет положительное значение. Следовательно, убывание будет наблюдаться в противоположном значение, а именно с отрицательным значением.

На графиках показаны значения угловых коэффициентов и угол наклона. Когда есть разное расположение относительно осей.

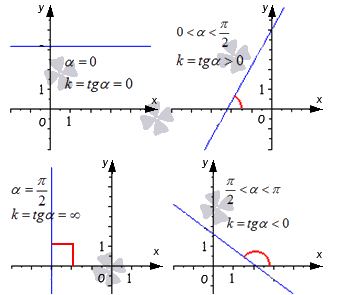
На примерах рассмотрим нахождение углового коэффициента. Для этого из прошлых тем, вспомним определение тангенса и его вычисление.

Пример №1:

Угол наклона прямой равен 120 градусов, относительно оси ох.

Нам нужно определить угловой коэффициент.

Применим известные нам формулы и подставим данные.

\

Следовательно правильный ответ задачи будет равняться \

Пример №2:

В этом примере нам уже известно значение углового коэффициента.

Нужно определить угол наклона, относительно прямой.  Для этого, нужно обязательно учитывать знак известного коэффициента. Если к>0, следует что угол будет острый и определяться как \.

Когда к<0, то угол будет характеризоваться как тупой. его значение определяется функцией: \.

Например, угловое значение равно 3.

Значение коэффициента является положительным, значит угол будет острый. Вычисляться он будет по формуле: \

Ответ задачи: \.

Пример №3:

Значение углового коэффициента имеет отрицательное число в виде дроби.  И равняется следующему значению: \

Для определения угла наклона, выполнить следующие действия: обозначим все значения. Угол наклона относительно оси имеет положительное значение. Следовательно формула для решения запишется следующим образом: \.

Подставим данные, которые заданы в условии задания:

\ответ будет \.

Пример №4:

Необходимо определить, относятся ли точки координат к прямой. Они равны: \. Уравнение прямой задано следующее: \.

Известные нам значения точек подставляем, в заданное уравнение прямой.

И получаем следующий вид формулы: \. Так после вычисления, мы получаем равенство, которое считается верным. Можно утверждать, что точка принадлежит прямой.

Далее подставляем значения второй точки в уравнение.

\ следовательно точка \ не относится к прямой и не лежит на ней.

Вывод решения: только первая точка относится к прямой и лежит на ней, а вторая равная (2;-2) — нет.

Пример №5:

Нужно найти уравнение прямой, которая проходит через значение точки \. Значение углового коэффициента — (-2).

Запишем условие : \

Следовательно необходимое уравнение прямой равно: \.

\

Искомое уравнение: \

Пример №6:

Составить уравнение прямой, проходящей через значение (-2;4). Угол наклона положительного направления равен \.

Решение необходимо начать с определения коэффициента угла.

\

Определив угловое значение, можно составить искомое уравнение вида: \