Ломаная линия: что это такое, виды и примеры

В геометрии

Коническое сечение

Вырожденная коника — это коническое сечение (плоская кривая второй степени , определяемая полиномиальным уравнением второй степени), которая не может быть неприводимой кривой.

• A точкой, является вырожденная окружность, а именно, радиус 0.
• Линия — это вырожденный случай параболы, если парабола находится на касательная плоскость. В инверсной геометрии линия является вырожденным случаем окружности с бесконечным радиусом.
• Две параллельные линии также образуют вырожденную параболу.
• A отрезок можно рассматривать как вырожденный случай эллипса, в котором малая полуось переходит в ноль, а фокусы переходят в конечных точек, а эксцентриситет переходит в единицу.
• Окружность можно представить как вырожденный эллипс, поскольку эксцентриситет приближается к нулю.
• Эллипс также может вырождаться в одну точку.
• A гипербола может вырождаться в две линии, пересекающиеся в точке, через семейство гипербол, имеющих эти линии как общие асимптоты.

Треугольник

A вырожденный треугольник имеет коллинеарные вершины и нулевую площадь и, таким образом, совпадает с отрезком, покрытым дважды (если три вершины не равны; в противном случае треугольник вырождается в одну точку). Если три вершины попарно различны, он имеет два угла 0 ° и один угол 180 °. Если две вершины равны, у него один угол 0 ° и два неопределенных угла.

Прямоугольник

• Отрезок линии — это вырожденный случай прямоугольника , длина стороны которого равна 0.
• Для любого непустого подмножества S ⊆ {1, 2,…, n} {\ displaystyle S \ substeq \ {1,2, \ ldots, n \}}, существует ограниченный выровненный по оси вырожденный прямоугольник

  R ≜ {x ∈ R n: xi = ci (для i ∈ S) и ai ≤ xi ≤ bi (для i ∉ S)} {\ displaystyle R \ Triangleq \ left \ {\ mathbf {x} \ in \ mathbb {R} ^ {n}: x_ {i} = c_ {i} \ ({\ text {for}} i \ in S) {\ text {и}} a_ {i} \ leq x_ {i} \ leq b_ {i} \ ({\ text {for}} i \ notin S) \ right \}}

  где x ≜ {\ displaystyle \ mathbf {x} \ треугольник q \ left }и ai, bi, ci {\ displaystyle a_ {i}, b_ {i}, c_ {i}}являются постоянными (с ai ≤ bi {\ displaystyle a_ {i} \ leq b_ {i }}для всех i {\ displaystyle i}). Количество вырожденных сторон R {\ displaystyle R}- это количество элементов подмножества S {\ displaystyle S}. Таким образом, может быть всего одна вырожденная «сторона» или целых n {\ displaystyle n}(в этом случае R {\ displaystyle R}сводится к одноэлементной точке).

Выпуклый многоугольник

A выпуклый многоугольник является вырожденным, если хотя бы две последовательные стороны совпадают хотя бы частично, или хотя бы одна сторона имеет нулевую длину, или хотя бы один угол равен 180 °. Таким образом, вырожденный выпуклый многоугольник с n сторонами выглядит как многоугольник с меньшим числом сторон. В случае треугольников это определение совпадает с тем, что было дано выше.

Выпуклый многогранник

A выпуклый многогранник вырожден, если либо две смежные грани копланарны, либо два ребра являются выровнен. В случае тетраэдра это эквивалентно тому, что все его вершины лежат в одной плоскости, что дает ему объем нуля.

Стандартный тор

В контекстах, где разрешено самопересечение, сфера представляет собой вырожденный стандартный тор, ось вращения которого проходит через центр образующий круг, а не за его пределами.

Свойства

Определение невырожденного треугольника в геометрии основано на том, что углы треугольника суммируются в 180 градусов, каждая сторона больше нуля, и сумма двух сторон всегда больше третьей стороны. Любая грань треугольника является отрезком, соединяющим две его вершины.

Примерами невырожденных треугольников могут служить треугольник со сторонами 3, 4 и 5, а также треугольник с углами 30, 60 и 90 градусов.

Равенство суммы углов треугольника 180 градусам.

Стандартное определение треугольника в геометрии — это фигура, образованная тремя сторонами и тремя вершинами. Каждая сторона соединяет две вершины, а каждый угол образуется двумя сторонами, исходящими из одной вершины. Углы треугольника также могут быть классифицированы как острые (меньше 90 градусов), прямые (равные 90 градусам) или тупые (больше 90 градусов).

Признак невырожденного треугольника — это условие, при котором сумма длин любых двух сторон треугольника всегда больше длины третьей стороны. Иначе говоря, треугольник должен быть «закрытой» фигурой, а не прямой линией или точкой.

Важным свойством невырожденного треугольника является равенство суммы углов треугольника 180 градусам. Это значит, что сумма всех внутренних углов треугольника равна 180 градусам. Например, если у нас есть треугольник с углами 60 градусов, 70 градусов и 50 градусов, то их сумма будет равна 180 градусам.

Сумма длин двух сторон треугольника всегда больше длины третьей стороны.

В геометрии треугольник представляет собой плоскую фигуру, образованную тремя отрезками, называемыми сторонами треугольника. Каждая сторона треугольника является гранью этой фигуры, а точки их пересечения – вершинами. Сумма длин двух сторон определенного треугольника всегда больше длины третьей стороны и служит важным признаком для определения невырожденного треугольника.

Позвольте рассмотреть пример, чтобы увидеть это свойство в действии. Предположим, что у нас есть треугольник с сторонами длиной 5, 7 и 10 единиц. Чтобы проверить, выполняется ли свойство суммы длин двух сторон, необходимо сложить длины двух самых коротких сторон:

Стороны треугольника	Сумма длин двух сторон
5, 7, 10	5 + 7 = 12

Как видим, сумма длин двух сторон треугольника равна 12. Затем сравниваем эту сумму с длиной третьей стороны:

Стороны треугольника	Сумма длин двух сторон	Длина третьей стороны
5, 7, 10	12	10

Как можно заметить, сумма длин двух сторон (12) больше длины третьей стороны (10), что подтверждает наше утверждение о том, что сумма длин двух сторон треугольника всегда больше длины третьей стороны.

Сумма длин двух сторон треугольника является важным свойством, она влияет на множество других характеристик треугольника, таких как его площадь, углы и отношения между сторонами.

Высоты треугольника пересекаются в одной точке — ортоцентре.

Одним из важных свойств треугольника является то, что все высоты треугольника пересекаются в одной точке, которая называется ортоцентром. Именно ортоцентр является точкой пересечения трех высот треугольника.

Ортоцентр имеет много геометрических свойств и является ключевой точкой в задачах треугольника. Он лежит внутри или на границе треугольника, в зависимости от его типа и положения высот. Более того, ортоцентр может быть использован для определения других важных элементов треугольника, таких как окружность Эйлера и описанная окружность.

Одно из основных свойств ортоцентра заключается в том, что отрезки, соединяющие ортоцентр с вершинами треугольника, перпендикулярны соответствующим сторонам. Это означает, что углы между сторонами треугольника и этими отрезками равны 90 градусам.

Еще одним важным признаком ортоцентра является его связь с площадью треугольника. Для любого треугольника, площадь треугольника ABC равна произведению половины основания BC на высоту, проведенную из вершины A:

SABC = 0.5 * BC * HA, где SABC — площадь треугольника ABC, BC — основание треугольника, HA — высота, проведенная из вершины A.

Таким образом, ортоцентр треугольника имеет большое значение и определение его свойств позволяет углубить понимание треугольника в геометрии. Благодаря своей особенной природе, ортоцентр является важным элементом в решении задач и определении основных характеристик треугольника.

Нормированное векторное пространство

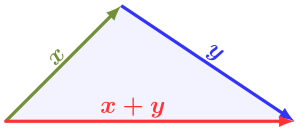Неравенство треугольника для норм векторов.

В нормированное векторное пространство V, одно из определяющих свойств норма это неравенство треугольника:

‖Икс+у‖≤‖Икс‖+‖у‖∀Икс,у∈V{ displaystyle displaystyle | x + y | leq | x | + | y | quad forall , x, y in V}

то есть норма не больше суммы норм двух векторов. Это также называется субаддитивность. Чтобы любая предлагаемая функция вела себя как норма, она должна удовлетворять этому требованию.

Если нормированное пространство евклидов, или, в более общем смысле, строго выпуклый, тогда ‖Икс+у‖=‖Икс‖+‖у‖{ Displaystyle | х + у | = | х | + | у |} если и только если треугольник, образованный Икс, у, и Икс + у, является вырожденным, то естьИкс и у находятся на одном луче, т.е. Икс = 0 или у = 0, илиИкс = α y для некоторых α > 0. Это свойство характеризует строго выпуклые нормированные пространства, такие как ℓ_п пространства с 1 < п < ∞. Однако есть нормированные пространства, в которых это неверно. Например, рассмотрим самолет с ℓ₁ норма ( Манхэттенское расстояние ) и обозначить Икс = (1, 0) и у = (0, 1). Тогда треугольник, образованныйИкс, у, и Икс + у, невырожден, но

‖Икс+у‖=‖(1,1)‖=|1|+|1|=2=‖Икс‖+‖у‖.{ Displaystyle | х + у | = | (1,1) | = | 1 | + | 1 | = 2 = | х | + | у |.}

Примеры норм

Абсолютное значение как норма для реальная линия. Чтобы быть нормой, неравенство треугольника требует, чтобы абсолютная величина удовлетворять для любых реальных чисел Икс и у:

|Икс+у|≤|Икс|+|у|,{ Displaystyle | х + у | Leq | х | + | у |,}

что он делает.

Доказательство:

−|Икс|≤Икс≤|Икс|{ displaystyle — left vert x right vert leq x leq left vert x right vert}

−|у|≤у≤|у|{ displaystyle — left vert y right vert leq y leq left vert y right vert}

После добавления

−(|Икс|+|у|)≤Икс+у≤|Икс|+|у|{ Displaystyle — ( влево верт х вправо верт + влево верт у вправо верт) Leq х + у Leq влево верт х вправо верт + влево верт у вправо vert}

Используйте тот факт, что |б|≤а⇔−а≤б≤а{ displaystyle left vert b right vert leq a Leftrightarrow -a leq b leq a}(с участием б заменяется Икс+у и а от |Икс|+|у|{ displaystyle left vert x right vert + left vert y right vert}), у нас есть

|Икс+у|≤|Икс|+|у|{ Displaystyle | х + у | Leq | х | + | у |}

Неравенство треугольника полезно в математический анализ для определения наилучшей верхней оценки размера суммы двух чисел в терминах размеров отдельных чисел.

Существует также более низкая оценка, которую можно найти с помощью обратное неравенство треугольника в котором говорится, что для любых действительных чисел Икс и у:

|Икс−у|≥||Икс|−|у||.{ displaystyle | x-y | geq { bigg |} | x | — | y | { bigg |}.}

Внутренний продукт как норма в внутреннее пространство продукта. Если норма возникает из внутреннего произведения (как в случае евклидовых пространств), то неравенство треугольника следует из Неравенство Коши – Шварца следующим образом: данные векторы Икс{ displaystyle x} и у{ displaystyle y}, и обозначив внутренний продукт как ⟨Икс,у⟩{ Displaystyle langle х, у rangle}:

‖Икс+у‖2{ Displaystyle | х + у | ^ {2}}	=⟨Икс+у,Икс+у⟩{ displaystyle = langle x + y, x + y rangle}
	=‖Икс‖2+⟨Икс,у⟩+⟨у,Икс⟩+‖у‖2{ displaystyle = | x | ^ {2} + langle x, y rangle + langle y, x rangle + | y | ^ {2}}
	≤‖Икс‖2+2|⟨Икс,у⟩|+‖у‖2{ Displaystyle Leq | х | ^ {2} +2 | langle x, y rangle | + | y | ^ {2}}
	≤‖Икс‖2+2‖Икс‖‖у‖+‖у‖2{ Displaystyle Leq | х | ^ {2} +2 | х | | у | + | у | ^ {2}} (по неравенству Коши – Шварца)
	=(‖Икс‖+‖у‖)2{ Displaystyle = влево ( | х | + | у | вправо) ^ {2}}.

Неравенство Коши – Шварца превращается в равенство тогда и только тогда, когда Икс и улинейно зависимы. Неравенство⟨Икс,у⟩+⟨у,Икс⟩≤2|⟨Икс,у⟩|{ displaystyle langle x, y rangle + langle y, x rangle leq 2 | langle x, y rangle |}превращается в равенство для линейно зависимых Икс{ displaystyle x} и у{ displaystyle y}тогда и только тогда, когда один из векторов Икс или у это неотрицательный скаляр другого.

Извлечение квадратного корня из окончательного результата дает неравенство треугольника.

п-норма: обычно используемой нормой является п-норма:

‖Икс‖п=(∑я=1п|Икся|п)1п ,{ Displaystyle | х | _ {p} = left ( sum _ {i = 1} ^ {n} | x_ {i} | ^ {p} right) ^ {1 / p} ,}

где Икс_я компоненты вектора Икс. Для п = 2 то п-норма становится Евклидова норма:

‖Икс‖2=(∑я=1п|Икся|2)12=(∑я=1пИкся2)12 ,{ Displaystyle | х | _ {2} = влево ( сумма _ {я = 1} ^ {п} | х_ {я} | ^ {2} вправо) ^ {1/2} = влево ( sum _ {i = 1} ^ {n} x_ {i} ^ {2} right) ^ {1/2} ,}

который Теорема Пифагора в п-размеры, очень частный случай, соответствующий внутренней норме продукта. Кроме случая п = 2, то п-норма не внутренняя норма продукта, потому что она не удовлетворяет закон параллелограмма. Неравенство треугольника для общих значений п называется Неравенство Минковского. Он принимает вид:

‖Икс+у‖п≤‖Икс‖п+‖у‖п .{ displaystyle | x + y | _ {p} leq | x | _ {p} + | y | _ {p} .}

Значение понятия «Невырожденный треугольник»

Невырожденный треугольник — это треугольник, который имеет конечные стороны и углы, а также положительную площадь. Такой треугольник является основным объектом изучения геометрии и математики.

Значит, треугольник, который не является невырожденным, будет иметь одну или несколько из следующих характеристик:

• Одна или несколько сторон имеют нулевую длину. В этом случае треугольник превращается в отрезок или точку.
• Одна или несколько сторон имеют отрицательную длину. Это может происходить, когда точки, задающие стороны треугольника, расположены в неправильном порядке.
• Сумма длин двух сторон меньше третьей стороны. Такой треугольник называется вырожденным, и он не может существовать в двумерном пространстве.
• Один или несколько углов равны 0 или 180 градусов. Такие углы называются вырожденными углами и не отличаются от прямой линии или плоскости.

Имея эти определения в виду, мы можем утверждать, что для треугольника с конечными сторонами и положительной площадью справедливо понятие «невырожденный треугольник». Это базовое понятие является основой для изучения свойств и характеристик треугольников в геометрии.

Основные характеристики невырожденного треугольника

Что значит невырожденный треугольник? Невырожденный треугольник — это треугольник, у которого все три стороны положительной длины и никакие три точки, задающие его вершины, не лежат на одной прямой.

Вот основные характеристики, которые отличают невырожденный треугольник:

• Три стороны: невырожденный треугольник имеет три стороны, каждая из которых имеет положительную длину и является отрезком прямой между двумя вершинами.
• Три вершины: треугольник имеет три вершины, которые являются точками пространства или плоскости. Вершины образуют углы друг с другом.
• Три угла: треугольник состоит из трех углов, которые образуются между сторонами. Сумма всех углов в невырожденном треугольнике равна 180 градусам.
• Площадь: невырожденный треугольник имеет площадь, которая можно вычислить с использованием формулы Герона или других методов.
• Периметр: периметр невырожденного треугольника — это сумма всех его сторон. Он также может быть вычислен с помощью известных значений длин сторон.

Невырожденный треугольник является одной из основных фигур в геометрии. Он имеет множество свойств и характеристик, которые могут быть использованы для изучения его свойств и применения в различных математических и физических задачах.

Различия невырожденного треугольника от вырожденного

Треугольник — это геометрическая фигура, состоящая из трех отрезков, которые соединяются между собой в трех точках. Однако не все треугольники являются невырожденными, и это имеет свои особенности и значения.

Невырожденный треугольник (также известный как обычный треугольник) — это треугольник, у которого все три стороны имеют разную длину и все три угла не равны нулю и не равны 180 градусов. Невырожденный треугольник значит, что он имеет достаточно размеров и формы, чтобы считаться полноценным и функциональным треугольником.

Основное отличие невырожденного треугольника от вырожденного заключается в его свойствах и определениях. Невырожденный треугольник имеет три разные стороны и три угла, которые в сумме равны 180 градусов. Каждая сторона невырожденного треугольника соединяет две точки, и каждый угол образуется между двумя сторонами. Такой треугольник может быть измерен и описан с помощью геометрических формул и правил.

В то же время, вырожденный треугольник имеет особые свойства и определения. Он представляет собой треугольник, у которого все три стороны соединены в одной точке, а все три угла равны нулю или 180 градусов. Это значит, что его стороны и углы не образуют полноценной фигуры у треугольника и не могут быть измерены с помощью геометрических формул.

Таким образом, различия между невырожденным и вырожденным треугольниками заключаются в их свойствах и определениях. Невырожденный треугольник является полноценной геометрической фигурой с тремя разными сторонами и углами в сумме, равной 180 градусов, в то время как вырожденный треугольник не обладает такими свойствами и не может быть измерен с помощью геометрических формул.

Способы определения типов невырожденных треугольников:

Способ 1: Определение по длинам сторон

Если треугольник имеет три стороны, причем каждая сторона неравна нулю, то его можно классифицировать по длинам сторон.

• Равносторонний треугольник — все стороны равны между собой.
• Разносторонний треугольник — все стороны различны.
• Равнобедренный треугольник — у треугольника есть две равные стороны.

Способ 2: Определение по углам

Углы треугольника также могут помочь определить его тип:

• Остроугольный треугольник — все углы треугольника острые (меньше 90 градусов).
• Прямоугольный треугольник — треугольник имеет один прямой угол (равный 90 градусов).
• Тупоугольный треугольник — треугольник имеет один тупой угол (больше 90 градусов).

Способ 3: Определение по соотношению длин сторон и углов

Существуют также более сложные условия, при которых возможно определение типа треугольника. Например, если известно, что сторона треугольника в 4 раза больше, чем ордината основания высоты, а один его угол составляет 60 градусов, то такой треугольник называется 30-60-90 треугольником.

Зная эти способы определения, можно точно классифицировать невырожденный треугольник по его свойствам и характеристикам.

Основные формулы

Для каждого треугольника существует набор формул, с помощью которых можно определить его элементы. Чаще всего приходится выяснять длины сторон, площадь, высоты и периметр. При этом если известны боковые грани, можно найти практически любые остальные параметры.

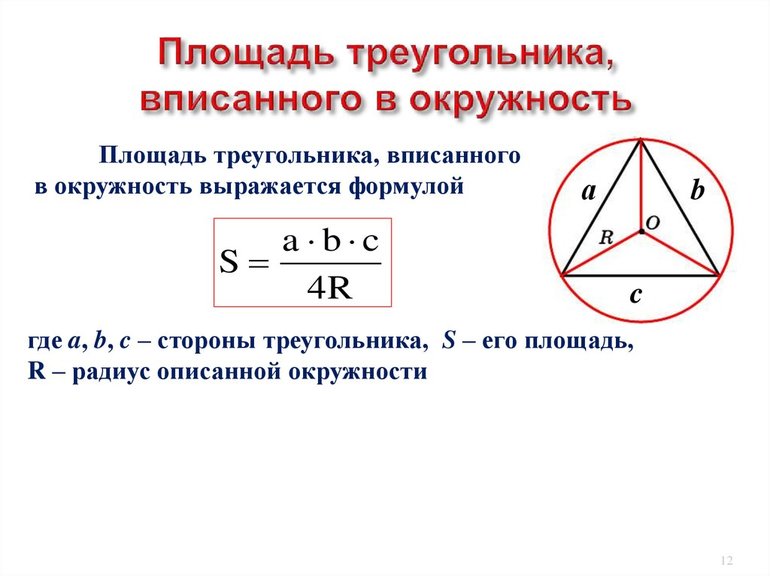
Вокруг правильной фигуры можно описать круг, причём окружность можно и вписать в середину. Что интересно, их центры совпадут между собой и с местом пересечения высот. В этом случае радиус внешнего круга равняется R = (a * √‎3) / 3 = a / 2 * sin (a), а внутреннего: r = (a * √‎3) / 6 = R / 2. Чтобы найти высоту, зная радиус, используют выражение: h = (3 *R) / 2. Кроме этой формулы, довольно часто применяют равенство, связывающее сторону и перпендикуляр: h = (a * √‎3) / 2.

Доказательство верности формулы для нахождения радиуса вписанной окружности можно построить исходя из выражения, справедливого к равнобедренной фигуре: r = b / 2 √(‎(2 a — b) / (2 a + b)). Так как стороны равны, то a = b. Получается, что r = a / 2 √‎(2a — a) / (2a + a) = (a / 2) * √‎(1 / 3) = a / (2 * √‎3) = (a √‎3) / 6.

Чтобы определить длину стороны, нужно знать высоту и теорему Пифагора. Согласно ей, квадрат гипотенузы находится как сумма квадратов высоты и длины разделённого основания. Применяя теорему к правильной фигуре, можно записать: AB2 = h2 + (AB / 2)2. Это равенство решают следующим образом: AB2 = h2 + AB2 / 22. Выражение можно преобразовать в вид: (3a2 / 4) = h 2 → a 2 = (4 * h2) / 3 → a 2 = √‎((4 * h2) / 3) → a = (2 * h) / √3.

Из других существующих формул можно перечислить те, что чаще всего применяют при решении примеров:

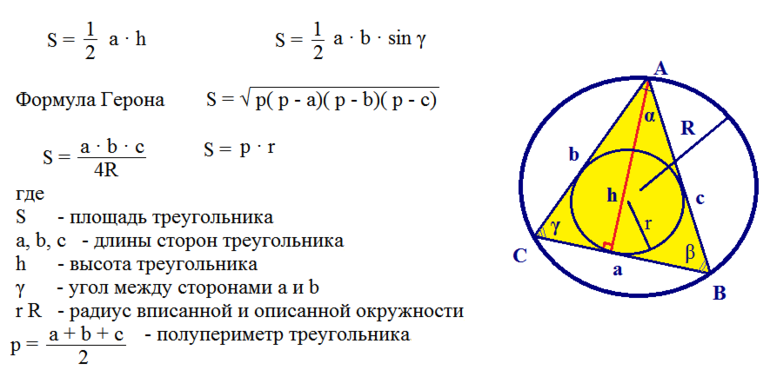
1. Площадь. Находят из выражения: S = (a 2 * √3) / 4. Вывести эту формулу довольно просто. Если взять за основу, что равенство для площади верно, то исходя из свойств фигуры можно записать: S = ½ * a2 * sin 60 = ½ * a2 * √3 / 2 = (√3 / 4) * a2. Что и следовало доказать.
2. Периметр. Чтобы его определить, нужно сложить длины всех сторон, но так как в правильной фигуре они равны, можно воспользоваться формулой: P = 3 * a.

Существуют ещё 2 значимые теоремы: косинусов и синусов. Согласно первой, квадрат стороны фигуры будет ранятся удвоенному произведению двух оставшихся отрезков и косинусу угла между ними, отнятому из суммы квадратов: a2 = b2 + c2 — 2 * b * c * cos (a). Согласно же второй, длины отрезков пропорциональны синусам углов, лежащих напротив: a / sin (a) = b / sin (b) = c / sinс.

Краткое описание

Специалисты называют ломаной ту геометрическую фигуру, которая представляет собой непрямую линию, состоящую исключительно из многочисленных соединённых отрезков. Учащимся нужно запомнить, что все эти фрагменты могут сходиться под абсолютно разными углами. Проще говоря, если есть даже самый маленький угол между двумя соединёнными отрезками, то это линия своеобразного ломаного типа.

Прямая тоже может состоять сразу из нескольких геометрических фрагментов, но угол их соединения приравнивается к нулю. Для избежания грубых математических ошибок нужно помнить, что ломаная линия отличается от кривой, так как отдельные отрезки представляют собой прямую линию, чего нельзя сказать о кривой.

В некоторых случаях пространственная ломаная может образовывать замкнутую фигуру. Но такая ситуация возможна только тогда, когда концы крайних отрезков совпадают, а также пересекают самих себя. Рассматриваемая в математике фигура состоит из вершин и отрезков, которые и соединяют эти вершины. Но в этом случае действует правило — два последних отрезка не должны лежать на одной прямой.

Сторонами или звеньями изогнутой линии принято называть составные отрезки. Минимальное количество звеньев — два. Специалисты привыкли называть чёрными точками конечные вершины ломаной линии. Чтобы графически всё выглядело правильно, необходимо использовать обозначения в соответствии с названиями задействованных вершин.

Если конечные вершины совпадают, тогда речь касается изогнутой замкнутой линии. В качестве примера можно рассмотреть многоугольник. Эта фигура представляет собой плоскую замкнутую ломаную, которая лишена каких-либо самопересечений. Вершины ломаной линии и её звенья относятся к многоугольнику. Если речь касается фигуры с тремя сторонами и вершинами, то это треугольник.

Немного сложнее разобраться с замкнутой ломаной и её четырьмя сторонами, так как это может быть прямоугольник, квадрат, параллелограмм, ромб и даже трапеция. Если фигура имеет пять или более сторон, то она называется n-угольником. Символ n указывает на точное число вершин.

Многоугольники

Многоугольник — это геометрическая фигура, которая характеризуется количеством углов и звеньев. Углы составлены парами звеньев замкнутой ломаной, сходящимися в одной точке. Звенья называются еще сторонами многоугольника. Общие точки двух отрезков называют вершинами многоугольника.

Количество звеньев или сторон в каждом многоугольнике соответствует количеству углов в нем же. Замкнутая ломаная из трех отрезков называется треугольником. Ломаная из четырех звеньев получила название четырехугольника. Фигура из пяти отрезков — пятиугольник и т. д.

Часть плоскости, которая ограничена замкнутой ломаной, называется плоским многоугольником. Другое ее название — многоугольная область.

Свойства

Ниже приведены основные свойства, общие для всех многоугольников:

1. Если вершины многоугольника служат концами одной стороны, их называют соседними. Если же вершины не прилежат к одной стороне, они несоседние.
2. Наименьшее количество сторон у многоугольника равняется трем. Однако треугольники, находясь рядом друг с другом, могут образовывать новые фигуры.
3. Если отрезок соединяет между собой несоседние вершины, он носит название диагонали.
4. Если фигура лежит относительно одной прямой в любой полуплоскости, она называется выпуклой. При этом прямая содержит в себе одну сторону фигуры и сама принадлежит полуплоскости. Выиграть в российских казино может каждый. Вероятность получения выигрыша с азартных игр зависит только от удачливости игрока. Чтобы увеличить шансы на победу, стоит выбирать слоты с высоким уровнем RTP и различными бонусными опциями. Если же в слоте есть джекпот, шансы на крупный денежный приз увеличиваются в несколько раз.
5. Угол, смежный внутреннему углу многоугольника при некоторой вершине, называется внешним.
6. Если все стороны и углы многоугольника равны, он называется правильным.

Треугольники

Треугольником в математике принято называть плоскую геометрическую фигуру, которая состоит из трех точек, не располагающихся на одной прямой. Эти точки соединены тремя отрезками.

Точки представляют собой вершины или треугольника, а отрезки — его стороны. Возле каждой из вершин образуется угол треугольника. Таким образом эта фигура имеет три угла, что видно из ее названия.

Различают следующие виды треугольников:

1. Равносторонние — все стороны их равны по длине.
2. Разносторонние — все стороны различаются по длине.
3. Равнобедренные — две стороны из трех имеют одинаковую длину.
4. Остроугольные — если все углы острые.
5. Прямоугольные — если имеется прямой угол.
6. Тупоугольные — если есть один тупой угол.

Четырехугольники

Плоская геометрическая фигура, имеющая четыре угла и четыре стороны, называется четырехугольником.

Если все углы у четырехугольника прямые — это прямоугольник.

Правильный четырехугольник носит название квадрата.

Определение и основные свойства

Невырожденный треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, называемые вершинами треугольника.

Основными свойствами невырожденного треугольника являются:

1. Сумма углов треугольника: Сумма всех внутренних углов треугольника равна 180 градусов. То есть, если обозначить углы треугольника как A, B и C, то A + B + C = 180°.
2. Стороны треугольника: Треугольник состоит из трех сторон, обозначаемых как a, b и c. Каждая сторона треугольника является отрезком, соединяющим две вершины треугольника.
3. Углы треугольника: Треугольник состоит из трех углов, обозначаемых как A, B и C. Углы треугольника могут быть различного размера, но их сумма всегда равна 180 градусов (свойство №1).
4. Высоты треугольника: Высоты треугольника — это перпендикулярные отрезки, проведенные из вершин треугольника к противолежащим сторонам. Высоты обозначаются как h_a, h_b и h_c.
5. Медианы треугольника: Медианы треугольника — это отрезки, соединяющие вершины треугольника с серединами противолежащих сторон. Медианы обозначаются как m_a, m_b и m_c.
6. Биссектрисы треугольника: Биссектрисы треугольника — это отрезки, проходящие через вершину треугольника и делящие противолежащий угол пополам. Биссектрисы обозначаются как bis_a, bis_b и bis_c.
7. Окружность, вписанная в треугольник: Это окружность, которая касается всех трех сторон треугольника. Центр вписанной окружности обозначается как I, а радиус — r.
8. Окружность, описанная вокруг треугольника: Это окружность, которая проходит через все три вершины треугольника. Центр описанной окружности обозначается как O, а радиус — R.

Эти основные свойства помогают в изучении и анализе треугольников, а также используются при решении задач и конструировании треугольников.

Связь невырожденного треугольника с другими геометрическими фигурами

Невырожденный треугольник обладает рядом свойств и связей с другими геометрическими фигурами:

1. Прямоугольный треугольник: Если один из углов невырожденного треугольника равен 90 градусов, то такой треугольник называется прямоугольным. В прямоугольном треугольнике один из углов является прямым углом, а вторые два угла являются остроугольными или тупыми. Такой треугольник имеет множество интересных свойств, включая теорему Пифагора.

2. Равносторонний треугольник: Если все стороны невырожденного треугольника равны между собой, то такой треугольник называется равносторонним. У равностороннего треугольника все три угла равны 60 градусам, и он обладает множеством уникальных свойств, таких как равенство высот, биссектрис и медиан.

3. Равнобедренный треугольник: Если две стороны невырожденного треугольника равны между собой, то такой треугольник называется равнобедренным. У равнобедренного треугольника два угла равны между собой, а оставшийся угол может быть разным. Такой треугольник обладает рядом интересных свойств, таких как равенство биссектрис, связанных с основанием треугольника, и равенство углов при вершине.

4. Треугольник равноугольный: Если все углы невырожденного треугольника равны между собой, то такой треугольник называется равноугольным или равнобедренным. В равноугольном треугольнике все углы равны между собой и равны 60 градусам. Такой треугольник обладает множеством интересных свойств, включая равенство высот, биссектрис и медиан.

5. Треугольник подобный: Невырожденный треугольник может быть подобным другому треугольнику, если их соответствующие углы равны между собой. Подобные треугольники имеют пропорциональные стороны и подобные углы, что позволяет строить аналогии в их свойствах и отношениях.

Эти связи невырожденного треугольника с другими геометрическими фигурами являются основой для решения геометрических задач и доказательства теорем. Они позволяют строить связи и обобщения между различными фигурами и углублять понимание геометрии.

Топ вопросов за вчера в категории образование

Образование 28.10.2023 10:34 2273 Угланова Яна.

Как решить: Для перевозки груза потребовалось 24 машины грузоподъём. 7,5 т?

Ответов: 1

Образование 31.08.2023 01:19 920 Романенкова Маша.

«Со своей стороны» выделяется запятыми или нет?

Ответов: 1

Образование 20.08.2023 17:20 991 Плотникова Юля.

Как правильно: «не подходит» или «неподходит»?

Ответов: 1

Образование 26.09.2023 09:48 1707 Сапроненков Евгений.

Какое проверочное слово к слову «облегчить» (облегчение)?

Ответов: 1

Образование 10.10.2023 17:31 984 Швецов Степан.

Какое проверочное слово к слову иссЯкать?

Ответов: 1

Образование 11.10.2023 21:09 1662 Ситникова Евгения.

Какое проверочное слово к слову ПРЕДПОЛАГАТЬ?

Ответов: 1

Образование 02.09.2023 05:24 1534 Салымгереев Акылбек.

Как правильно: по получении или по получению?

Ответов: 1

Образование 09.09.2023 09:10 2270 Дианочка Диана.

Какие фрукты начинаются на букву «Ф»?

Ответов: 1

Образование 07.11.2023 10:30 456 Ширяев Данил.

Какое проверочное слово к слову СОСТАВЛЯТЬ?

Ответов: 1

Образование 16.09.2023 23:41 2405 Ткачёв Витя.

Какое проверочное слово к слову ОГОРОД?

Ответов: 1

Остались вопросы?

Занимаетесь изучением математики или готовитесь к экзаменам? Найти ответы на многие вопросы по истории треугольников, их свойств и типов вы можете на сайте с видеоуроками http://interneturok.ru. Здесь собраны лекции по школьному курсу геометрии. Удобная система поиска на сайте поможет быстро найти и узнать, что такое вписанный треугольник, какими свойствами обладает равносторонний треугольник, теорема Пифагора и ее доказательство, первый, второй и третий признаки равенства треугольников и многое другое. Школьный курс геометрии разделен по классам. На портале вы найдете уроки за 7, 8, 9, 10 и 11 классы по геометрии. Видеоуроки четко структурированы по классам, темам и конкретным учебникам.