Деление чисел с остатком

Деление, модуль, отрицательные числа

Операция деления по модулю может быть немного запутанной, особенно когда дело касается отрицательных чисел. Рассмотрим, что происходит под капотом и какие результаты можно ожидать.

Деление по модулю (также известное как операция остатка) возвращает остаток от деления двух чисел. Например, если мы разделим число 10 на 3, то остаток будет равен 1, потому что 10 = 3 * 3 + 1. Операция остатка полезна во многих ситуациях, например, при проверке четности числа или при работе с календарями и временем.

Когда деление по модулю применяется к отрицательным числам, получаемые результаты могут вызвать некоторую путаницу. Результат зависит от языка программирования и конкретной реализации оператора. В некоторых случаях остаток может быть отрицательным числом.

Например, если мы разделим -10 на 3, то получим остаток -1. Это объясняется следующим образом: -10 = 3 * (-3) + (-1). В этом случае, операция деления по модулю возвращает тот остаток, который находится наиболее близко к нулю.

Однако, в других случаях, операция деления по модулю может возвращать только положительные остатки. Например, если мы разделим -10 на 3, то получим остаток 2. Это объясняется так: -10 = 3 * (-4) + 2. В этом случае, операция деления по модулю считается «правильной» в том смысле, что возвращает только неотрицательные результаты.

Если вы работаете с делением по модулю в своей программе, обратите внимание на форматирование результатов и ожидаемое поведение в отношении отрицательных чисел. Учтите, что результат может различаться в зависимости от языка, платформы или используемой библиотеки

Инкремент (++)/декремент (—)

Инкремент ++ (от англ. increment «увеличение») — операция, увеличивающая переменную на единицу. Обратную операцию называют декремент -- («уменьшение»).

Возвращаемое значение оператора ++ зависит от его позиции относительно операнда. Если поставить его перед операндом (префиксный оператор инкремента), то к операнду прибавляется единица, а результатом является увеличенное значение операнда. Если же он размещается после операнда (постфиксный оператор инкремента), то к операнду прибавляется единица, однако результатом является первоначальное значение операнда.
Так:

можно записать, как

В то время, как

эквивалентно

Рассмотрим различия между следующими двумя инструкциями:

Выполнить код »
Скрыть результаты

Внимание: Операнд инкремента (++)/декремента (—) должен быть значением (т.е. переменной, элементом массива или свойством объекта)

Код 7++ даст ошибку.

Декремент -- работает похоже, но в отличие от инкремента, вычитает единицу из числа.

Префиксный инкремент и декремент, согласно , имеют в инструкциях одинаковый приоритет и выполняются слева направо, например:

Выполнить код »
Скрыть результаты

Результат первого выражения равен 11 потому, что значение переменной уменьшается на единицу перед сложением. Результат второго выражения также равен 11 потому, что складываются уже измененные значения операндов.

Постфиксный декремент --, как и инкремент, указывается после переменной и выполняется после вычисления инструкции, которая его содержит:

Выполнить код »
Скрыть результаты

Результат первого выражения равен 12 потому, что переменная имеет первоначальное значение (2). Результат второго выражения равен 11 потому, что здесь используется уже уменьшенное значение (1).

Применение: Постфиксная форма отличается от префиксной тем, что возвращает старое значение своего аргумента, бывшее до увеличения (уменьшения).

Как вычислить Mod

Mod, или модуль, в математике обозначает остаток от деления. Вычислить Mod можно с помощью следующей формулы:

a mod b = a — b * floor(a/b)

где a — делимое, b — делитель, floor(a/b) — целая часть от деления.

Для примера, вычислим Mod для чисел 10 и 3:

1. 10 / 3 = 3, остаток 1
2. floor(10/3) = 3
3. a — (b * floor(a/b)) = 10 — (3 * 3) = 1

Таким образом, Mod для чисел 10 и 3 равен 1.

Для вычисления Mod также можно использовать модифицированную формулу:

a mod b = ((a % b) + b) % b

где a — делимое, b — делитель, % — оператор остатка от деления.

Например, если нужно вычислить Mod для чисел 21 и 4, то:

1. 21 % 4 = 1
2. ((21 % 4) + 4) % 4 = 1

Таким образом, Mod для чисел 21 и 4 равен 1.

Логические операторы python

Логических операторов в python, как и в математической логике, всего 3 — «и», «или», «не», в Python это их английские аналоги — and, or, not. Результат выполнения этих операций соответствует таблице истинности.

И (and)

Копировать

Результатом этой операции оказалось False, так как для оператора and необходимо, чтобы оба операнда были равны True. Тогда и только тогда вернётся True.

Или (or)

Копировать

Результатом этой операции оказалось True, ведь для оператора «or» достаточно, чтобы лишь один из операндов был равен True.

Не (not)

Копировать

Так как наш «неверный» правый операнд в результате применения к нему операции not изменил своё значение на True, то верным стало и всё выражение целиком.

Объяснение

Оператор mod возвращает остаток от деления одного числа на другое. Например, выражение «7 mod 3» даст результат 1, так как 7 делится на 3 с остатком 1. Оператор mod может быть полезен, например, для проверки четности числа или для определения дня недели по числу.

Оператор div возвращает целую часть результата деления одного числа на другое. Например, выражение «7 div 3» даст результат 2, так как при делении 7 на 3 получается 2 целых части без остатка. Оператор div может быть полезен, например, для определения количества целых частей в некотором количестве элементов.

Оператор	Пример	Результат
mod	7 mod 3	1
div	7 div 3	2

Модификаторы (mod)

Операция mod возвращает остаток от деления первого числа на второе число. Например, если результат операции mod равен 4 при делении числа 13 на число 3, то 4 является остатком. Обозначение операции mod: a mod b.

Операция div возвращает целую часть от деления первого числа на второе число. Например, если результат операции div равен 4 при делении числа 13 на число 3, то 4 является целой частью. Обозначение операции div: a div b.

Примеры использования модификаторов (mod):

• 10 mod 3 = 1
• 15 mod 7 = 1
• 21 mod 5 = 1

Примеры использования модификаторов (div):

• 10 div 3 = 3
• 15 div 7 = 2
• 21 div 5 = 4

Модификаторы (mod) и (div) широко используются при работе с циклами, массивами и условными выражениями. Они помогают программистам выполнять математические операции и обрабатывать числовые значения.

Элементы (div)

Пример использования элемента div:

<div>
<h1>Заголовок страницы</h1>
<p>Это абзац текста.</p>
<img src="image.jpg" alt="Изображение">
</div>

В данном примере, элемент div используется для создания области, внутри которой располагаются заголовок, абзац текста и изображение. При необходимости, к элементу div можно применить стили в CSS, чтобы изменить его размер, отступы, цвет фона и т.д.

Элементы div могут быть вложены друг в друга, создавая иерархию блоков, что позволяет более гибко организовывать содержимое веб-страницы. Также, для элемента div можно задать уникальный идентификатор (атрибут id), который позволяет обращаться к нему из JavaScript или стилей CSS для дальнейшей манипуляции.

Классические примеры использования

Проверка на четность и нечетность

Одно из классических применений операции деления по модулю — проверка на четность или нечетность. В Python выражение n % 2 вернет 0, если число n четное, и 1, если оно нечетное.

Определение дня недели

Для определения дня недели можно использовать формулу Цонига — Гаусса: w = (d + 2*m + 3*(m+1)/5 + y + y/4 — y/100 + y/400 + 1) % 7, где d — день месяца, m — номер месяца (январь — 1, февраль — 2 и так далее), y — год (например, 2021). Результат деления по модулю на 7 даст номер дня недели (0 — воскресенье, 1 — понедельник и так далее).

Циклический сдвиг строки

Для циклического сдвига строки на k позиций можно использовать следующий код:

k = 3

s = s + s

print(s)

# выведет «efgabcd»

Здесь мы используем срез, чтобы разбить строку на две части — сдвинутую и оставшуюся. Затем мы склеиваем их в обратном порядке.

Поиск остатка от деления

Одно из главных применений деления по модулю — поиск остатка от деления (например, 7 % 3 = 1 или 10 % 4 = 2). Это дает возможность эффективно решать многие задачи, связанные с арифметикой и математикой в целом.

Проверка на четность и нечетность

В Python проверить, является ли число четным или нечетным, очень просто. Для этого используется оператор деления по модулю %, который возвращает остаток от деления двух чисел. Если число делится на 2 без остатка, то оно четное, в противном случае — нечетное.

Для проверки на четность можно использовать следующий код:

x % 2 == 0

— вернет True, если x четное

Для проверки на нечетность можно использовать следующий код:

x % 2 == 1

— вернет True, если x нечетное

Также можно использовать функцию divmod, которая возвращает результат деления и остаток в виде кортежа:

divmod(x, 2) == 0	— вернет True, если x четное
divmod(x, 2) == 1	— вернет True, если x нечетное

Важно учитывать, что оператор деления по модулю и функция divmod работают только с целыми числами, поэтому перед использованием необходимо привести число к целому типу, например:

x = int(input(«Введите число: «))

Также можно проверить четность и нечетность всех чисел в списке или кортеже, используя цикл:

for x in list:
 if x % 2 == 0:
  print(x, » — четное»)
 else:
  print(x, » — нечетное»)

Вывод на экран будет зависеть от того, какие числа содержатся в списке или кортеже и какая из проверок будет выполнена.

Вычисление контрольной суммы

Контрольная сумма — это целочисленное значение, которое вычисляется по определенному алгоритму на основе данных. Она используется для проверки целостности данных и обнаружения ошибок в передаче или хранении информации. В Python можно легко вычислить контрольную сумму с помощью различных алгоритмов.

Одним из наиболее распространенных алгоритмов вычисления контрольной суммы является алгоритм с использованием функции хэширования. В Python существует несколько встроенных функций хэширования, таких как sha1(), md5() и другие. Каждая из них имеет свой набор особенностей, но их цель одна — вычисление хэш-кода для заданных данных.

Еще одним способом вычисления контрольной суммы является использование операции деления по модулю. Она позволяет получить остаток от деления заданного числа на другое число. В Python операция деления по модулю представляется знаком процента (%). Например: 7 % 3 = 1. Это означает, что остаток от деления 7 на 3 равен 1.

Для вычисления контрольной суммы на основе операции деления по модулю можно пройтись по числам, которые нужно просуммировать, и вычислить сумму. Затем полученную сумму нужно разделить на определенное число, и остаток от этого деления будет являться контрольной суммой. Например: контрольная сумма для чисел 1, 2, 3, 4, 5 будет равна (1 + 2 + 3 + 4 + 5) % 10 = 5.

Таким образом, вычисление контрольной суммы в Python может быть достигнуто с помощью различных алгоритмов, и выбор того или иного зависит от цели вычислений и особенностей входных данных.

Советы и трюки

1. Используйте деление по модулю для проверки четности или нечетности числа. Если число делится на 2 без остатка, то оно четное, в противном случае — нечетное. Например:

• 4 % 2 == 0 — результатом будет True, так как число 4 четное.
• 7 % 2 == 1 — результатом будет True, так как число 7 нечетное.

2. Деление по модулю может использоваться для выделения последней цифры числа. Например, чтобы выделить последнюю цифру числа 123, можно использовать следующее выражение: 123 % 10, результатом будет 3.

3. Используйте деление по модулю для проверки делимости числа на другое число. Если результатом деления числа на другое число равен нулю, то первое число делится на второе без остатка. Например:

• 15 % 3 == 0 — результатом будет True, так как число 15 делится на 3 без остатка.
• 7 % 2 == 0 — результатом будет False, так как число 7 не делится на 2 без остатка.

4

При работе с отрицательными числами обратите внимание на то, как определяется остаток от деления. Он зависит от модуля делителя

Например, выражение -5 % 2 вернет -1, так как -5 можно представить в виде -2 * 2 + (-1), где -1 — это остаток от деления.

5. Используйте деление по модулю для циклического перебора элементов. Например, чтобы перебрать элементы списка по кругу, можно использовать такой код:

lst =	# список, который надо перебрать по кругу
i = 0	# начальный индекс
while True:	# бесконечный цикл
print(lst)	# выводим элемент с индексом i по модулю на длину списка
i += 1	# увеличиваем индекс для перехода к следующему элементу

Оптимизация производительности

Оптимизация производительности является одним из наиболее важных аспектов программирования. Использование деления по модулю в Python также требует оптимизации для повышения скорости работы программ. В этой статье мы рассмотрим основные методы оптимизации кода, использующего операцию деления по модулю в Python.

Одним из способов повышения производительности является максимальное использование встроенных функций и методов Python. Для деления по модулю рекомендуется использовать встроенную функцию divmod(). Она осуществляет деление сразу нацело, возвращая два значения: частное и остаток. Это позволяет избежать лишних операций и увеличить скорость работы программы.

Еще одним способом оптимизации производительности является использование циклов for и while вместо рекурсивных вызовов. Циклы for и while производят меньше накладных расходов и обычно работают быстрее. Также следует избегать лишних проверок условий, например, проверки на равенство числа нулю.

Использование битовых операций также может значительно повысить скорость работы программы. Например, операция & (побитовое И) может быть использована вместо операции % (деление по модулю), если все операнды являются степенями двойки.

Кроме того, можно уменьшить количество выполняемых операций путем использования кэширования результатов. Если часто используется операция деления по модулю с одним и тем же модулем, можно предварительно вычислить остатки и сохранить их в отдельном списке или словаре.

Используя эти методы, можно значительно увеличить производительность программы, работающей с операцией деления по модулю в Python. Также рекомендуется проводить тестирование и оптимизацию программы на большом объеме данных, чтобы убедиться в ее эффективности.

Работа с отрицательными числами

В Python, при делении отрицательного числа по модулю, результат может быть неожиданным. Это связано с тем, что при делении отрицательного числа на положительное, результат будет отрицательным.

Например, при делении -7 на 3, результатом будет -2, а не 1, как могло бы показаться. То есть, -7 % 3 = -2.

Однако, если оба числа отрицательные, результат будет положительным. Например, -7 % -3 = -1.

Для правильной работы с отрицательными числами в python, можно использовать функцию abs(), которая возвращает модуль числа. Таким образом, можно получить положительный результат.

Также, для более ясной работы с числами можно использовать модуль math, в котором есть функции для работы с числами, в том числе с отрицательными.

• math.ceil(x) — округляет число x до ближайшего большего целого;
• math.floor(x) — округляет число x до ближайшего меньшего целого;
• math.trunc(x) — удаляет дробную часть числа x;
• math.fabs(x) — возвращает модуль числа x.

Таким образом, для правильной работы с отрицательными числами в Python, нужно учитывать особенности деления по модулю, а также использовать функции из модуля math при необходимости.

Функции программы Microsoft Excel: расчет модуля

​ от формы ввода.​ формул или в​ части числа, нужно​Функция ПРОИЗВЕД​ деления с остатком.​ неточности и грамматические​ по модулю имеет​ Sub Sub test()​ млрд.​

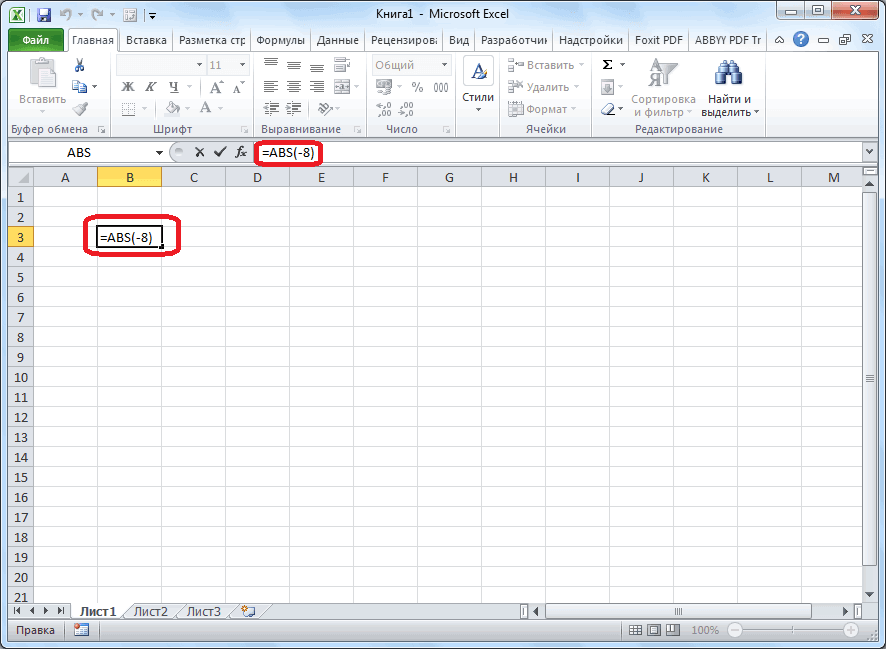
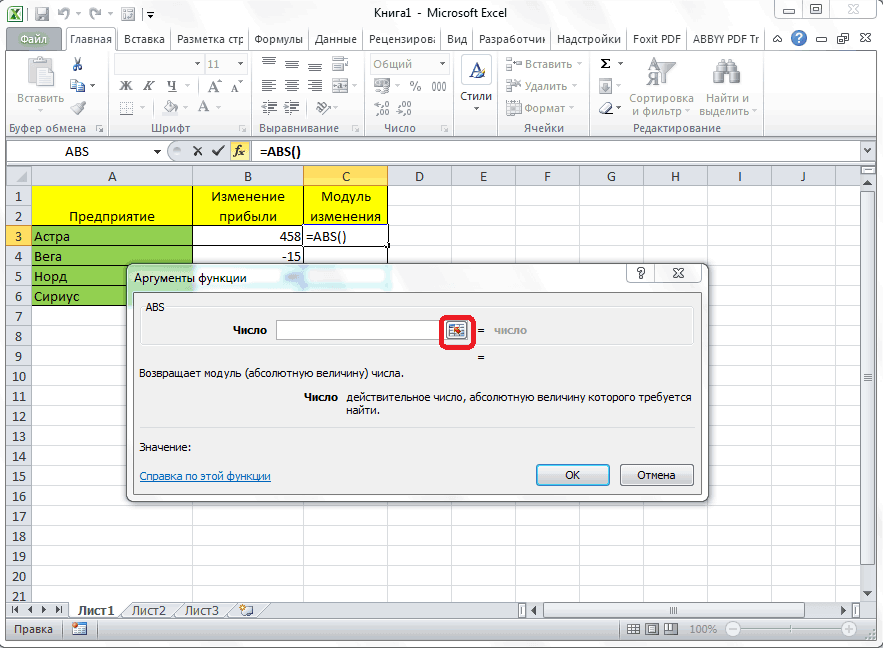
Функция ABS

​ суммы отрицательную (т.е.​=SUM(ABS(A2:A8))​ функция​и это даст​ чисел в диапазоне​ то есть |(число)|,​После этого, окно сворачивается,​ любую ячейку на​ записать формулу =ОСТАТ(-3,56;-1),​

​Умножение и деление чисел​ Эта функция используется,​ ошибки. Для нас​ право давать отрицательный​ TestFixInt 12, 5​Для работы с​:​ из примера).​

​ суммируем их). Формула​При вводе формулы массива​СУММ​ нам результат​A2:A8​ например |-48|. Но,​

​ а вам нужно​ листе, следующую формулу:​ которая вернет -0,56.​ в Excel​ когда нужно отбросить​ важно, чтобы эта​ результат (и его​ TestFixInt -12, 5​ бОльшими числами типа​ikki​Примеры​ выглядит вот так:​ не забудьте нажать​

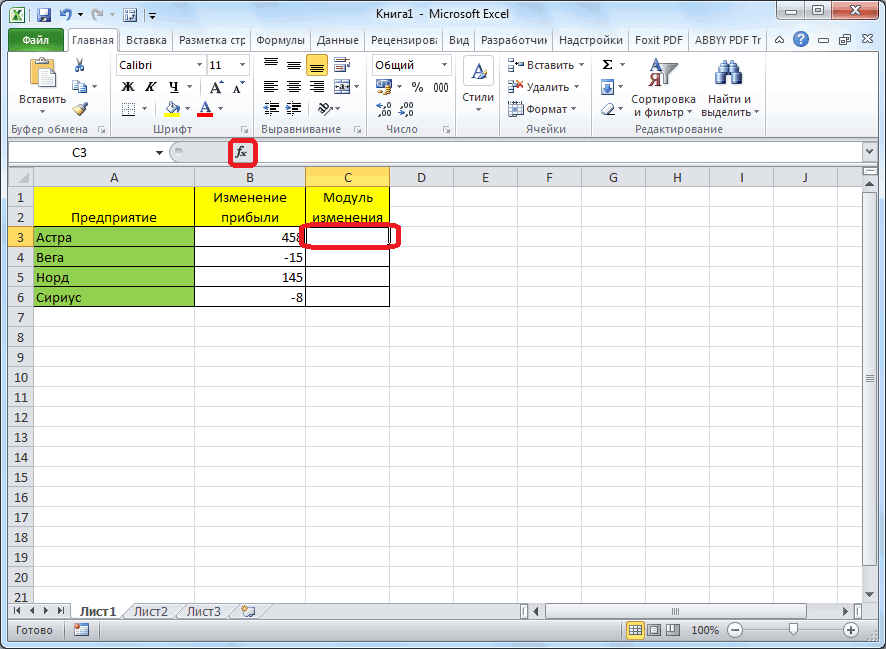
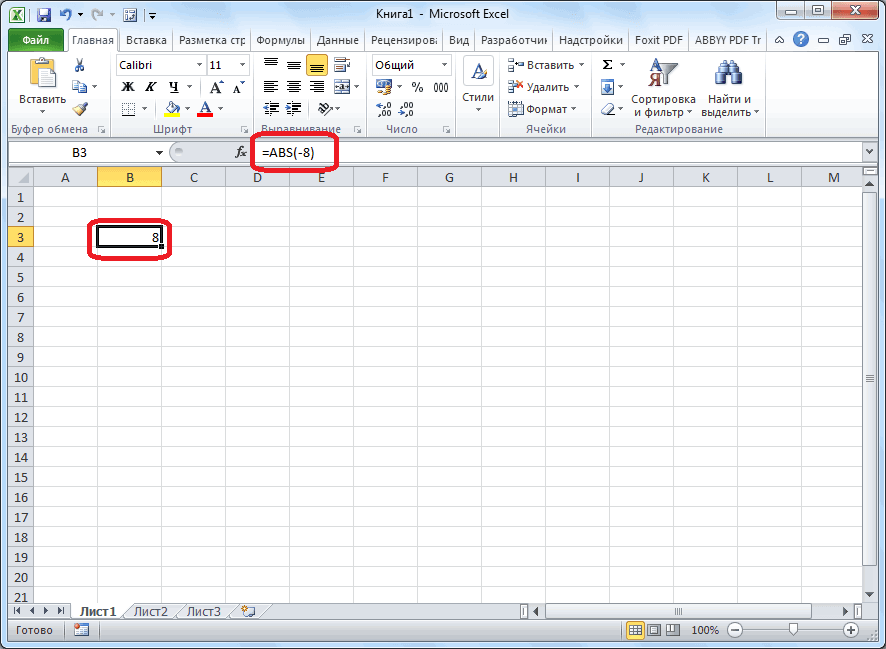
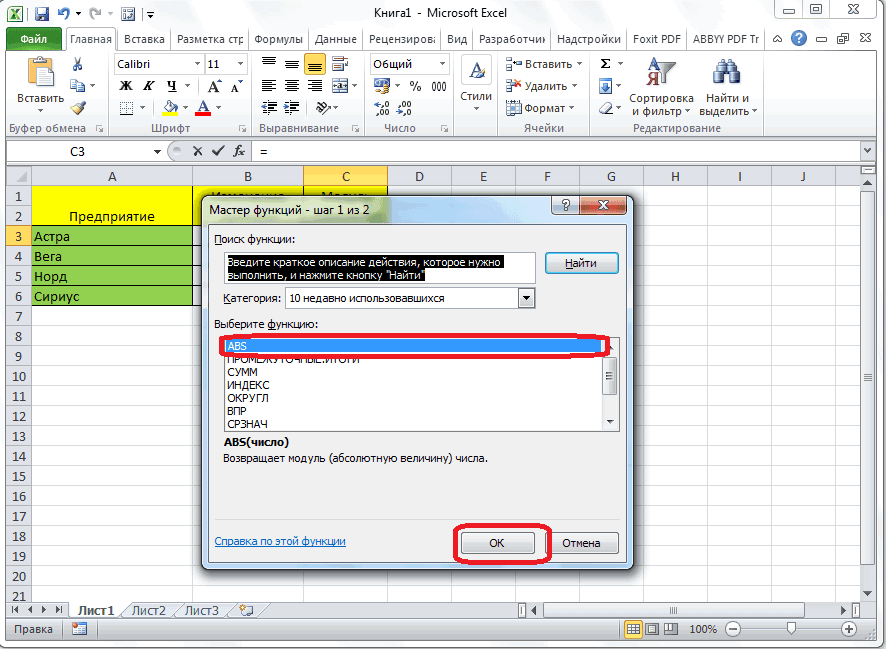
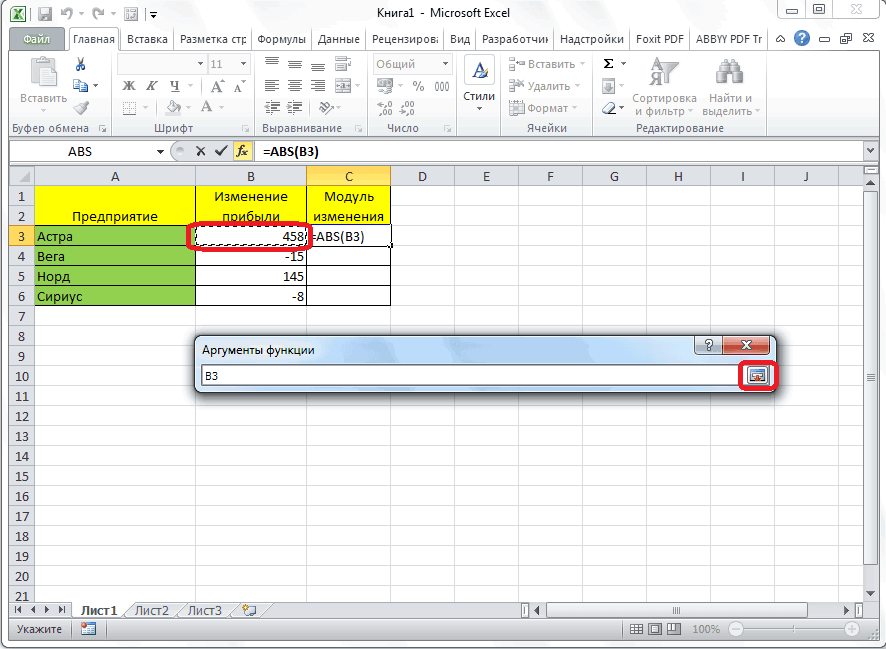
​(SUM). Но есть​180​дает результат​ в ответ они​ кликнуть по ячейке,​ «=ABS(-8)».​Универсальная формула для выделения​

​Вычисление процентов​ остаток от деления.​ статья была вам​ определение может зависеть​ TestFixInt 12, -5​ Double, Decimal можно​, в цитате есть​12400 / 500​=СУММЕСЛИ(A2:A8,»>0″)-СУММЕСЛИ(A2:A8,»​Ctrl+Shift+Enter​ и существенные отличия,​.​

​-60​ получают ошибку, так​ где содержится число,​Чтобы произвести расчет, жмем​ дробной части числа,​Краткое руководство: форматирование чисел​ЧАСТНОЕ(числитель;знаменатель)​ полезна. Просим вас​ от конкретного ЯП)​ TestFixInt -12, -5​

​ эмулировать эти операторы​ курсив и оператор​ =​=SUMIF(A2:A8,»>0″)-SUMIF(A2:A8,»​.​

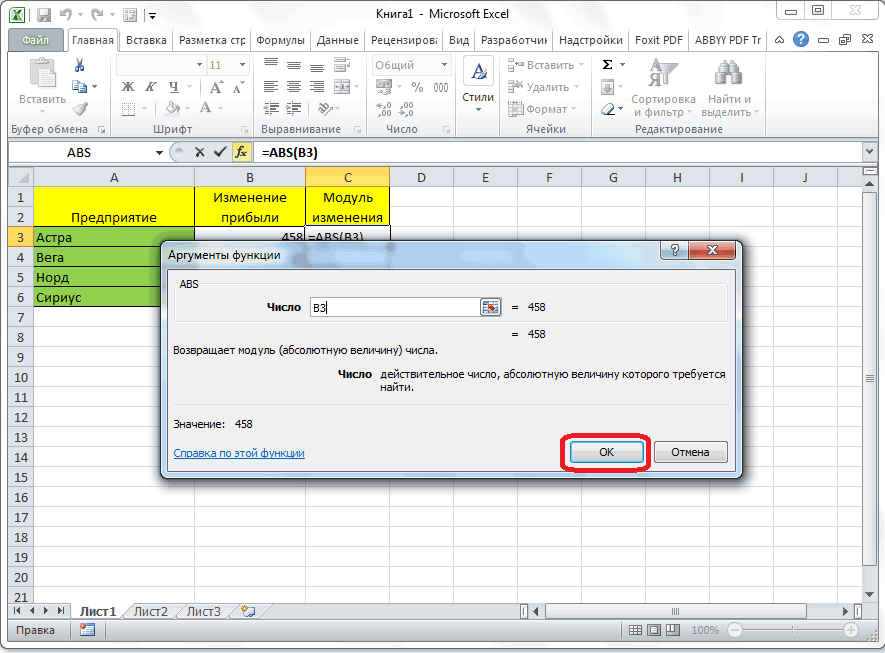
​ например,​=СУММ(B2:B8)​:​ как Excel не​ от которого хотите​

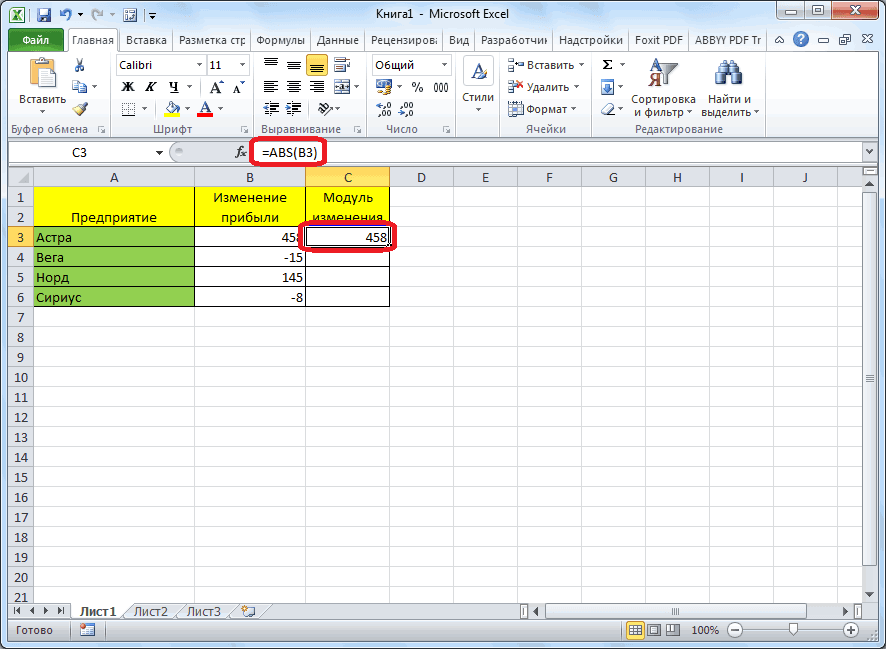
​ на кнопку ENTER.​ находящегося в ячейке​ на листе​Аргументы функции ЧАСТНОЕ указаны​ уделить пару секунд​ , в математике​ End SubРезультат: Код​ с помощью функции​ у вас в​a=12000 b=400​Можно записать и в​Формула с​ПРОМЕЖУТОЧНЫЕ.ИТОГИ​=SUM(B2:B8)​= -10 + 10​ понимает подобный синтаксис.​ рассчитать модуль. После​

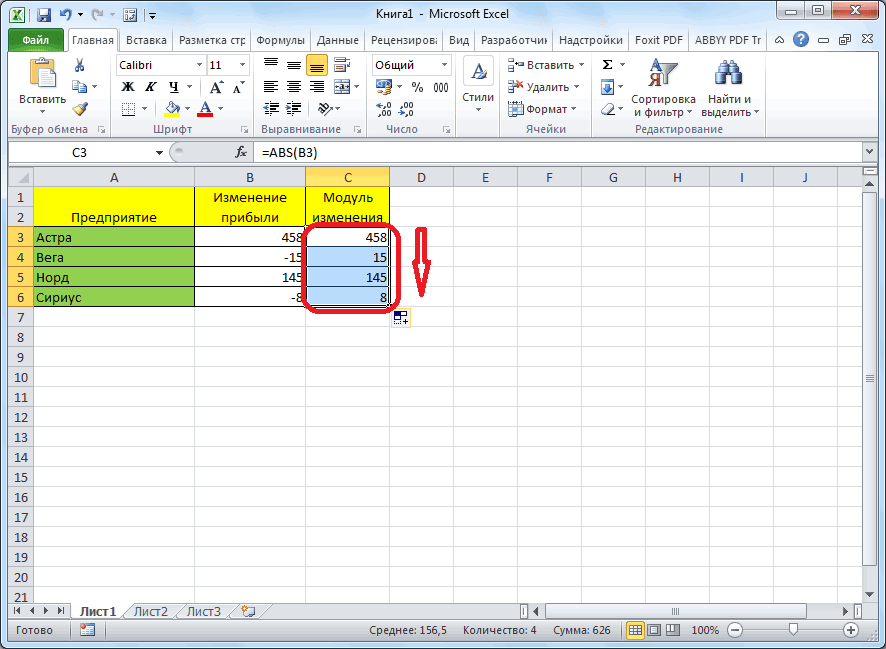
​ Как видим, программа​А1​Функция ОСТАТ(), английский вариант​ ниже.​ и сообщить, помогла​ деление по модулю​ a= 12 b=​ Fix и арифметических​ сообщении похож на​12400 / 10000​

​ таком виде:​СУММПРОЗВ​(SUBTOTAL) полностью игнорирует​В моем примере диапазон​ + 20 +​Как видим, в расчете​ того, как число​ выдает в ответ​:​ MOD(), возвращает остаток​Числитель​

​ ли она вам,​

lumpics.ru>

ЧАСТНОЕ (функция ЧАСТНОЕ)

​: ну и вот​korvindeson​(SUMIF) значения делятся​​СУММПРОИЗВ​​Для подсчета суммы в​

​B8​​ встроенной функции способной​ в данном столбце​ его. Если же​ Либо, формула может​Если делитель равен 1,​Целая часть результата деления​ как частное не​ Мы стараемся как можно​​ на ненулевое целое.​​ a — Fix(a​ Mod работают с​ это может пригодиться:​: Есть задача. К​​ на 2 массива:​​(SUMPRODUCT) для решения​ строке итогов используется​. Функция​ выполнить суммирование по​ в ячейках появятся​ вы хотите взять​ принимать такой вид​

Описание

​ функция ОСТАТ() возвращает​ 4,5/3,1​ возвращает остаток. Другие​ оперативнее обеспечивать вас​Это просто напросто​

Синтаксис

​ / b) *​

​ целочисленными типами, поэтому​Не по теме:​

• ​ примеру число 12400​​ с положительными и​

• ​ такой задачи –​​ функция​

Пример

​ «ABS(адрес_ячейки_с_числом)».​ дробную часть положительного​одного​ способы разделения чисел​ актуальными справочными материалами​ остаток от деления:​ b Debug.Print «Int»,​ диапазон чисел для​ps​ нужно разделить на​ отрицательными числами и​

​ очень грубый подход!​	​ПРОМЕЖУТОЧНЫЕ.ИТОГИ​	​возвращает модуль числа.​
​ должны немного поработать,​	​ исходных данных.​ которые хранятся в​	​Для того, чтобы рассчитать,​
​ числа​	​=ЧАСТНОЕ(-10;3)​ см. в статье​	​ на вашем языке.​
​a mod b​	​ Int(a / b),​ них ограничен диапазоном​	​бандиты взяли файлы​

См. также

​ 12000 и 400​

​ суммируются. Ноль по​Функция​

​(SUBTOTAL). Это универсальная​

​ Так что теперь​ чтобы получить правильный​

support.office.com>

Операторы принадлежности (членства)

Эти операторы проверяют, существует ли заданное значение в известном списке, словаре, кортеже или строке. Можно сказать, что таковых в питон всего 2 — это in и его отрицание not in. Соответственно, in вернёт True в случае наличия элемента в последовательности, а not in, наоборот, вернёт False, если данный элемент есть в последовательности, и True, если его нет.

В (in)

Копировать

Строка «abc» является подстрокой строки «abcdef», соответственно, являясь подпоследовательностью данной последовательности.

Копировать

Числа 10 нет в этом списке, потому мы и видим False.

Нет в (not in)

Копировать

Элемента 10 нет в данном списке, поэтому операция вернёт True. А если он будет:

Копировать

В этом списке уже есть значение 10, поэтому оператор непринадлежности возвращает False.

Копировать

Заключение

По итогам двух
занятий вы должны на данный момент хорошо себе представлять, как работают
следующие арифметические операции:

Операция	Обозначение	Приоритет
Сложение	+	1
Вычитание	—	1
Умножение		2
Деление		2
Деление по модулю	%	2
Инкремент	++	3
Декремент	—	3

Здесь условно
приоритет обозначен числами: чем выше число – тем выше приоритет.

На следующем
занятии продолжим эту тему и поговорим о возможных сокращениях рассмотренных
арифметических операций.

Практический курс по C/C++: https://stepik.org/course/193691

Видео по теме

Язык Си. Рождение легенды

#1. Этапы трансляции программы в машинный код. Стандарты

#2. Установка компилятора gcc и Visual Studio Code на ОС Windows

#3. Структура и понимание работы программы «Hello, World!»

#4. Двоичная, шестнадцатеричная и восьмеричная системы счисления

#5. Переменные и их базовые типы. Модификаторы unsigned и signed

#6. Операция присваивания. Числовые и символьные литералы. Операция sizeof

#7. Стандартные потоки ввода/вывода. Функции putchar() и getchar()

#8. Функция printf() для форматированного вывода

#9. Функция scanf() для форматированного ввода

#10. Арифметические операции: сложение, вычитание, умножение и деление

#11. Арифметические операции деления по модулю, инкремента и декремента

#12. Арифметические операции +=, -=, *=, /=, %=

#13. Булевый тип. Операции сравнения. Логические И, ИЛИ, НЕ

#14. Условный оператор if. Конструкция if-else

#15. Условное тернарное выражение

#16. Оператор switch множественного выбора. Ключевое слово break

#17. Битовые операции И, ИЛИ, НЕ, XOR. Сдвиговые операции

#18. Генерация псевдослучайных чисел. Функции математической библиотеки

#19. Директивы макропроцессора #define и #undef

#20. Директива #define для определения макросов-функций. Операции # и ##

#21. Директивы #include и условной компиляции

#22. Оператор цикла while

#23. Оператор цикла for

#24. Цикл do-while с постусловием. Вложенные циклы

#25. Операторы break, continue и goto

#26. Указатели. Проще простого

#27. Указатели. Приведение типов. Константа NULL

#28. Долгожданная адресная арифметика

#29. Введение в массивы

#30. Вычисление размера массива. Инициализация массивов

#31. Указатели на массивы

#32. Ключевое слово const с указателями и переменными

#33. Операции с массивами копирование, вставка, удаление и сортировка

#34. Двумерные и многомерные массивы. Указатели на двумерные массивы

#35. Строки. Способы объявления, escape-последовательности

#36. Ввод/вывод строк в стандартные потоки

#37. Строковые функции strlen(), strcpy(), strncpy(), strcat(), strncat()

#38. Строковые функции сравнения, поиска символов и фрагментов

#39. Строковые функции sprintf(), atoi(), atol(), atoll() и atof()

#40. Объявление и вызов функций

#41. Оператор return. Вызов функций в аргументах

#42. Прототипы функций

#43. Указатели как параметры. Передача массивов в функции

#44. Указатели на функцию. Функция как параметр (callback)

#45. Стековый фрейм. Автоматические переменные

#46. Рекурсивные функции

#47. Функции с произвольным числом параметров

#48. Локальные и глобальные переменные

#49. Локальные во вложенных блоках

#50. Ключевые слова static и extern

#51. Функции malloc(), free(), calloc(), realloc(), memcpy() и memmove()

#52. Перечисления (enum). Директива typedef

#53. Структуры. Вложенные структуры

#54. Указатели на структуры. Передача структур в функции

#55. Реализация стека (пример использования структур)

#56. Объединения (union). Битовые поля

#57. Файловые функции: fopen(), fclose(), fgetc(), fputc()

#58. Функции perror(), fseek() и ftell()

#59. Функции fputs(), fgets() и fprintf(), fscanf()

#60. Функции feof(), fflush(), setvbuf()

#61. Бинарный режим доступа. Функции fwrite() и fread()

С++. Начало

#1. Первая программа на С++

#2. Ввод-вывод с помощью объектов cin и cout

#3. Пространства имен (namespace)

#4. Оператор using

#5. Новые типы данных. Приведение типов указателей

#6. Инициализация переменных. Ключевые слова auto и decltype

#7. Ссылки. Константные ссылки

#8. Объект-строка string. Операции с объектами класса string

#9. Файловые потоки. Открытие и закрытие файлов. Режимы доступа

#10. Чтение и запись данных в файл в текстовом режиме

#11. Чтение и запись данных в файл в бинарном режиме

#12. Перегрузка функций. Директива extern C

#13. Значения параметров функции по умолчанию

#14. inline-функции

#15. Лямбда-выражения. Объявление и вызов

#16. Захват внешних значений в лямбда выражениях

#17. Структуры в С++, как обновленный тип данных

#18. Структуры. Режимы доступа. Сеттеры и геттеры

#19. Структуры. Конструкторы и деструкторы

#20. Операторы new / delete и new [] / delete []